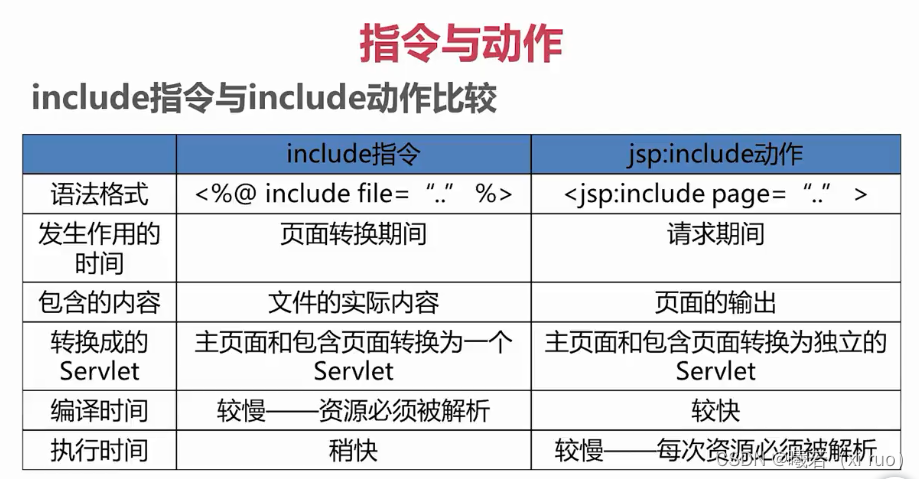
图像处理之SVD检测显示屏缺陷（C++）

---

---

前言

显示屏缺陷检测是机器视觉领域的一处较广泛的应用场景，显示屏主要有LCD和OLED，缺陷类型主要包括点线缺陷（亮暗点，亮暗线），Mura缺陷（亮度显示不均），外观缺陷（划伤，破损，脏污）等。

SVD（奇异值分解）算法主要用于图像的降维和重构，图像重构一般是取前k个较大的奇异值，其他值置为0，滤除干扰噪声从而实现图像重构；而论文作者反其道而行，令前k个奇异值为0进行图像重构，用于凸显图片中的各类缺陷，达到缺陷检测的目的。

根据SVD的算法原理，较大奇异值包含图像主要特征，而较小奇异值包含噪声信息，在实验中发现，重构图片中，除了凸显出Mura缺陷外，还包含很多雪花状噪声；随着k值的增大，当k值超过一个阈值后，重构图片中Mura缺陷将会消失；故，我们可以将奇异值矩阵分为3部分：包含图像主要特征的较大奇异值，包含缺陷特征的相对较大奇异值，包含噪声特征的较小奇异值，将较大奇异值和较小奇异值都置零，只保留相对较大奇异值，以此重构图像，在图像缺陷信息基础上同时做去噪处理。

参考资料：
Lu, CJ., Tsai, DM. Automatic defect inspection for LCDs using singular value decomposition. AMT 25, 53–61 (2005). https://doi.org/10.1007/s00170-003-1832-6
反向应用SVD（奇异值分解）算法检测显示屏缺陷
反向应用SVD（奇异值分解）算法检测显示屏缺陷(续)

---

一、SVD算法简介

一整张图片就是一个像素值矩阵，每个像素值0-255之间，SVD可以把一个矩阵分解成左奇异向量矩阵U、奇异值矩阵 Σ（S）和右奇异向量矩阵VT

正交矩阵U：m行m列，该矩阵的每一个列向量都是AAT的特征向量；
正交矩阵VT：n行n列，该矩阵的每一个列向量都是ATA的特征向量；
对角阵Σ：m行n列，将ATA或AAT的特征值开根号，得到的就是该矩阵主对角线上的元素，也可以看成矩阵A的奇异值。

二、代码实现

#include <iostream>
#include <opencv.hpp>
using namespace std;
using namespace cv;

#define R 0.3
#define G -0.03

/*
* @param cv::Mat S	 特征值集合
* @param int	 k	 上限
* @param int	 l	 下限
* @brief 根据经验公式计算k和l
*/
void get_k_l(const cv::Mat& S, int& k, int& l)
{
	cv::Mat S_ = S.clone();
	//求特征值的平均值和方差
	cv::Mat meanMat, stdMat;
	cv::meanStdDev(S, meanMat, stdMat);

	for (int i = 0; i < S.rows; i++)
	{
		S_.at<float>(i, 0) = (S_.at<float>(i, 0) - meanMat.at<double>(0)) / stdMat.at<double>(0);
	}

	//计算k
	for (int i = 0; i < S.rows; i++)
	{
		if (S_.at<float>(i, 0) < R)
		{
			k = i;
			break;
		}
	}

	//计算g
	for (int i = 0; i < S.rows; i++)
	{
		if (S_.at<float>(i, 0) < G)
		{
			l = i;
			break;
		}
	}
}

/*
* @param cv::Mat src 输入图像(单通道灰度图像)
* @param cv::Mat dst 输出图像
* @param int	 k	 上限
* @param int	 l	 下限
* @param bool 	 cal	true--自动计算，只需修改G\R;false--手动指定k和l
* @brief svd分解
*/
void svd(const cv::Mat& src, cv::Mat& dst,int k,int l,bool cal)
{
	cv::Mat src_ = src.clone();
	src_.convertTo(src_, CV_32FC1);
	cv::Mat U, S, Vt;
	cv::SVD::compute(src_, S, U, Vt);	//SVD分解
	// S是n行1列(CV_32F);U是m行n列(CV_32F);Vt是n行n列(CV_32F)

	//自动计算
	if(cal) get_k_l(S, k, l);
	if (k < 0)
	{
		cout << "k should larger than 0";
		return;
	}

	if (l <= k)
	{
		cout << "l should larger than k";
		return;
	}

	int min_dim = min(src.rows, src.cols);

	cv::Mat S_(min_dim, min_dim, CV_32FC1, cv::Scalar(0));
	for (int i = k; i <= l; i++)
	{
		S_.at<float>(i, i) = S.at<float>(i, 0);
	}

	cv::Mat result = U * S_ * Vt;
	result.convertTo(dst, CV_8UC1);
}

int main()
{
	string path = "F://work_study//algorithm_demo//";
	cv::Mat src = cv::imread(path + "lena.jpg", cv::IMREAD_GRAYSCALE);
	if (src.empty())
		return -1;


	cv::Mat dst;
	svd(src, dst, 10, 20,true);

	imshow("dst", dst);
	cv::waitKey(0);
	return 0;
}

---

总结

本文主要介绍了SVD分解在图像重构、缺陷检测的应用，使用C++基于OpenCV库实现。
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
该算法的特征值性质有点类似频率域的高频、低频、中频等，欢迎大家交流。
本文代码均在本地运行成功，有问题多交流。