算法学习(6)-最短路径

news2025/1/13 15:34:59

目录

Floyd-Warshall算法

Dijkstra算法

Bellman-Ford算法

Bellman-Ford的队列优化

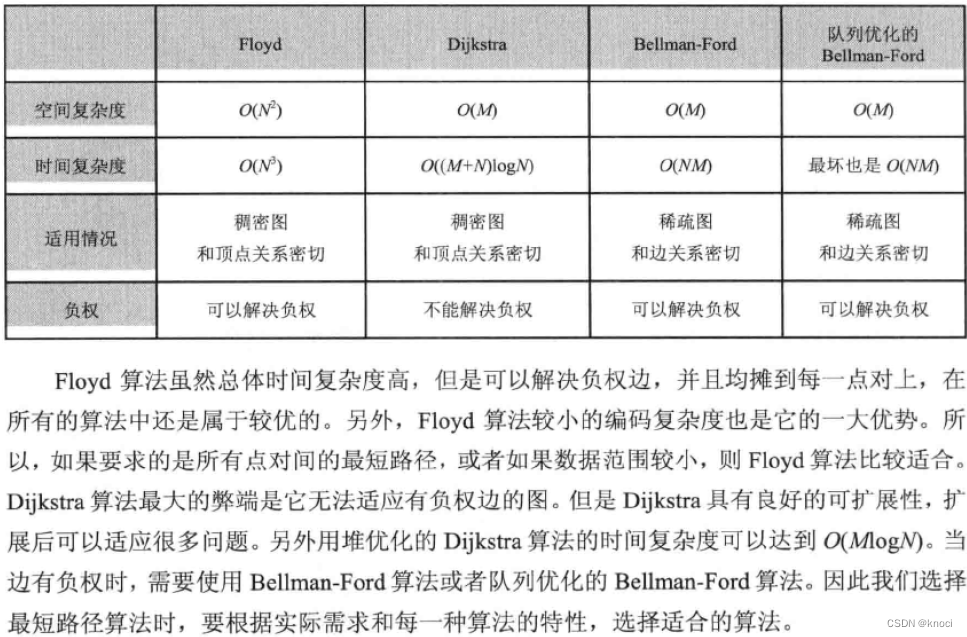
最短路径算法对比分析

Floyd-Warshall算法

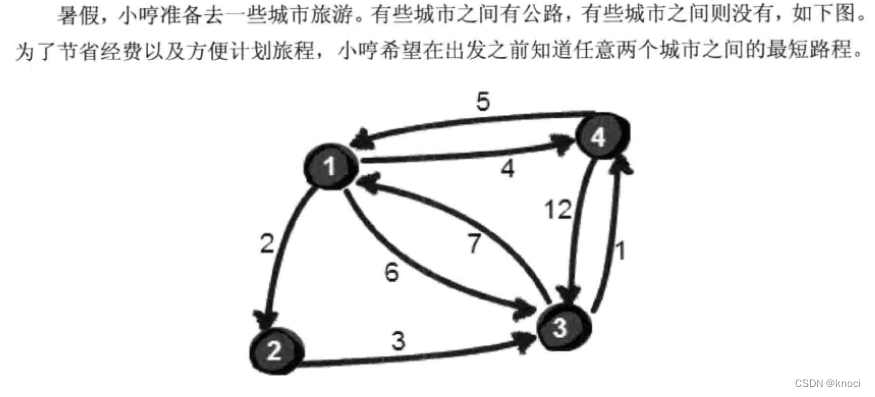
         现在回到问题：如何求任意两点之间的最短路径呢？

        通过之前的学习， 我们知道通过深度或广度优先搜索可以求出两点之间的最短路径。所以进行n^2遍深度或广度优先搜索， 即对每两个点都进行一次深度或广度优先搜索， 便可以求得任慈两点之间的最短路径。可是还有没有别的方法呢？

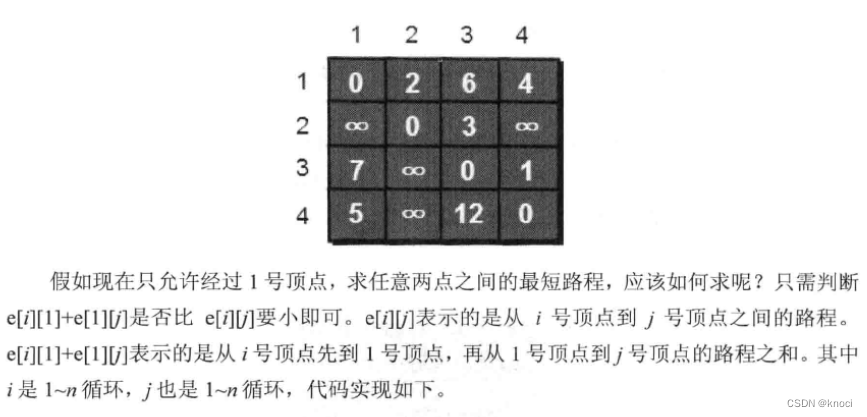
        当任意两点之间不允许经过第三个点时， 这些城市之间的最短路程就是初始路程，如下。

for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++) {
        if (e[i][j] > e[i][1] + e[1][j]) {
            e[i][j] = e[i][1] + e[1][j];
        }
    }
}

        接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢？我们需要在只允许经过 1 号顶点时任意两点的最短路程的结果下， 再判断如果经过 2 号顶点是否可以使得 i 号顶点到 j 号顶点之间的路程变得更短，即判断 e[i][2] + e[2][j] 是否比 e[i][j] 要小，代码实现如下。

//经过1号顶点
for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++) {
        if (e[i][j] > e[i][1] + e[1][j]) {
            e[i][j] = e[i][1] + e[1][j];
        }
    }
}

//经过2号顶点
for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++) {
        if (e[i][j] > e[i][2] + e[2][j]) {
            e[i][j] = e[i][2] + e[2][j];
        }
    }
}

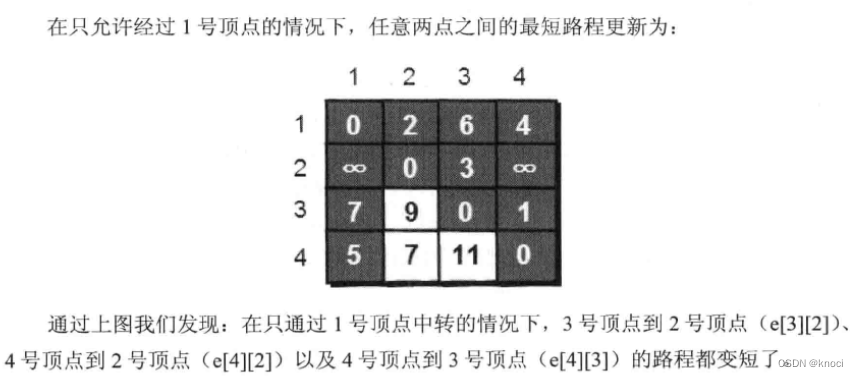
        在只允许经过1 和2号顶点的情况下， 任意两点之间的最短路程更新为：

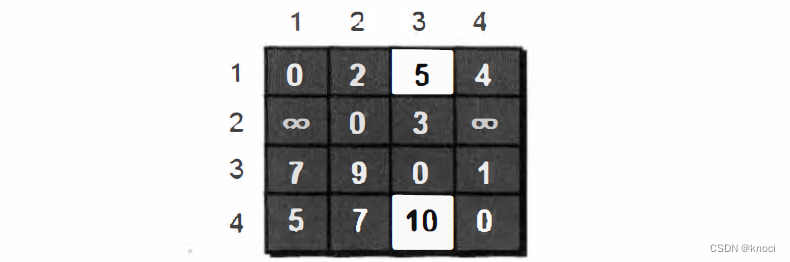
        通过上图得知，在相比只允许通过1号顶点进行中转的情况下，这里允许通过1和2号顶点进行中转， 使得 e[1][3] 和 e[4][3] 的路程变得更短了。
        同理， 继续在只允许经过1 、2和3号顶点进行中转的情况下，求任意两点之间的最短路程。任意两点之间的最短路程更新为： 

        最后允许通过所有顶点作为中转， 任意两点之间最终的最短路程为： 

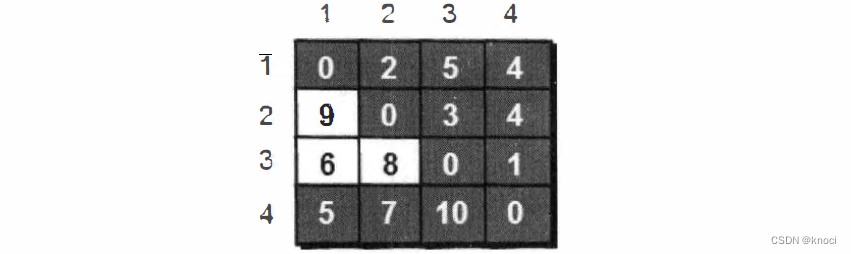
        整个算法过程虽然说起来很麻烦，但是代码实现却非常简单，核心代码只有五行:

for (k = 1; k <= n; k++) {
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            if (e[i][j] > e[i][k] + e[k][j]) {
                e[i][j] = e[i][k] + e[k][j];
            }
        }
    }
}

        这段代码的基本思想就是： 最开始只允许经过1号顶点进行中转， 接下来只允许经过1号和2号顶点进行中转...…允许经过l~n号所有顶点进行中转， 求任意两点之间的最短路程。用一句话概括就是： 从 i 号顶点到 j 号顶点只经过前 k 号点的最短路程。其实这是一种“ 动态规划” 的思想。下面给出这个算法的完整代码：

#include <stdio.h>

int main() {
    int e[10][10], k, i, j, n, m, tl, t2, t3;
    int inf = 99999999; // 用inf (infinity的缩写）存储一个我们认为的正无穷值

    // 读入n和m, n表示顶点个数， 呻畟示边的条数
    scanf("%d %d", &n, &m);

    // 初始化
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            if (i == j)
                e[i][j] = 0;
            else
                e[i][j] = inf;
        }
    }

    // 读入边
    for (i = 1; i <= m; i++) {
        // 第6章最短路径
        scanf("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    // Floyd-Warshall算法核心语句
    for (k = 1; k <= n; k++) {
        for (i = 1; i <= n; i++) {
            for (j = 1; j <= n; j++) {
                if (e[i][j] > e[i][k] + e[k][j])
                    e[i][j] = e[i][k] + e[k][j];
            }
        }
    }

    // 输出朵终的结果
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            printf("%10d", e[i][j]);
        }
        printf("\n");
    }
    return 0;
}

        此算法由RobertW. Floyd（罗伯特·弗洛伊德）千1962年发表在Communications of the ACM上。同年Stephen Warshall（史蒂芬·沃舍尔）也独立发表了这个算法。Robert W. Floyd原本在芝加哥大学读的文学， 但是因为当时美国经济不太景气， 找工作比较困难， 无奈之下到西屋电气公司当了一名计算机操作员， 在IBM650机房值夜班， 并由此开始了他的计算机生涯。此外他还和J.W.J. Williams（威廉姆斯）于1964年共同发明了著名的堆排序算法HEAPSORT。Robert W. Floyd在1978年获得了图灵奖。

Dijkstra算法

         完整的 Dijkstra 算法代码如下：

#include <stdio.h>

int main() {
    int e[10][10], dis[10], book[10], i, j, n, m, t1, t2, t3, u, v, min;
    int inf = 99999999; // 用inf (infinity的缩写）存储一个我们认为的正无穷值

    // 读入n和m, n表示顶点个数， 咕贬瓦边的条数
    scanf("%d %d", &n, &m);

    // 初始化
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            if (i == j)
                e[i][j] = 0;
            else
                e[i][j] = inf;
        }
    }

    // 读入边
    for (i = 1; i <= m; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    // 初始化dis数组， 这里是1号顶点到其余各个顶点的初始路程
    for (i = 1; i <= n; i++) {
        dis[i] = e[1][i];
    }

    // book数组初始化
    for (i = 1; i <= n; i++) {
        book[i] = 0;
    }
    book[1] = 1;

    // Dijkstra算法核心语句
    for (i = 1; i <= n - 1; i++) {
        //找到离1号顶点最近的顶点
        min = inf;
        for (j = 1; j <= n; j++) {
            if (book[j] == 0 && dis[j] < min) {
                min = dis[j];
                u = j;
            }
        }
        book[u] = 1;
        for (v = 1; v <= n; v++) {
            if (e[u][v] < inf) {
                if (dis[v] > dis[u] + e[u][v]) {
                    dis[v] = dis[u] + e[u][v];
                }
            }
        }
    }

    // 输出最终的结果
    for (i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    getchar();
    getchar();
    return 0;
}

        通过上面的代码我们可以看出， 这个算法的时间复杂度是O(N2)。其中每次找到离1号顶点最近的顶点的时间复杂度是O (N), 这里我们可以用“堆”（将在下一章学到）来优化，使得这一部分的时间复杂度降低到O(logN)。另外对于边数M少于N^2的稀疏图来说（我们把M远小于N^2的图称为稀疏图， 而M相对较大的图称为稠密图）， 我们可以用邻接表来代替邻接矩阵， 使得整个时间复杂度优化到O(M+N)logN。请注意！在最坏的情况下M就是N^2， 这样的话(M+N)logN要比N^2还要大。但是大多数情况下并不会有那么多边， 因此(M+N)logN要比N^2小很多。

        现在用邻接标来存储这个图，先给出代码如下：

int n, m, i;
// u、v和w的数组大小要根据实际情况来设置，要比m的最大值要大1
int u[6], v[6], w[6];
//first和next的数组大小要根据实际情况来设置，要比n的最大值要大1
int first[5], next[5];
scanf("%d %d", &n, &m);
//初始化first数组下标1~n的值为-1，表示1~n顶点暂时没有边
for (i = 1; i <= n; i++) {
    first[i] = 1;
}
for (i = 1; i <= m; i++) {
    scanf("%d %d %d", &u[i], &v[i], &w[i]); // 读入每一条边
    //下面两句是关键
    next[i] = first[u[i]];
    first[u[i]] = i;
}

k = first[1];
while(k != -1) {
    printf("%d %d %d\n", u[k], v[k], w[k]);
    k = next[k];
}

        不难发现， 此时遍历某个顶点的边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都是直接插入“ 链表” 的首部而不是尾部。不过这并不会产生任何问题， 这正是这种方法的奇妙之处。遍历每个顶点的边， 其代码如下。

for (i = 1; i <= n; i++) {
    k = first[i];
    while(k != -1) {
        printf("%d %d %d\n", u[k], v[k], w[k]);
        k = next[k];
    }
}

        可以发现使用邻接表来存储图的时间空间复杂度是O(M)， 遍历每一条边的时间复杂度也是O(M)。如果一个图是稀疏图的话， M要远小于N^2。因此稀疏图选用邻接表来存储要比用邻接矩阵来存储好很多。
        最后， 本节介绍的求最短路径的算法是一种基千贪心策略的算法。每次新扩展一个路程最短的点， 更新与其相邻的点的路程。当所有边权都为正时， 由千不会存在一个路程更短的没扩展过的点， 所以这个点的路程永远不会再被改变， 因而保证了算法的正确性。不过根据这个原理， 用本算法求最短路径的图是不能有负权边的， 因为扩展到负权边的时候会产生更短的路程， 有可能就破坏了已经更新的点路程不会改变的性质。既然用这个算法求最短路径的图不能有负权边， 那有没有可以求带有负权边的指定顶点到其余各个顶点的最短路径算法呢？请看下一节。
        最后说一下， 这个算法的名字叫做Dijkstra。该算法是由荷兰计算机科学家Edsger Wybe Dijkstra于1959年提出的。其实这个算法Edsger Wybe Dijkstra在1956年就发现了， 当时他正与夫
人在一家咖啡厅的阳台上晒太阳喝咖啡。因为当时没有专注千离散算法的专业期刊， 直到1959年， 他才把这个算法发表在Numerische Mathematik的创刊号上。

Bellman-Ford算法

        Dijkstra算法虽然好， 但是它不能解决带有负权边（边的权值为负数）的图。本节我要来介绍一个无论是思想上还是代码实现上都堪称完美的最短路算法： Bellman-Ford。Bellman-Ford算法非常简单， 核心代码只有4行， 并且可以完美地解决带有负权边的图， 先来看看它长啥样：

for (k = 1; k <= n-1 k++) {
    for (i = 1; i <= m; i++) {
        if (dis[v[i] > dis[u[i] + w[i]) {
            dis[v[i]] = dis [u[i]] + w[i];
        }
    }
}

if (dis[v[i]] > dis[u[i]] + w[i]) {
    dis[v[i]] = dis[u[i]] + w[i];
}

for (i = 1; i <= m; i++) {
    if (dis[v[i]] > dis[u[i]] + w[i]) {
        dis[v[i]] = dis[u[i]] + w[i];
}

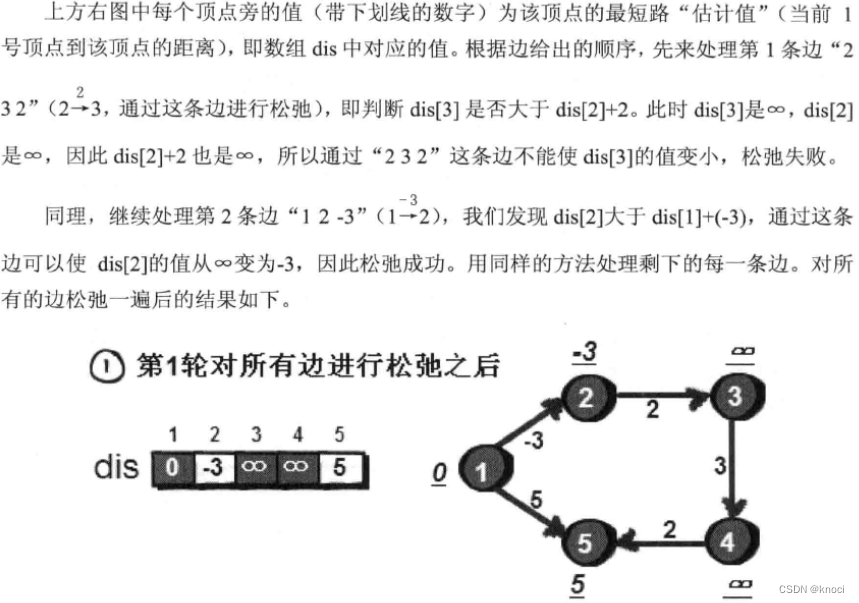
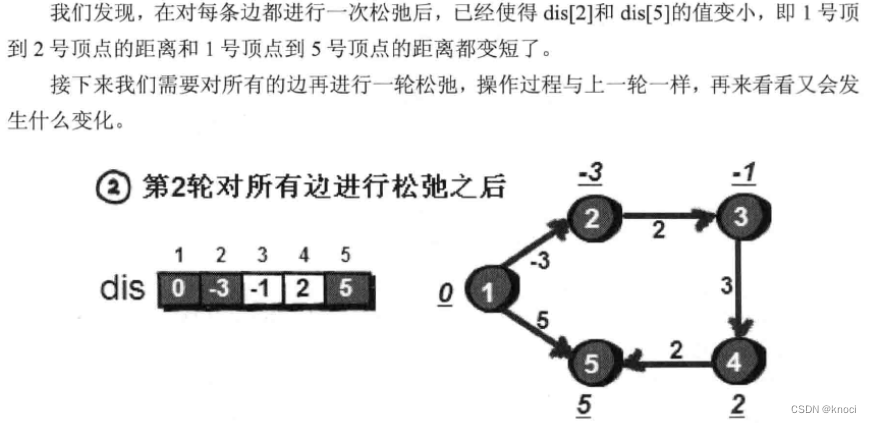
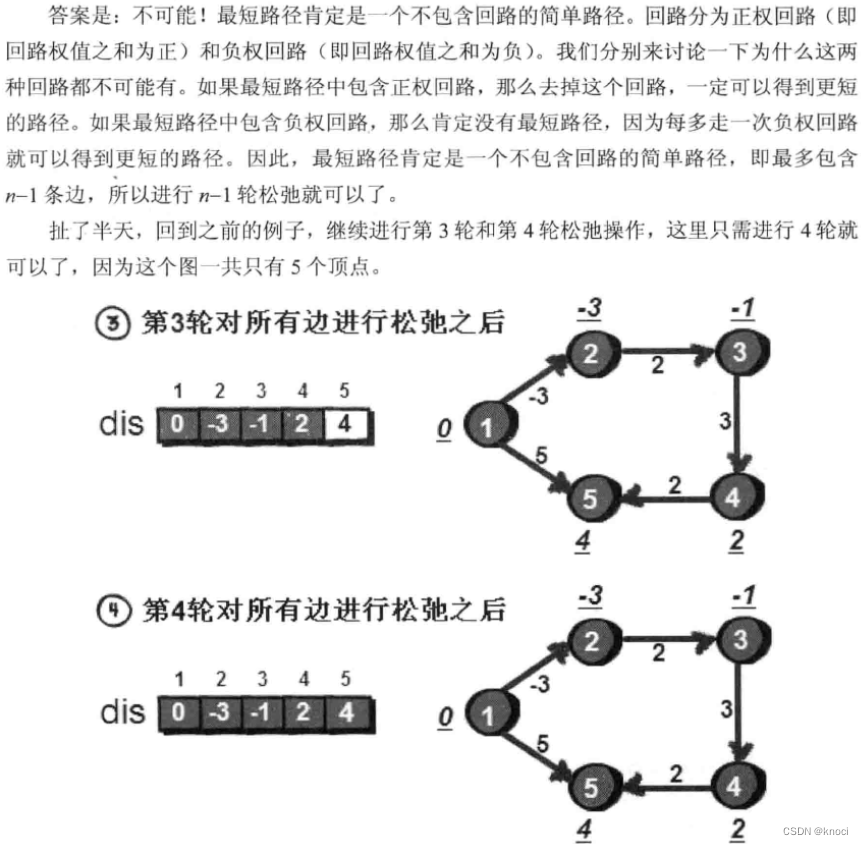
for (k = 1; k <= n-1; k++) { //进行n-1轮松弛
    for (i = 1; i <= m; i++) { //枚举每一条边
        if (dis[v[i]] > dis[u[i]] + w[i]) { //尝试对每一条边进行松弛
            dis[v[i]] = dis[u[i]] + w[i];
        }
    }
}

#include <stdio.h>
int main() {
    int dis[10], i, k, n, m, u[10], v[10], w[10];
    int inf = 99999999;//用inf存储我们认为的无穷大
    //读入n和m, n表示顶点个数，m表示边的条数
    scanf("%d %d", &n, &m);
    
    //读入边
    for (i = 1; i <= m; i++) {
        scanf("%d %d %d", &u[i], &v[i], &w[i]);
    }
    //初始化dis数组，这里是1号顶点到其余各个顶点的初始路程
    for (i = 1; i <= n; i++) {
        dis[i] = inf;
    }
    dis[1] = 0;
    
    //Bellman-Ford算法核心语句
    for (k = 1; k <= n-1; k++) {
        for (i = 1; i <= m; i++) {
            if (dis[v[i]] > dis[u[i]] + w[i]) {
                dis[v[i]] = dis[u[i]] + w[i];
            }
        }
    }
    //输出最终结果
    for (i = 1; i <= n; i++) {
        printf("%d", dis[i]);
    }
    getchar();getchar();
    return 0;
} 

//Bellman-Ford算法核心语句
for (k = 1; k <= n-1; k++) {
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[i]] + w[i]) {
            dis[v[i]] = dis[u[i]] + w[i];
        }
    }
}
//检测负权回路
flag = 0;
for (i = 1; i <= m; i++) {
    if (dis[v[i]] > dis[u[i]] + w[i]) {
        flag = 1;
    }
}
if (flag == 1) {
    printf("此图含有负权回路");
}

        显然，Bellman-Ford 算法的时间复杂度是 O(NM) ，这个时间复杂度貌似比Dijkstra算法还高，我们还可以对其进行优化。在实际操作中，Bellman-Ford 算法经常会在未达到n-1轮松弛前就已经计算出最短路， 之前我们已经说过，n-1 其实是最大值。因此可以添加一个一维数组用来备份数组dis。如果在新一轮的松弛中数组dis 没有发生变化， 则可以提前跳出循环， 代码如下：

#inclide <stdio.h>
int main() {
    int dis[10], bak[10], i, k, n, m, u[10], v[10], w[10], check, flag;
    int inf = 99999999;//用inf存储正无穷
    //读入n和m，n表示顶点个数，m表示边的条数
    scanf("%d %d", &n, &m);
    
    //读入边
    for (ii = 1; i <= m; i++) {
        scanf("%d %d %d", &u[i],&v[i], &w[i]);
    }
    
    //初始化dis数组，这里是1号顶点到其余各个顶点的初始路程
    for (i = 1; i <= n; i++) {
        dis[i] = inf;
    }
    dis[1] = 0;

    //Bellman-Ford算法核心语句
    for (k = 1; k <= n-1; k++) {
        //将dis数组备份至bak数组中
        for (i = 1; i <= n; i++) {
            bak[i] = dis[i];
        }
        //进行一轮松弛
        for (i = 1; i <= m; i++) {
            if (dis[v[i]] > dis[u[i]] + w[i]) {
                dis[v[i]] = dis[u[i]] + w[i];
            }
        }
        //松弛完毕后检测dis数组是否有更新
        check = 0;
        for (i = 1; i <= n; i++) {
            if (bak[i] != dis[i]) {
                check = 1;
                break;
            }
        }
        if (check == 0) {
            break;
        }
    }
    //检测负权回路
    flag = 0;
    for (i = 1; i <= m; i++) {
        if (dis[v[i]] > dis[u[i]] + w[i]) {
            flag = 1;
        }
    }

    if (flag == 1) {
        printf("此图含有负权回路");
    }
    else {
        //输出最终结果
        for (i = 1; i <= n; i++) {
            printf("%d ", dis[i]);
        }
    }
    getchar();
    getchar();
    return 0;
}

        Bellman-Ford 算法的另外一种优化在文中已经有所提示：在每实施一次松弛操作后， 就会有一些顶点已经求得其最短路， 此后这些顶点的最短路的估计值就会一直保待不变， 不再受后续松弛操作的影响， 但是每次还要判断是否需要松弛， 这里浪费了时间。这就启发我们：每次仅对最短路估计值发生变化了的顶点的所有出边执行松弛操作。详悄请看下一节：Bellman- Ford 的队列优化。
        美国应用数学家Richard Bellman （理查德·贝尔曼）千1958 年发表了该算法。此外Lester Ford, Jr在1956 年也发表了该算法。因此这个算法叫做Bellman-Ford 算法。其实EdwardF. Moore 在1957 年也发表了同样的算法， 所以这个算法也称为Bellman- Ford -Moore 算法．Edward F. Moore 很熟悉对不对？就是那个在“ 如何从迷宫中寻找出路” 问题中提出了广度优先搜索算法的那个家伙。

Bellman-Ford的队列优化

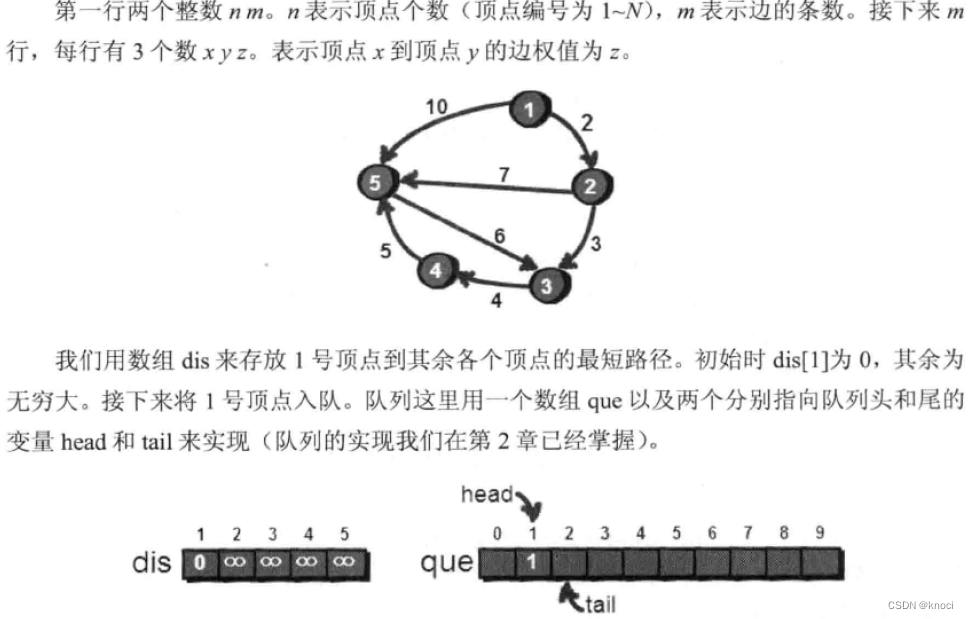
        下面是代码试下，还是用邻接表来存储图，代码如下：

#inlude <stdio.h>
int mian() {
    int n, m, i, j, k;
    //u、v和w的数组大小要根据实际情况来设置，要比m的最大值要大1
    int u[8], v[8], w[8];
    //first要比n的最大值大1，next要比m的最大值大1
    int first[6], next[8];
    int dis[6] = {0}, book[6] = {0};//book数组记录哪些顶点在队列中
    intque[101] = {0}, head = 1, tail = 1;//定义一个队列，并初始化
    int inf=99999999;
    //读入n和m
    scanf("%d %d", &n, &m);

    //初始化dis数组,这里是1号顶点到其余各个顶点的初始路程
    for (i = 1; i <= n; i++) {
        dis[i] = inf;
    }
    dis[1] = 0;

    //初始化book数组，初始化为0，刚开始都不在队列中
    for (i =1; i <= n; i++) {
        book[i] = 0;
    }

    //初始化first数组下标1~n的值为-1，表示1~n顶点暂时没有边
    for (i = 1; i <= n; i++) {
        first[i] = -1;
    }
    
    for (i =1; i <= m; i++) {
        //读入每一条边
        scanf("%d %d %d", &u[i], &v[i], &w[i]);
        //下面两句是建立邻接表的关键
        next[i] = first[u[i]];
        first[u[i]] = i;
    }

    //1号顶点入队
    que[tail++] = 1;
    book[1] = 1;//标记1号顶点已经入队
    
    while(head < tail) {
        k = first[que[head]];//当前需要处理的队列队头
        while(k != -1) {//扫描当前顶点所以边
            if (dis[v[k]] > dis[u[k]] + w[k]) {//判断是否松弛成功
                dis[v[k]] = dis[u[k]] + w[k];//更新路程
                if (book[v[k]] == 0) {//0表示不在队列，入队
                    //下面是入队操作
                    que[tail++] = v[k];
                    book[v[k]] = 1;
                }
            }
            k = next[k];
        }
        //出队
        book[que[head++]] = 0;
    }

    //输出1号顶点到其余各个顶点额最短路径
    for (i = 1; i <= n; i++) {
        printf("%d", dis[i]);
    }
    
    getchar();
    getchar();
    return 0;
}

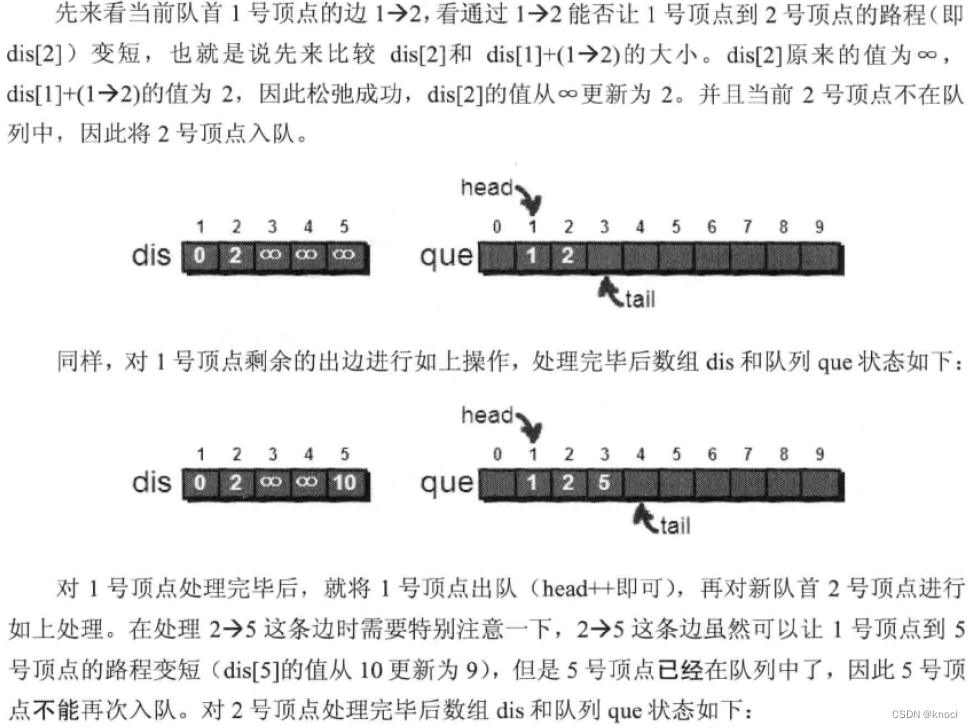
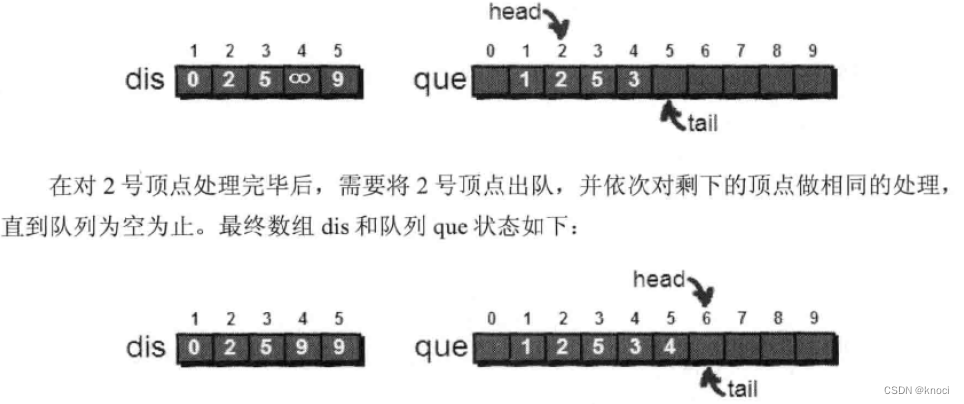
        下面来总结一下。初始时将源点加入队列。每次从队首(head) 取出一个顶点， 并对与其相邻的所有顶点进行松弛尝试， 若某个相邻的顶点松弛成功， 且这个相邻的顶点不在队列中（不在head 和tail 之间）， 则将它加入到队列中。对当前顶点处理完毕后立即出队， 并对下一个新队首进行如上操作， 直到队列为空时算法结束。这里用了一个数组book 来记录每个顶点是否处在队列中。其实也可以不要book 数组， 检查一个顶点是否在队列中， 只需要把que[head]到que[tail]依次判断一遍就可以了， 但是这样做的时间复杂度是O(N), 而使用book 数组来记录的话时间复杂度会降至0(1)。
        使用队列优化的Bellman-Ford 算法在形式上和广度优先搜索非常类似，不同的是在广度优先搜索的时候一个顶点出队后通常就不会再重新进入队列． 而这里一个顶点很可能在出队列之后再次被放入队列， 也就是当一个顶点的最短路程估计值变小后， 需要对其所有出边进行松弛， 但是如果这个顶点的最短路程估计值再次变小， 仍需要对其所有出边再次进行松弛，这样才能保证相邻顶点的最短路程估计值同步更新。需要特别说明一下的是， 使用队列优化的Bellman-Ford 算法的时间复杂度在最坏情况下也是0(NM)。通过队列优化的Bellman-Ford算法如何判断一个图是否有负环呢？如果某个点进入队列的次数超过n次， 那么这个图则肯定存在负环。
        用队列优化的Bellman-Ford 算法的关键之处在于：只有那些在前一遍松弛中改变了最短路程估计值的顶点， 才可能引起它们邻接点最短路程估计值发生改变。因此， 用一个队列来存放被成功松弛的顶点， 之后只对队列中的点进行处理， 这就降低了算法的时间复杂度。另外说一下， 西南交通大学段凡丁在1994 年发表的关千最短路径的SPFA 快速算法(SPFA,Shortest Path Faster Algorithm) ， 也是基千队列优化的Bellman-Ford 算法的。

最短路径算法对比分析

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1654103.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

学习记录：AUTOSAR R20-11的阅读记录（五）【CP（5.11-5.19）】完

学习记录：AUTOSAR R20-11的阅读记录（五）【CP（5.11-5.19）】完

接上回&#xff1a;学习记录&#xff1a;AUTOSAR R20-11的阅读记录&#xff08;四&#xff09;【CP&#xff08;5.6-5.10&#xff09;】 五、CP 11、General&#xff08;4个&#xff09; 5.11 File Name 说明 1 AUTOSAR_EXP_ LayeredSoftwareArchitecture.pdf 描述了AUTO…
阅读更多...
多模态大模型MLLM VIT CLIP BLIP

多模态大模型MLLM VIT CLIP BLIP

一、Vit模型介绍 Vit&#xff08;Vision Transformer&#xff09;即将Transformer应用于视觉领域。 Transformer输入输出都是一个序列&#xff0c;若需要应用于视觉领域&#xff0c;则需要考虑如何将一个2d图片转化为一个1d的序列&#xff0c;最直观的想法将图片中的像素点输…
阅读更多...
merge函数占用内存过大

merge函数占用内存过大

&#x1f3c6;本文收录于「Bug调优」专栏&#xff0c;主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案&#xff0c;希望能够助你一臂之力&#xff0c;帮你早日登顶实现财富自由&#x1f680;&#xff1b;同时&#xff0c;欢迎大家关注&&收藏&&…
阅读更多...
使用python将`.mat`文件转换成`.xlsx`格式的Excel文件!!

使用python将`.mat`文件转换成`.xlsx`格式的Excel文件!!

要将.mat文件转换成.xlsx格式的Excel文件 第一步&#xff1a;导入必要的库第二步&#xff1a;定义函数来转换.mat文件第三步&#xff1a;调用函数注意事项 要将.mat文件转换成.xlsx格式的Excel文件&#xff0c;并保持文件名一致&#xff0c;你可以使用scipy.io.loadmat来读取.m…
阅读更多...
历代著名画家作品赏析-东晋顾恺之

历代著名画家作品赏析-东晋顾恺之

中国历史朝代顺序为&#xff1a;夏朝、商朝、西周、东周、秦朝、西楚、西汉、新朝、玄汉、东汉、三国、曹魏、蜀汉、孙吴、西晋、东晋、十六国、南朝、刘宋、南齐、南梁、南陈、北朝、北魏、东魏、北齐、西魏、北周、隋&#xff0c;唐宋元明清&#xff0c;近代。 一、东晋著名…
阅读更多...
92、动态规划-最小路径和

92、动态规划-最小路径和

思路&#xff1a; 还是一样&#xff0c;先使用递归来接&#xff0c;无非是向右和向下&#xff0c;然后得到两种方式进行比较&#xff0c;代码如下&#xff1a; public int minPathSum(int[][] grid) {return calculate(grid, 0, 0);}private int calculate(int[][] grid, int …
阅读更多...
全栈开发之路——前端篇（5）组件间通讯和接口等知识补充

全栈开发之路——前端篇（5）组件间通讯和接口等知识补充

全栈开发一条龙——前端篇 第一篇&#xff1a;框架确定、ide设置与项目创建 第二篇&#xff1a;介绍项目文件意义、组件结构与导入以及setup的引入。 第三篇&#xff1a;setup语法&#xff0c;设置响应式数据。 第四篇&#xff1a;数据绑定、计算属性和watch监视 辅助文档&…
阅读更多...
502页 | 2024年人工智能指数报告-英文版（免费下载）

502页 | 2024年人工智能指数报告-英文版（免费下载）

【1】关注本公众号&#xff0c;转发当前文章到微信朋友圈 【2】私信发送 【2024年人工智能指数报告】 【3】获取本方案PDF下载链接&#xff0c;直接下载即可。 如需下载本方案PPT原格式&#xff0c;请加入微信扫描以下方案驿站知识星球&#xff0c;获取上万份PPT解决方案&…
阅读更多...
JavaScript快速入门系列-1（JavaScript简介）

JavaScript快速入门系列-1（JavaScript简介）

第一章：JavaScript简介 1. JavaScript简介1.1 什么是JavaScript1.2 JavaScript的历史与应用1.3 环境搭建：浏览器与Node.js2. JavaScript语言基础2.1 变量声明：let, const, var2.2 数据类型：字符串、数字、布尔值、对象、数组、null与undefined2.3 运算符：算术、比较、逻辑…
阅读更多...
html的标签

html的标签

基础标签 标签描述<h1>-<h6>定义标题&#xff0c;h1最大&#xff0c;h6最小<font>定义文本的字体&#xff0c;字体尺寸&#xff0c;字体颜色<b>定义粗体文本<i>定义斜体文本<u>定义文本下划线<center>定义文本居中<p>定义段落…
阅读更多...
Linux的虚拟机操作

Linux的虚拟机操作

一、linux系统 我们知道的系统用到的大多数是Windows系统。 Windows个人用到的有&#xff1a;win7 win10 win11 winxp 服务器用到的有&#xff1a;windows server 2003、2008、2013...........等等 linux也有系统。 centos 7 有5、6、8等等 redhat ubuntu kail 二、了…
阅读更多...
Ansible----playbook模块之templates模块、tags模块、roles模块

Ansible----playbook模块之templates模块、tags模块、roles模块

目录 引言 一、templates模块 &#xff08;一&#xff09;关键信息 &#xff08;二&#xff09;实际操作 1.定义主机组 2.设置免密登录 3.分别建立访问目录 4.定义模板文件 5.创建playbook文件 6.执行剧本 7.验证结果 二、tags模块 &#xff08;一&#xff09;创建…
阅读更多...
【自动驾驶|毫米波雷达】逻辑化讲清快时间与慢时间傅里叶变换

【自动驾驶|毫米波雷达】逻辑化讲清快时间与慢时间傅里叶变换

碎碎念&#xff1a;实习过程中发现在进行雷达知识交流时&#xff0c;大部分同事都会用英文简称代替中文的一些称呼&#xff0c;比如Chirp、FFT等等。起初我觉得是因为很多英伟达、TI芯片的开发教程都是英文的&#xff0c;所以看得多了大家都习惯这样称呼&#xff0c;后来在和指…
阅读更多...
有没有不使用技术分析工具的？众汇10年交易经验发现还真有

有没有不使用技术分析工具的？众汇10年交易经验发现还真有

不知道各位投资者有没有遇见过不使用技术分析工具的投资者&#xff0c;众汇用自己的10年外汇交易经验保证&#xff0c;别不信还真有&#xff0c;并且不在少数。 其实道理很简单&#xff0c;这些投资者不相信技术分析工具的效率!在这些投资者看来技术分析工具通常比较滞后、需要…
阅读更多...
微信小程序开发-数据事件绑定

微信小程序开发-数据事件绑定

&#x1f433;简介 数据绑定 数据绑定是一种将小程序中的数据与页面元素关联起来的技术&#xff0c;使得当数据变化时&#xff0c;页面元素能够自动更新。这通常使用特定的语法&#xff08;如双大括号 {{ }}&#xff09;来实现&#xff0c;以便在页面上展示动态数据。 事件绑…
阅读更多...
C++类和对象（基础篇）

C++类和对象（基础篇）

前言&#xff1a; 其实任何东西&#xff0c;只要你想学&#xff0c;没人能挡得住你&#xff0c;而且其实学的也很快。那么本篇开始学习类和对象&#xff08;C的&#xff0c;由于作者有Java基础&#xff0c;可能有些东西过得很快&#xff09;。 struct在C中的含义&#xff1a; …
阅读更多...
【Keil程序大小】Keil编译结果Code-RO-RW-ZI分析

【Keil程序大小】Keil编译结果Code-RO-RW-ZI分析

【Keil程序大小】Keil编译结果Code-RO-RW-ZI分析 下图为keil编译后的结果&#xff1a; 单位为Byte。Code是程序大小。RO是常量大小。RW是读写变量占用大小&#xff0c;如已初始化的静态变量和全局变量。ZI是全零变量占用大小&#xff0c;如未初始化的static修饰的静态变量、全局…
阅读更多...
ENG-2 AM，129423-53-6主要用于检测生物体系中的Na+浓度

ENG-2 AM，129423-53-6主要用于检测生物体系中的Na+浓度

引言&#xff1a;在化学研究的海洋中&#xff0c;优质的化学试剂是实验成功的关键。今天&#xff0c;我要为大家分享一款备受好评的化学试剂——ENG-2。这款试剂以其独特的性能和广泛的应用领域&#xff0c;赢得了众多科研人员的青睐。 中文名称&#xff1a;钠离子荧光探针ENG-…
阅读更多...
Linux进程——Linux进程间切换与命令行参数

Linux进程——Linux进程间切换与命令行参数

前言&#xff1a;在上一篇了解完进程状态后&#xff0c;我们简单了解了进程优先级&#xff0c;然后遗留了一点内容&#xff0c;本篇我们就来研究进程间的切换&#xff0c;来理解上篇提到的并发。如果对进程优先级还有没理解的地方可以先阅读&#xff1a; Linux进程优先级 本篇…
阅读更多...
无意的一次学习，竟让我摆脱了Android控制？

无意的一次学习，竟让我摆脱了Android控制？

由于鸿蒙的爆火&#xff0c;为了赶上时代先锋。到目前为止也研究过很长一段时间。作为一名Android的研发人员&#xff0c;免不了对其评头论足&#xff0c;指导文档如何写才算专业&#xff1f;页面如何绘制&#xff1f;页面如何跳转&#xff1f;有没有四大组件等等。 而Harmony…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023