一、定义
二叉搜索树(Binary Search Tree,BST)是一种常用的二叉树数据结构,具有以下特点:
1. **排序性质**:对于树中的每个节点,其左子树中的所有节点值都小于该节点的值,而右子树中的所有节点值都大于该节点的值。
2. **唯一性质**:二叉搜索树中不存在相同值的节点。
3. **递归性质**:二叉搜索树的左子树和右子树也分别是二叉搜索树。
这些性质使得二叉搜索树成为一种非常高效的数据结构,可以支持快速的搜索、插入和删除操作。在二叉搜索树中,搜索操作的时间复杂度为 O(log n),其中 n 是树中节点的数量(在最坏情况下可能会退化为 O(n))。
除了搜索操作,二叉搜索树还支持以下操作:
- **插入**:将新节点按照排序性质插入到树中的合适位置。
- **删除**:从树中删除指定值的节点,并保持树的排序性质不变。
- **中序遍历**:按照左根右的顺序遍历树中的所有节点,可以得到一个有序序列。
二叉搜索树的实现可以使用递归或迭代的方式,常见的实现包括普通二叉树节点的定义和相关操作,以及平衡二叉搜索树(如AVL树、红黑树)等。
二、BST的先序创建
BST的节点结构如下:
// 定义二叉树的节点结构
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} // 构造函数
};我们要建立一个 左子树 < 根节点 < 右子树的二叉树(例如下图)

我们使用前序创建上述树结构,前序创建树函数如下所示:
// 前序创建二叉树
TreeNode* createPreOrder() {
int val;
std::cin >> val;
if (val == 0) {
return nullptr;
}
TreeNode* root = new TreeNode(val);
root->left = createPreOrder();
root->right = createPreOrder();
return root;
}主函数如下:
int main() {
// 前序创建二叉树
std::cout << "Enter the elements of the tree in pre-order traversal (0 for null):\n";
TreeNode* root = createPreOrder();
// std::cout << root->val; // 输出1【测试代码】
// 前序遍历二叉树
std::cout << "Pre-order traversal of the created tree: ";
preOrderTraversal(root);
std::cout << std::endl; // 换行
// 释放内存,防止内存泄漏
delete root;
return 0;
}
运行上述代码,输入4 2 1 0 0 3 0 0 8 7 5 0 0 0 9 0 10 0 0,即可创建上述BST,该树的前序遍历结果为:4 2 1 3 8 7 5 9 10
三、BST的插入操作
例如我们要将6添加到前面的二叉树之中

// 二叉搜索树(binary search tree, BST)中添入新的元素
bool BST_InsertItem(TreeNode* T, int num) { // num表示要插入的元素
TreeNode* node = new TreeNode(num); // 定义要插入的新节点
// 第一个插入的元素为根节点
if (T == nullptr) { // 说明该二叉树为空
T = node;
}
// 二叉树不为空
while (T != nullptr) {
// 小的node插入到左子树中
if (node->val < T->val) {
// 叶子节点就插入
if (T->left == nullptr) {
T->left = node;
return true;
}
else {
// 不是叶子节点就继续,直到叶子节点
T = T->left;
}
}
// 大的node插入到右子树中
if (node->val > T->val) {
// 叶子节点就插入
if (T->right == nullptr) {
T->right = node;
return true;
}
else {
// 不是叶子节点就继续,直到叶子节点
T = T->right;
}
}
// 插入的元素与二叉树中的元素相等
if (node->val == T->val) {
return false;
}
}
}四、BST的查询操作
查询的本质类似,一个小游戏:“在100以内猜一个数,我会告诉你结果是大了还是小了。”
例如我们查询值为 6 的节点
// 二叉搜索树(binary search tree, BST)元素查询操作
TreeNode* BST_queryItem(TreeNode* T, int num) { // num表示要查询的元素
if (T == nullptr) {
std::cout << "二叉搜索树为空!" << std::endl;
}
while (T != nullptr) { // BST不为空
if (num > T->val) { // 大的节点继续右子树
T = T->right;
}
else if (num < T->val) { // 小的节点继续左子树
T = T->left;
}
else if (num == T->val) { // 相等就返回结果
return T;
}
}
// 查无此素
std::cout << "查无此素!" << std::endl;
}四、BST的改操作
改 - 修改二叉树的值
// 二叉搜索树(binary search tree, BST)元素改操作
void BST_modifyItem(TreeNode* T, int num, int modify_num) { // num表示要修改的元素,modify_num表示修改值
TreeNode* BST_node = BST_queryItem(T, num);
BST_node->val = modify_num;
}五、BST的删除操作
5.1 删除的节点为叶子节点
第一种 删除方法最简单
设立要删除的节点为current;
找到要删除的节点的父节点parent;
判断要删除的节点是父节点的左子树还是右子树;
根据节点删除方法:parent->left = nullptr;parent->right = nullptr
5.2 删除的节点只有左子树或者只有右子树
第二种 删除方法稍微有点复杂
先找到要删除的节点current;
找到要删除的节点的父节点parent;
判断current的子节点是左子树还是右子树;
判断current是父节点的左子树还是右子树;
如果 current下面是左子节点,且:
如果current是parent的左子节点-----parent.left = current.left;
如果current是parent的右子节点-----parent.right = current.left;
如果 current下面是右子节点,且:
如果current是parent的左子节点-----parent.left = current.right;
如果current是parent的右子节点-----parent.right = current.right;
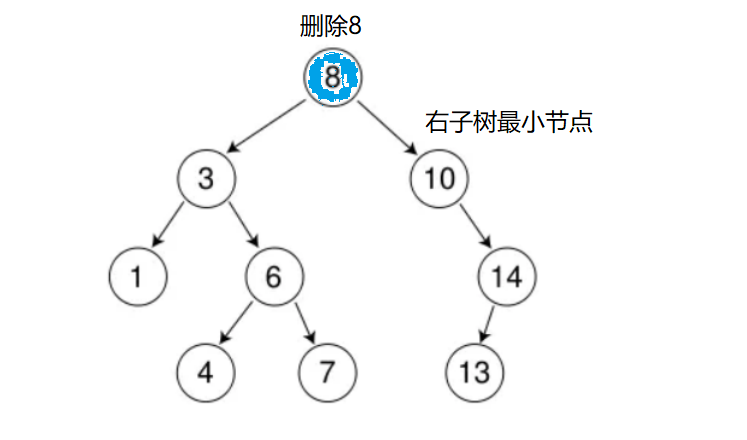
5.3 删除的节点既有左子树又有右子树
第三种 删除一个有两个子树的节点后,需要将其左子树或右子树的节点提升到删除节点的位置,以保持二叉树的结构。通常选择将右子树中的最小节点(或者左子树中的最大节点)提升到删除节点的位置,因为这样可以保持二叉搜索树的性质。
具体步骤如下:
5.4 上述三种情况的代码
// 二叉排序树元素删除操作
TreeNode* BST_deleteItem(TreeNode* root, int num) { // num表示要删除的元素
TreeNode* current = BST_queryItem(root, num); // 找到要删除的节点
TreeNode* parent = findParent(root, num); // 找到要删除的节点的父节点
if (root == nullptr) { // 说明二叉树为空,此时需要构建一颗二叉树才可进行删除操作
std::cout << "二叉树为空, 删除失败!" << std::endl;
}
// 二叉树只有一个节点时,直接删除
if (root->left == nullptr && root->right == nullptr) {
root = nullptr;
return root;
}
// 第一种情况:要删除的节点为叶子节点,此时直接删除即可
if (current->left == nullptr && current->right == nullptr) { // 条件成立,说明删除的节点为叶子节点
// 判断要删除的节点是父节点的左子节点还是右子节点
if (parent->left != nullptr && parent->left->val == num) { // 是左子节点
parent->left = nullptr;
}
else if (parent->right != nullptr && parent->right->val == num) { // 是右子节点
parent->right = nullptr;
}
}
// 第二种情况:删除有两颗子树的节点
else if (current->left != nullptr && current->right != nullptr) {
TreeNode* minRightNode = findMin(current->right); // 找到右子树中的最小节点
current->val = minRightNode->val; // 用右子树中的最小节点替换要删除的节点
current->right = BST_deleteItem(current->right, minRightNode->val); // 删除右子树中的最小节点
}
// 第三种情况:删除只有一颗子树(左子树或者右子树)的节点
else if (current->left == nullptr && current->right != nullptr) { // 删除的节点只有右子树
if (parent != nullptr) {
if (parent->left->val == num) { // 情况1:是左子节点(删除的节点相对于其父节点是左子节点)
parent->left = current->right;
}
else { // 情况2:是右子节点(删除的节点相对于其父节点是右子节点)
parent->right = current->right;
}
}
else {
root = current->right; // 情况3
}
}
else if (current->left != nullptr && current->right == nullptr) { // 删除的节点只有左子树
if (parent != nullptr) {
if (parent->left->val == num) { // 情况1:是左子节点
parent->left = current->left;
}
else { // 情况2:是右子节点
parent->right = current->left;
}
}
else {
root = current->left; // 情况3
}
}
return root;
}5.5 找寻删除节点的父节点
// 找到删除节点的父节点
TreeNode* findParent(TreeNode* root, int toDelete) { // root表示根节点,toDelete表示要删掉的元素
if (root == nullptr) return nullptr;
if (root->left != nullptr && root->left->val == toDelete) return root;
if (root->right != nullptr && root->right->val == toDelete) return root;
TreeNode* parent = findParent(root->left, toDelete);
if (parent != nullptr) return parent;
return findParent(root->right, toDelete);
}5.5 找寻最小节点
注意:BST中最左边的值最小。
// 找到以root为根的子树中最小节点
TreeNode* findMin(TreeNode* root) {
while (root->left != nullptr) {
root = root->left;
}
return root;
}六、总代码
注意,这个代码中还含有统计二叉树的性质相关部分代码。
#include <iostream>
#include <queue>
#include <cmath>
// 定义二叉树的节点结构
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} // 构造函数
};
// 前序创建二叉树
TreeNode* createPreOrder() {
int val;
std::cin >> val;
if (val == 0) {
return nullptr;
}
TreeNode* root = new TreeNode(val);
root->left = createPreOrder();
root->right = createPreOrder();
return root;
}
// 前序遍历打印二叉树
void preOrderTraversal(TreeNode* root) {
if (root) {
std::cout << root->val << " ";
preOrderTraversal(root->left);
preOrderTraversal(root->right);
}
}
// 中序遍历打印二叉树
void InOrderTraversal(TreeNode* root) {
if (root) {
InOrderTraversal(root->left);
std::cout << root->val << " ";
InOrderTraversal(root->right);
}
}
// 统计度为0的节点个数
int count_Node_0(TreeNode* T) {
if (T == nullptr) { // 二叉树为空
return 0;
}
if ((T->left == nullptr) && (T->right == nullptr)) { // 找到叶子节点
return count_Node_0(T->left) + count_Node_0(T->right) + 1;
}
else {
return count_Node_0(T->left) + count_Node_0(T->right);
}
}
// 统计度为1的节点个数
int count_Node_1(TreeNode* T) {
if (T == nullptr) {
return 0;
}
if (((T->left == nullptr)&&(T->right != nullptr)) || ((T->left != nullptr) && (T->right == nullptr))) { // 找到度为1的节点
return count_Node_1(T->left) + count_Node_1(T->right) + 1;
}
else {
return count_Node_1(T->left) + count_Node_1(T->right);
}
}
// 统计度为2的节点个数
int count_Node_2(TreeNode* T) {
if (T == nullptr) {
return 0;
}
if ((T->left != nullptr) && (T->right != nullptr)) { // 找到度为2的节点
return count_Node_2(T->left) + count_Node_2(T->right) + 1;
}
else {
return count_Node_2(T->left) + count_Node_2(T->right);
}
}
// 统计二叉树节点个数
int count_Node(TreeNode* T) {
if (T == nullptr) {
return 0;
}
return count_Node(T->left) + count_Node(T->right) + 1; // 总节点个数=左子树节点数+右子树节点数+根结点数(1)
}
// 计算二叉树的深度
int Depth(TreeNode* T) {
if (T == nullptr) { // 二叉树为空,则深度为0
return 0;
}
else {
int m = Depth(T->left);
int n = Depth(T->right);
if (m > n) {
return m + 1;
}
else {
return n + 1;
}
}
}
// 层序遍历
void level_order_tras(TreeNode* T) {
if (T == nullptr) { // 代码若改为if (T = nullptr) 则会引出下面两个错误
return;
}
// 创建队列,用于存放待访问的节点
std::queue<TreeNode*> q;
// 将根节点入队
q.push(T);
// std::cout << T->val; // 报错【测试代码】
// std::cout << q.front()->val; // 报错【测试代码】
//开始层序遍历
while (!q.empty()) {
// 确定当前层节点个数
int levelSize = q.size();
//遍历当前层的所有节点
for (int i = 0; i < levelSize; ++i) {
// 取出队首节点
TreeNode* node = q.front();
q.pop();
// 输出节点值
std::cout << node->val << " ";
// 将当前节点的左右子节点入队
if (node->left != nullptr) {
q.push(node->left);
}
if (node->right != nullptr) {
q.push(node->right);
}
}
}
}
// 层序遍历(每层输出)
void level_print(TreeNode* T) {
if (T == nullptr) {
return;
}
// 创建队列,用于存放待访问的节点
std::queue<TreeNode*> q;
// 将根节点入队
q.push(T);
int j = 1; // j表示层数
//开始层序遍历
while (!q.empty()) {
std::cout << "第" << j << "层的数据为:";
// 确定当前层节点个数
int levelSize = q.size();
//遍历当前层的所有节点
for (int i = 0; i < levelSize; i++) {
// 取出队首节点
TreeNode* node = q.front();
q.pop();
std::cout << node->val << " ";
// 将当前节点的左右子节点入队
if (node->left != nullptr) {
q.push(node->left);
}
if (node->right != nullptr) {
q.push(node->right);
}
}
j++;
std::cout << std::endl; // 换行
}
}
/*
// 判断一个二叉树是否为完全二叉树
void Complete_binary_tree(TreeNode* T) { // 【错误代码】
// 思路:具有n个节点的完全二叉树的深度为{log2n}+1(2为底数,{}表示向下取整 )
if (T == nullptr) {
std::cout << "该二叉树是一颗空二叉树!" << std::endl;
}
int h = Depth(T); // 获取二叉树的深度,即层数
int node = count_Node(T); // 获取二叉树的节点总数
// 使用换底公式定义以2为底数的对数函数
double log_2_node = log(node) / log(2);// 计算以e为底的对数,即ln(x)
std::cout << "log_2_node:" << log_2_node;
if (h == (floor(log_2_node) + 1)) {
std::cout << "这颗二叉树是一颗完全二叉树!" << std::endl;
}
std::cout << "这颗二叉树不是一颗完全二叉树!" << std::endl;
}
*/
// 判断是否为完全二叉树
/*
基本思路:使用队列按层次遍历二叉树,遍历过程中将二叉树的所有结点依次入队。
当出队遇见一个NULL结点时,若遍历其后结点都为NULL则为完全二叉树,否则不是完全二叉树。
因为层次遍历完全二叉树时,当遍历到空结点时前面所有非空结点已经被遍历完了,若空结点之后还有非空结点则不是完全二叉树。
*/
bool Complete_binary_tree(TreeNode* T) {
if (T == nullptr) {
std::cout << "该二叉树是一颗空二叉树!" << std::endl;
}
// 创建队列,用于存放待访问的节点
std::queue<TreeNode*> q;
// 将根节点入队
q.push(T);
bool encounteredNull = false; // 是否遇到过空节点
//开始层序遍历
while (!q.empty()) { // 队列不为空
// 取出队首节点
TreeNode* current = q.front();
q.pop();
if (current == nullptr) {
encounteredNull = true;
continue;
}
if (encounteredNull && current != nullptr) {
// 遇到空节点后面还有非空节点,则说明不是完全二叉树
return false;
}
q.push(current->left);
q.push(current->right);
}
return true;
}
// 判断一个二叉树是否为满二叉树
void Full_binary_tree(TreeNode* T) {
if (T == nullptr) {
std::cout << "该二叉树是一颗空二叉树!" << std::endl;
}
int h = Depth(T); // 获取二叉树的深度,即层数
int node = count_Node(T); // 获取二叉树的节点总数
if (node == (2 ^ h) - 1) { // 说明二叉树为满二叉树
std::cout << "该二叉树是一颗满二叉树!" << std::endl;
std::cout << "深度为:" << h << "," << "节点总数为:" << node << std::endl;
}
else {
std::cout << "这颗二叉树不是满二叉树!" << std::endl;
std::cout << "深度为:" << h << "," << "节点总数为:" << node << std::endl;
}
}
// 二叉搜索树(binary search tree, BST)中添入新的元素
bool BST_InsertItem(TreeNode* T, int num) { // num表示要插入的元素
TreeNode* node = new TreeNode(num); // 定义要插入的新节点
// 第一个插入的元素为根节点
if (T == nullptr) { // 说明该二叉树为空
T = node;
}
// 二叉树不为空
while (T != nullptr) {
// 小的node插入到左子树中
if (node->val < T->val) {
// 叶子节点就插入
if (T->left == nullptr) {
T->left = node;
return true;
}
else {
// 不是叶子节点就继续,直到叶子节点
T = T->left;
}
}
// 大的node插入到右子树中
if (node->val > T->val) {
// 叶子节点就插入
if (T->right == nullptr) {
T->right = node;
return true;
}
else {
// 不是叶子节点就继续,直到叶子节点
T = T->right;
}
}
// 插入的元素与二叉树中的元素相等
if (node->val == T->val) {
return false;
}
}
}
// 二叉搜索树(binary search tree, BST)元素查询操作
TreeNode* BST_queryItem(TreeNode* T, int num) { // num表示要查询的元素
if (T == nullptr) {
std::cout << "二叉搜索树为空!" << std::endl;
}
while (T != nullptr) { // BST不为空
if (num > T->val) { // 大的节点继续右子树
T = T->right;
}
else if (num < T->val) { // 小的节点继续左子树
T = T->left;
}
else if (num == T->val) { // 相等就返回结果
return T;
}
}
// 查无此素
std::cout << "查无此素!" << std::endl;
}
// 二叉搜索树(binary search tree, BST)元素改操作
void BST_modifyItem(TreeNode* T, int num, int modify_num) { // num表示要修改的元素,modify_num表示修改值
TreeNode* BST_node = BST_queryItem(T, num);
BST_node->val = modify_num;
}
// 找到删除节点的父节点
TreeNode* findParent(TreeNode* root, int toDelete) { // root表示根节点,toDelete表示要删掉的元素
if (root == nullptr) return nullptr;
if (root->left != nullptr && root->left->val == toDelete) return root;
if (root->right != nullptr && root->right->val == toDelete) return root;
TreeNode* parent = findParent(root->left, toDelete);
if (parent != nullptr) return parent;
return findParent(root->right, toDelete);
}
// 找到以root为根的子树中最小节点
TreeNode* findMin(TreeNode* root) {
while (root->left != nullptr) {
root = root->left;
}
return root;
}
// 二叉排序树元素删除操作
TreeNode* BST_deleteItem(TreeNode* root, int num) { // num表示要删除的元素
TreeNode* current = BST_queryItem(root, num); // 找到要删除的节点
TreeNode* parent = findParent(root, num); // 找到要删除的节点的父节点
if (root == nullptr) { // 说明二叉树为空,此时需要构建一颗二叉树才可进行删除操作
std::cout << "二叉树为空, 删除失败!" << std::endl;
}
// 二叉树只有一个节点时,直接删除
if (root->left == nullptr && root->right == nullptr) {
root = nullptr;
return root;
}
// 第一种情况:要删除的节点为叶子节点,此时直接删除即可
if (current->left == nullptr && current->right == nullptr) { // 条件成立,说明删除的节点为叶子节点
// 判断要删除的节点是父节点的左子节点还是右子节点
if (parent->left != nullptr && parent->left->val == num) { // 是左子节点
parent->left = nullptr;
}
else if (parent->right != nullptr && parent->right->val == num) { // 是右子节点
parent->right = nullptr;
}
}
// 第二种情况:删除有两颗子树的节点
else if (current->left != nullptr && current->right != nullptr) {
TreeNode* minRightNode = findMin(current->right); // 找到右子树中的最小节点
current->val = minRightNode->val; // 用右子树中的最小节点替换要删除的节点
current->right = BST_deleteItem(current->right, minRightNode->val); // 删除右子树中的最小节点
}
// 第三种情况:删除只有一颗子树(左子树或者右子树)的节点
else if (current->left == nullptr && current->right != nullptr) { // 删除的节点只有右子树
if (parent != nullptr) {
if (parent->left->val == num) { // 情况1:是左子节点(删除的节点相对于其父节点是左子节点)
parent->left = current->right;
}
else { // 情况2:是右子节点(删除的节点相对于其父节点是右子节点)
parent->right = current->right;
}
}
else {
root = current->right; // 情况3
}
}
else if (current->left != nullptr && current->right == nullptr) { // 删除的节点只有左子树
if (parent != nullptr) {
if (parent->left->val == num) { // 情况1:是左子节点
parent->left = current->left;
}
else { // 情况2:是右子节点
parent->right = current->left;
}
}
else {
root = current->left; // 情况3
}
}
return root;
}
// 平衡二叉树
int main() {
// 前序创建二叉树
std::cout << "Enter the elements of the tree in pre-order traversal (0 for null):\n";
TreeNode* root = createPreOrder();
// std::cout << root->val; // 输出1【测试代码】
前序遍历二叉树
//std::cout << "Pre-order traversal of the created tree: ";
//preOrderTraversal(root);
//std::cout << std::endl; // 换行
二叉搜索树中添入新的元素6
//if (BST_InsertItem(root, 6)) {
// std::cout << "二叉搜索树插入元素成功!" << std::endl;
//}
//else {
// std::cout << "二叉搜索树插入元素失败!" << std::endl;
//}
前序遍历二叉树
//std::cout << "Pre-order traversal of the created tree: ";
//preOrderTraversal(root);
//std::cout << std::endl; // 换行
二叉搜索树查询操作
//TreeNode * query_T = BST_queryItem(root, 6);
//std::cout << "查询的节点情况如下:" << std::endl;
//std::cout << "节点值:" << query_T->val << std::endl;
二叉搜索树改操作
//std::cout << "二叉树修改操作如下,将10修改为11:" << std::endl;
//BST_modifyItem(root, 10, 11);
std::cout << "删除操作前二叉树的前序遍历:" << std::endl;
// 前序遍历二叉树
std::cout << "Pre-order traversal of the created tree: ";
preOrderTraversal(root);
std::cout << std::endl; // 换行
// 二叉树的删除操作
BST_deleteItem(root, 2);
std::cout << "删除操作后二叉树的前序遍历:" << std::endl;
// 前序遍历二叉树
std::cout << "Pre-order traversal of the created tree: ";
preOrderTraversal(root);
std::cout << std::endl; // 换行
中序遍历二叉树
//std::cout << "In-order traversal of the created tree: ";
//InOrderTraversal(root);
//std::cout << std::endl; // 换行
//
统计度为0的节点个数
//int Node0_n = count_Node_0(root);
//std::cout << "度为0的节点个数为:" << Node0_n << std::endl;
//
统计度为1的节点个数
//int Node1_n = count_Node_1(root);
//std::cout << "度为1的节点个数为:" << Node1_n << std::endl;
统计度为2的节点个数
//int Node2_n = count_Node_2(root);
//std::cout << "度为2的节点个数为:" << Node2_n << std::endl;
统计二叉树的节点个数
//int Node = count_Node(root);
//std::cout << "节点个数为:" << Node << std::endl;
//
计算二叉树的深度
//int depth = Depth(root);
//std::cout << "二叉树的深度为:" << depth << std::endl;
二叉树的层序遍历(一次性输出)
//std::cout << "二叉树的层序遍历结果如下:" << std::endl;
//level_order_tras(root);
//std::cout << std::endl;
二叉树的层序打印(每层输出)
//std::cout << "二叉树的每层输出结果如下:" << std::endl;
//level_print(root);
//std::cout << std::endl; // 换行
判断二叉树是否为满二叉树
//Full_binary_tree(root);
判断二叉树是否为完全二叉树
//if (Complete_binary_tree(root)) {
// std::cout << "这颗二叉树是一颗完全二叉树!" << std::endl;
//}
//else {
// std::cout << "这颗二叉树不是一颗完全二叉树!" << std::endl;
//}
// 释放内存,防止内存泄漏
delete root;
return 0;
}