阅读目录
- 1. 题目
- 2. 解题思路一
- 3. 代码实现一
- 4. 解题思路二
- 5. 代码实现二
1. 题目
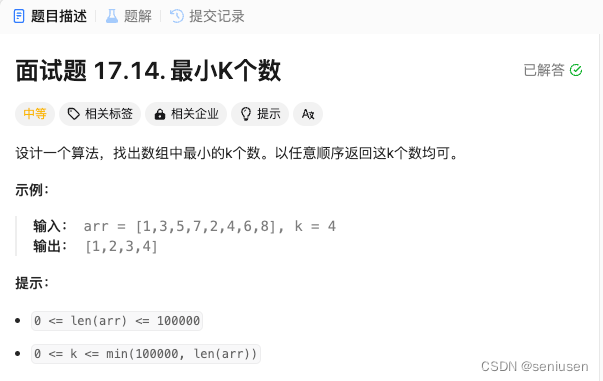
2. 解题思路一
第一种方法就是利用快速排序,第一次排序后,数组被划分为了左右两个区间 [ 0 , i ] , [ i + 1 , a r r . s i z e ( ) − 1 ] [0, i], [i+1, arr.size()-1] [0,i],[i+1,arr.size()−1]。如果此时,恰好有 i = k − 1 i=k-1 i=k−1,那么左边的区间就正好是我们要找的最小的 K K K 个数。如果此时有 i < k − 1 i<k-1 i<k−1,那么我们要找的分区点就落在右边区间,我们去右边区间继续递归寻找。而如果此时有 i > k − 1 i>k-1 i>k−1,那么我们要找的分区点就落在左边区间,我们去左边区间继续递归寻找。
3. 代码实现一
class Solution {
public:
void quickSort(vector<int>& arr, int left, int right, int k) {
if (left <= right) {
int pivot = arr[right];
int i = left;
for (int j = left; j <= right; ++j){
if (arr[j] <= pivot) {
int temp = arr[i];
arr[i++] = arr[j];
arr[j] = temp;
}
}
--i; // 此时,i左边的元素都小于等于pivot
if (i == k - 1) {
return;
} else if (i < k - 1) {
quickSort(arr, i+1, right, k);
} else {
quickSort(arr, left, i-1, k);
}
}
}
vector<int> smallestK(vector<int>& arr, int k) {
vector<int> ret;
if (arr.empty() || k == 0) {
return ret;
}
if (k == arr.size()) {
return arr;
}
quickSort(arr, 0, arr.size()-1, k);
ret.assign(arr.begin(), arr.begin()+k);
return ret;
}
};
4. 解题思路二
第二种方法就是利用堆,我们对数组前 K K K 个元素建一个大顶堆,树顶的元素是最大的,然后,从第 K + 1 K+1 K+1 个元素开始遍历,如果其小于堆顶元素,那么就拿它替换掉堆顶元素,并将其插入到堆中的合适位置,最后,整个数组都访问后留在堆中的 K K K 个元素即是我们所求。
5. 代码实现二
class Solution {
public:
void heapify(vector<int>& arr, int i, int n) {
int j = i;
while (j < n) {
if (2*i+1 < n && arr[j] < arr[2*i+1]) {
j = 2 * i + 1;
}
if (2*i+2 < n && arr[j] < arr[2*i+2]) {
j = 2 * i + 2;
}
if (i != j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i = j;
} else {
break;
}
}
}
vector<int> smallestK(vector<int>& arr, int k) {
vector<int> ret;
if (arr.empty() || k == 0) {
return ret;
}
if (arr.size() == k) {
return arr;
}
// 第一步,对数组中的前K个元素建立大顶堆
// (k-1)/2的左子结点是k,右子节点是k+1,超出k-1(堆的最后一个元素)了,所以(k-2)/2是第一个叶子结点
// 我们从叶子结点上面的节点开始向下堆化来建堆
for (int i = (k-2)/2; i >= 0; --i) {
heapify(arr, i, k);
}
// 遍历数组k之后的元素,插入堆中
for (int i = k; i < arr.size(); ++i) {
if (arr[i] < arr[0]) {
arr[0] = arr[i];
heapify(arr, 0, k);
}
}
ret.assign(arr.begin(), arr.begin()+k);
return ret;
}
};