2385. 感染二叉树需要的总时间
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
节点此前还没有感染。
节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
示例 1:
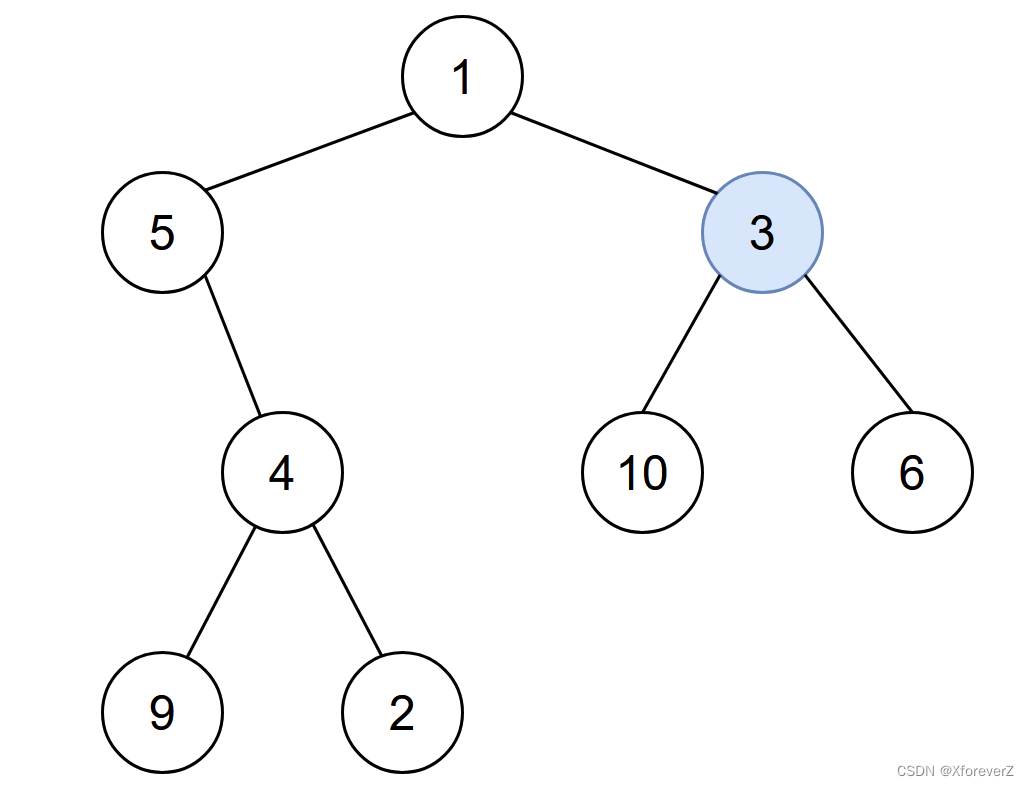
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。
示例 2:

输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
树中节点的数目在范围 [1, 105] 内
1 <= Node.val <= 105
每个节点的值 互不相同
树中必定存在值为 start 的节点
哈希映射+DFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
int amountOfTime(TreeNode* root, int start) {
unordered_map<int, vector<int>> graph;
buildGraph(root, graph, NULL);
queue<int> q;
unordered_set<int> visited;
q.push(start);
visited.insert(start);
int minutes = 0;
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; ++i) {
int node = q.front();
q.pop();
for (int neighbor : graph[node]) {
if (visited.count(neighbor) == 0) {
q.push(neighbor);
visited.insert(neighbor);
}
}
}
if (!q.empty()) {
++minutes;
}
}
return minutes;
}
private:
void buildGraph(TreeNode* node, unordered_map<int, vector<int>>& graph,
TreeNode* parent) {
if (node == NULL)
return;
if (parent != NULL) {
graph[node->val].push_back(parent->val);
graph[parent->val].push_back(node->val);
}
buildGraph(node->left, graph, node);
buildGraph(node->right, graph, node);
}
};
2739. 总行驶距离
卡车有两个油箱。给你两个整数,mainTank 表示主油箱中的燃料(以升为单位),additionalTank 表示副油箱中的燃料(以升为单位)。
该卡车每耗费 1 升燃料都可以行驶 10 km。每当主油箱使用了 5 升燃料时,如果副油箱至少有 1 升燃料,则会将 1 升燃料从副油箱转移到主油箱。
返回卡车可以行驶的最大距离。
注意:从副油箱向主油箱注入燃料不是连续行为。这一事件会在每消耗 5 升燃料时突然且立即发生。
示例 1:
输入:mainTank = 5, additionalTank = 10
输出:60
解释:
在用掉 5 升燃料后,主油箱中燃料还剩下 (5 - 5 + 1) = 1 升,行驶距离为 50km 。
在用掉剩下的 1 升燃料后,没有新的燃料注入到主油箱中,主油箱变为空。
总行驶距离为 60km 。
示例 2:
输入:mainTank = 1, additionalTank = 2
输出:10
解释:
在用掉 1 升燃料后,主油箱变为空。
总行驶距离为 10km 。
提示:
1 <= mainTank, additionalTank <= 100
简单模拟:
class Solution {
public:
int distanceTraveled(int mainTank, int additionalTank) {
int ans = 0;
while (mainTank >= 5) {
mainTank -= 5;
ans += 50;
if (additionalTank) {
additionalTank--;
mainTank++;
}
}
return ans + mainTank * 10;
}
};
1146. 快照数组
实现支持下列接口的「快照数组」- SnapshotArray:
SnapshotArray(int length) - 初始化一个与指定长度相等的 类数组 的数据结构。初始时,每个元素都等于 0。
void set(index, val) - 会将指定索引 index 处的元素设置为 val。
int snap() - 获取该数组的快照,并返回快照的编号 snap_id(快照号是调用 snap() 的总次数减去 1)。
int get(index, snap_id) - 根据指定的 snap_id 选择快照,并返回该快照指定索引 index 的值。
示例:
输入:[“SnapshotArray”,“set”,“snap”,“set”,“get”]
[[3],[0,5],[],[0,6],[0,0]]
输出:[null,null,0,null,5]
解释:
SnapshotArray snapshotArr = new SnapshotArray(3); // 初始化一个长度为 3 的快照数组
snapshotArr.set(0,5); // 令 array[0] = 5
snapshotArr.snap(); // 获取快照,返回 snap_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0); // 获取 snap_id = 0 的快照中 array[0] 的值,返回 5
提示:
1 <= length <= 50000
题目最多进行50000 次set,snap,和 get的调用 。
0 <= index < length
0 <= snap_id < 我们调用 snap() 的总次数
0 <= val <= 10^9
二分查找:
class SnapshotArray {
public:
SnapshotArray(int length) : snap_cnt(0), data(length) {}
void set(int index, int val) { data[index].emplace_back(snap_cnt, val); }
int snap() { return snap_cnt++; }
int get(int index, int snap_id) {
auto x = upper_bound(data[index].begin(), data[index].end(),
pair{snap_id + 1, -1});
return x == data[index].begin() ? 0 : prev(x)->second;
}
private:
int snap_cnt;
vector<vector<pair<int, int>>> data;
};
2639. 查询网格图中每一列的宽度
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。矩阵中某一列的宽度是这一列数字的最大 字符串长度 。
比方说,如果 grid = [[-10], [3], [12]] ,那么唯一一列的宽度是 3 ,因为 -10 的字符串长度为 3 。
请你返回一个大小为 n 的整数数组 ans ,其中 ans[i] 是第 i 列的宽度。
一个有 len 个数位的整数 x ,如果是非负数,那么 字符串长度 为 len ,否则为 len + 1 。
示例 1:
输入:grid = [[1],[22],[333]]
输出:[3]
解释:第 0 列中,333 字符串长度为 3 。
示例 2:
输入:grid = [[-15,1,3],[15,7,12],[5,6,-2]]
输出:[3,1,2]
解释:
第 0 列中,只有 -15 字符串长度为 3 。
第 1 列中,所有整数的字符串长度都是 1 。
第 2 列中,12 和 -2 的字符串长度都为 2 。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 100
-1e9 <= grid[r][c] <= 1e9
模拟即可:
class Solution {
public:
vector<int> findColumnWidth(vector<vector<int>>& grid) {
int n = grid[0].size();
vector<int> ans(n);
for (int j = 0; j < n; j++) {
for (auto& row : grid) {
ans[j] = max(ans[j], (int)to_string(row[j]).length());
}
}
return ans;
}
};
1017. 负二进制转换
给你一个整数 n ,以二进制字符串的形式返回该整数的 负二进制(base -2)表示。
注意,除非字符串就是 “0”,否则返回的字符串中不能含有前导零。
示例 1:
输入:n = 2
输出:“110”
解释:(-2)2 + (-2)1 = 2
示例 2:
输入:n = 3
输出:“111”
解释:(-2)2 + (-2)1 + (-2)0 = 3
示例 3:
输入:n = 4
输出:“100”
解释:(-2)2 = 4
提示:
0 <= n <= 1e9
模拟:
class Solution {
public:
string baseNeg2(int n) {
if (n == 0) {
return "0";
}
string ans;
while (n != 0) {
int remainder = n % (-2);
n /= -2;
if (remainder < 0) {
remainder += 2;
n += 1;
}
ans = to_string(remainder) + ans;
}
return ans;
}
};
1329. 将矩阵按对角线排序
矩阵对角线 是一条从矩阵最上面行或者最左侧列中的某个元素开始的对角线,沿右下方向一直到矩阵末尾的元素。例如,矩阵 mat 有 6 行 3 列,从 mat[2][0] 开始的 矩阵对角线 将会经过 mat[2][0]、mat[3][1] 和 mat[4][2] 。
给你一个 m * n 的整数矩阵 mat ,请你将同一条 矩阵对角线 上的元素按升序排序后,返回排好序的矩阵。
示例 1:
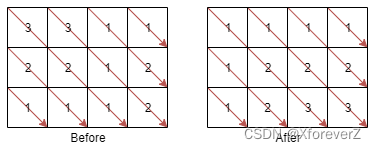
输入:mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出:[[1,1,1,1],[1,2,2,2],[1,2,3,3]]
示例 2:
输入:mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
输出:[[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
提示:
m == mat.length
n == mat[i].length
1 <= m, n <= 100
1 <= mat[i][j] <= 100
对角线排序,哈希:
class Solution {
public:
vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
unordered_map<int, priority_queue<int, vector<int>, greater<int>>> m;
int row = mat.size(), col = mat[0].size();
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
m[i - j].push(mat[i][j]);
}
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
mat[i][j] = m[i - j].top();
m[i - j].pop();
}
}
return mat;
}
};
2798. 满足目标工作时长的员工数目
公司里共有 n 名员工,按从 0 到 n - 1 编号。每个员工 i 已经在公司工作了 hours[i] 小时。
公司要求每位员工工作 至少 target 小时。
给你一个下标从 0 开始、长度为 n 的非负整数数组 hours 和一个非负整数 target 。
请你用整数表示并返回工作至少 target 小时的员工数。
示例 1:
输入:hours = [0,1,2,3,4], target = 2
输出:3
解释:公司要求每位员工工作至少 2 小时。
- 员工 0 工作 0 小时,不满足要求。
- 员工 1 工作 1 小时,不满足要求。
- 员工 2 工作 2 小时,满足要求。
- 员工 3 工作 3 小时,满足要求。
- 员工 4 工作 4 小时,满足要求。
共有 3 位满足要求的员工。
示例 2:
输入:hours = [5,1,4,2,2], target = 6
输出:0
解释:公司要求每位员工工作至少 6 小时。
共有 0 位满足要求的员工。
提示:
1 <= n == hours.length <= 50
0 <= hours[i], target <= 1e5
简单模拟:
class Solution {
public:
int numberOfEmployeesWhoMetTarget(vector<int>& hours, int target) {
int cnt = 0;
for (int i = 0; i < hours.size(); i++) {
if (hours[i] >= target) {
cnt++;
}
}
return cnt;
}
};
2462. 雇佣 K 位工人的总代价
给你一个下标从 0 开始的整数数组 costs ,其中 costs[i] 是雇佣第 i 位工人的代价。
同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人:
总共进行 k 轮雇佣,且每一轮恰好雇佣一位工人。
在每一轮雇佣中,从最前面 candidates 和最后面 candidates 人中选出代价最小的一位工人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。
比方说,costs = [3,2,7,7,1,2] 且 candidates = 2 ,第一轮雇佣中,我们选择第 4 位工人,因为他的代价最小 [3,2,7,7,1,2] 。
第二轮雇佣,我们选择第 1 位工人,因为他们的代价与第 4 位工人一样都是最小代价,而且下标更小,[3,2,7,7,2] 。注意每一轮雇佣后,剩余工人的下标可能会发生变化。
如果剩余员工数目不足 candidates 人,那么下一轮雇佣他们中代价最小的一人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。
一位工人只能被选择一次。
返回雇佣恰好 k 位工人的总代价。
示例 1:
输入:costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
输出:11
解释:我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣,我们从 [17,12,10,2,7,2,11,20,8] 中选择。最小代价是 2 ,有两位工人,我们选择下标更小的一位工人,即第 3 位工人。总代价是 0 + 2 = 2 。
- 第二轮雇佣,我们从 [17,12,10,7,2,11,20,8] 中选择。最小代价是 2 ,下标为 4 ,总代价是 2 + 2 = 4 。
- 第三轮雇佣,我们从 [17,12,10,7,11,20,8] 中选择,最小代价是 7 ,下标为 3 ,总代价是 4 + 7 = 11 。注意下标为 3 的工人同时在最前面和最后面 4 位工人中。
总雇佣代价是 11 。
示例 2:
输入:costs = [1,2,4,1], k = 3, candidates = 3
输出:4
解释:我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣,我们从 [1,2,4,1] 中选择。最小代价为 1 ,有两位工人,我们选择下标更小的一位工人,即第 0 位工人,总代价是 0 + 1 = 1 。注意,下标为 1 和 2 的工人同时在最前面和最后面 3 位工人中。
- 第二轮雇佣,我们从 [2,4,1] 中选择。最小代价为 1 ,下标为 2 ,总代价是 1 + 1 = 2 。
- 第三轮雇佣,少于 3 位工人,我们从剩余工人 [2,4] 中选择。最小代价是 2 ,下标为 0 。总代价为 2 + 2 = 4 。
总雇佣代价是 4 。
提示:
1 <= costs.length <= 1e5
1 <= costs[i] <= 1e5
1 <= k, candidates <= costs.length
最小堆模拟(菜鸡不会,抄了灵神):
class Solution {
public:
long long totalCost(vector<int>& costs, int k, int candidates) {
int n = costs.size();
if (candidates * 2 + k > n) {
ranges::nth_element(costs, costs.begin() + k);
return accumulate(costs.begin(), costs.begin() + k, 0LL);
}
priority_queue<int, vector<int>, greater<>> pre, suf;
for (int i = 0; i < candidates; i++) {
pre.push(costs[i]);
suf.push(costs[n - 1 - i]);
}
long long ans = 0;
int i = candidates, j = n - 1 - candidates;
while (k--) {
if (pre.top() <= suf.top()) {
ans += pre.top();
pre.pop();
pre.push(costs[i++]);
} else {
ans += suf.top();
suf.pop();
suf.push(costs[j--]);
}
}
return ans;
}
};
857. 雇佣 K 名工人的最低成本(Hard)
有 n 名工人。 给定两个数组 quality 和 wage ,其中,quality[i] 表示第 i 名工人的工作质量,其最低期望工资为 wage[i] 。
现在我们想雇佣 k 名工人组成一个工资组。在雇佣 一组 k 名工人时,我们必须按照下述规则向他们支付工资:
对工资组中的每名工人,应当按其工作质量与同组其他工人的工作质量的比例来支付工资。
工资组中的每名工人至少应当得到他们的最低期望工资。
给定整数 k ,返回 组成满足上述条件的付费群体所需的最小金额 。在实际答案的 10-5 以内的答案将被接受。。
示例 1:
输入: quality = [10,20,5], wage = [70,50,30], k = 2
输出: 105.00000
解释: 我们向 0 号工人支付 70,向 2 号工人支付 35。
示例 2:
输入: quality = [3,1,10,10,1], wage = [4,8,2,2,7], k = 3
输出: 30.66667
解释: 我们向 0 号工人支付 4,向 2 号和 3 号分别支付 13.33333。
提示:
n == quality.length == wage.length
1 <= k <= n <= 1e4
1 <= quality[i], wage[i] <= 1e4
贪心+优先队列(思路居然和ylb大佬一样):
class Solution {
public:
double mincostToHireWorkers(vector<int>& quality, vector<int>& wage,
int K) {
int n = quality.size();
vector<pair<double, int>> workers(n);
for (int i = 0; i < n; ++i) {
workers[i] = {double(wage[i]) / quality[i], quality[i]};
}
sort(workers.begin(), workers.end());
double res = 1e9, qsum = 0;
priority_queue<int> pq;
for (auto worker : workers) {
double ratio = worker.first;
int q = worker.second;
qsum += q;
pq.push(q);
if (pq.size() > K) {
qsum -= pq.top();
pq.pop();
}
if (pq.size() == K) {
res = min(res, ratio * qsum);
}
}
return res;
}
};
1491. 去掉最低工资和最高工资后的工资平均值
给你一个整数数组 salary ,数组里每个数都是 唯一 的,其中 salary[i] 是第 i 个员工的工资。
请你返回去掉最低工资和最高工资以后,剩下员工工资的平均值。
示例 1:
输入:salary = [4000,3000,1000,2000]
输出:2500.00000
解释:最低工资和最高工资分别是 1000 和 4000 。
去掉最低工资和最高工资以后的平均工资是 (2000+3000)/2= 2500
示例 2:
输入:salary = [1000,2000,3000]
输出:2000.00000
解释:最低工资和最高工资分别是 1000 和 3000 。
去掉最低工资和最高工资以后的平均工资是 (2000)/1= 2000
示例 3:
输入:salary = [6000,5000,4000,3000,2000,1000]
输出:3500.00000
示例 4:
输入:salary = [8000,9000,2000,3000,6000,1000]
输出:4750.00000
提示:
3 <= salary.length <= 100
10^3 <= salary[i] <= 10^6
salary[i] 是唯一的。
与真实值误差在 10^-5 以内的结果都将视为正确答案。
简单模拟:
class Solution {
public:
double average(vector<int>& salary) {
sort(salary.begin(), salary.end());
double sum = 0;
for (int i = 1; i < salary.size() - 1; i++) {
sum += salary[i];
}
return sum/(salary.size() - 2);
}
};
1235. 规划兼职工作(Hard)
你打算利用空闲时间来做兼职工作赚些零花钱。
这里有 n 份兼职工作,每份工作预计从 startTime[i] 开始到 endTime[i] 结束,报酬为 profit[i]。
给你一份兼职工作表,包含开始时间 startTime,结束时间 endTime 和预计报酬 profit 三个数组,请你计算并返回可以获得的最大报酬。
注意,时间上出现重叠的 2 份工作不能同时进行。
如果你选择的工作在时间 X 结束,那么你可以立刻进行在时间 X 开始的下一份工作。
示例 1:
输入:startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出:120
解释:
我们选出第 1 份和第 4 份工作,
时间范围是 [1-3]+[3-6],共获得报酬 120 = 50 + 70。
示例 2:
输入:startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出:150
解释:
我们选择第 1,4,5 份工作。
共获得报酬 150 = 20 + 70 + 60。
示例 3:
输入:startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出:6
提示:
1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4
DP+二分(灵神题解):
class Solution {
public:
int jobScheduling(vector<int> &startTime, vector<int> &endTime, vector<int> &profit) {
int n = startTime.size();
vector<array<int, 3>> jobs(n);
for (int i = 0; i < n; i++) {
jobs[i] = {endTime[i], startTime[i], profit[i]};
}
ranges::sort(jobs, [](auto &a, auto &b) { return a[0] < b[0]; }); // 按照结束时间排序
vector<int> f(n + 1);
for (int i = 0; i < n; i++) {
int j = upper_bound(jobs.begin(), jobs.begin() + i, array<int, 3>{jobs[i][1], INT_MAX}) - jobs.begin();
// 状态转移中,为什么是 j 不是 j+1:上面算的是 > 开始时间,-1 后得到 <= 开始时间,但由于还要 +1,抵消了
f[i + 1] = max(f[i], f[j] + jobs[i][2]);
}
return f[n];
}
};
题解:动态规划 + 二分查找优化
1652. 拆炸弹
你有一个炸弹需要拆除,时间紧迫!你的情报员会给你一个长度为 n 的 循环 数组 code 以及一个密钥 k 。
为了获得正确的密码,你需要替换掉每一个数字。所有数字会 同时 被替换。
如果 k > 0 ,将第 i 个数字用 接下来 k 个数字之和替换。
如果 k < 0 ,将第 i 个数字用 之前 k 个数字之和替换。
如果 k == 0 ,将第 i 个数字用 0 替换。
由于 code 是循环的, code[n-1] 下一个元素是 code[0] ,且 code[0] 前一个元素是 code[n-1] 。
给你 循环 数组 code 和整数密钥 k ,请你返回解密后的结果来拆除炸弹!
示例 1:
输入:code = [5,7,1,4], k = 3
输出:[12,10,16,13]
解释:每个数字都被接下来 3 个数字之和替换。解密后的密码为 [7+1+4, 1+4+5, 4+5+7, 5+7+1]。注意到数组是循环连接的。
示例 2:
输入:code = [1,2,3,4], k = 0
输出:[0,0,0,0]
解释:当 k 为 0 时,所有数字都被 0 替换。
示例 3:
输入:code = [2,4,9,3], k = -2
输出:[12,5,6,13]
解释:解密后的密码为 [3+9, 2+3, 4+2, 9+4] 。注意到数组是循环连接的。如果 k 是负数,那么和为 之前 的数字。
提示:
n == code.length
1 <= n <= 100
1 <= code[i] <= 100
-(n - 1) <= k <= n - 1
滑动窗口:
class Solution {
public:
vector<int> decrypt(vector<int>& code, int k) {
int n = code.size();
vector<int> res(n);
if (k == 0)
return res;
int start = 1, end = k, sum = 0;
if (k < 0) {
start = n + k;
end = n - 1;
}
for (int i = start; i <= end; i++) {
sum += code[i];
}
for (int i = 0; i < n; i++) {
res[i] = sum;
sum -= code[(start++ % n + n) % n];
sum += code[(++end % n + n) % n];
}
return res;
}
};
741. 摘樱桃(Hard)
给你一个 n x n 的网格 grid ,代表一块樱桃地,每个格子由以下三种数字的一种来表示:
0 表示这个格子是空的,所以你可以穿过它。
1 表示这个格子里装着一个樱桃,你可以摘到樱桃然后穿过它。
-1 表示这个格子里有荆棘,挡着你的路。
请你统计并返回:在遵守下列规则的情况下,能摘到的最多樱桃数:
从位置 (0, 0) 出发,最后到达 (n - 1, n - 1) ,只能向下或向右走,并且只能穿越有效的格子(即只可以穿过值为 0 或者 1 的格子);
当到达 (n - 1, n - 1) 后,你要继续走,直到返回到 (0, 0) ,只能向上或向左走,并且只能穿越有效的格子;
当你经过一个格子且这个格子包含一个樱桃时,你将摘到樱桃并且这个格子会变成空的(值变为 0 );
如果在 (0, 0) 和 (n - 1, n - 1) 之间不存在一条可经过的路径,则无法摘到任何一个樱桃。
示例 1:
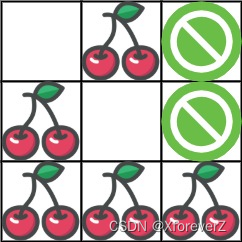
输入:grid = [[0,1,-1],[1,0,-1],[1,1,1]]
输出:5
解释:玩家从 (0, 0) 出发:向下、向下、向右、向右移动至 (2, 2) 。
在这一次行程中捡到 4 个樱桃,矩阵变成 [[0,1,-1],[0,0,-1],[0,0,0]] 。
然后,玩家向左、向上、向上、向左返回起点,再捡到 1 个樱桃。
总共捡到 5 个樱桃,这是最大可能值。
示例 2:
输入:grid = [[1,1,-1],[1,-1,1],[-1,1,1]]
输出:0
提示:
n == grid.length
n == grid[i].length
1 <= n <= 50
grid[i][j] 为 -1、0 或 1
grid[0][0] != -1
grid[n - 1][n - 1] != -1
经典DP:
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
vector<vector<vector<int>>> dp(
n, vector<vector<int>>(n, vector<int>(n, -1)));
return max(0, dfs(grid, dp, 0, 0, 0));
}
int dfs(vector<vector<int>>& grid, vector<vector<vector<int>>>& dp, int x1,
int y1, int x2) {
int y2 = x1 + y1 - x2;
if (x1 < 0 || y1 < 0 || x2 < 0 || y2 < 0 || x1 >= grid.size() ||
y1 >= grid.size() || x2 >= grid.size() || y2 >= grid.size() ||
grid[x1][y1] == -1 || grid[x2][y2] == -1) {
return -9999;
} else if (x1 == grid.size() - 1 && y1 == grid.size() - 1) {
return grid[x1][y1];
} else if (dp[x1][y1][x2] != -1) {
return dp[x1][y1][x2];
} else {
int ans = grid[x1][y1];
if (x1 != x2)
ans += grid[x2][y2];
ans += max(max(dfs(grid, dp, x1, y1 + 1, x2 + 1),
dfs(grid, dp, x1 + 1, y1, x2)),
max(dfs(grid, dp, x1, y1 + 1, x2),
dfs(grid, dp, x1 + 1, y1, x2 + 1)));
dp[x1][y1][x2] = ans;
return ans;
}
}
};
1463. 摘樱桃 II(Hard)
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。
你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。
请你按照如下规则,返回两个机器人能收集的最多樱桃数目:
从格子 (i,j) 出发,机器人可以移动到格子 (i+1, j-1),(i+1, j) 或者 (i+1, j+1) 。
当一个机器人经过某个格子时,它会把该格子内所有的樱桃都摘走,然后这个位置会变成空格子,即没有樱桃的格子。
当两个机器人同时到达同一个格子时,它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到 grid 外面。
两个机器人最后都要到达 grid 最底下一行。
示例 1:
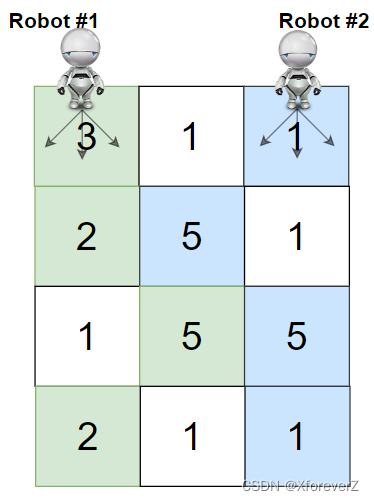
输入:grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出:24
解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为: 12 + 12 = 24 。
示例 2:
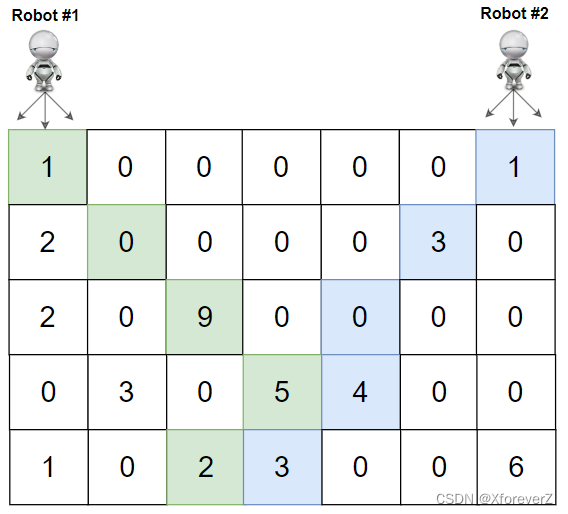
输入:grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出:28
解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为: 17 + 11 = 28 。
示例 3:
输入:grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出:22
示例 4:
输入:grid = [[1,1],[1,1]]
输出:4
提示:
rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100
又是DP:
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> f(n, vector<int>(n, -1)), g(n, vector<int>(n, -1));
f[0][n - 1] = grid[0][0] + grid[0][n - 1];
for (int i = 1; i < m; ++i) {
for (int j1 = 0; j1 < n; ++j1) {
for (int j2 = 0; j2 < n; ++j2) {
int best = -1;
for (int dj1 = j1 - 1; dj1 <= j1 + 1; ++dj1) {
for (int dj2 = j2 - 1; dj2 <= j2 + 1; ++dj2) {
if (dj1 >= 0 && dj1 < n && dj2 >= 0 && dj2 < n &&
f[dj1][dj2] != -1) {
best =
max(best, f[dj1][dj2] +
(j1 == j2 ? grid[i][j1]
: grid[i][j1] +
grid[i][j2]));
}
}
}
g[j1][j2] = best;
}
}
swap(f, g);
}
int ans = 0;
for (int j1 = 0; j1 < n; ++j1) {
for (int j2 = 0; j2 < n; ++j2) {
ans = max(ans, f[j1][j2]);
}
}
return ans;
}
};