一.排序
1.快速 排序 基于分治
- 确定分界点 左 右 中间 随机
- 划分区间 左半边<=x >=x在右半边
- 递归处理左右两端

#include<iostream>
using namespace std;
const int N = 1e6 +10;
int n;
int q[N];
void quick_sort(int q[],int l,int r)
{
if(l>=r)return;//边界:只有一个数,或者没有数 不用排序
int x=q[l],i=l-1,j=r+1; //1.确定分界点2。双指针指向边界的两侧 (只要因为指针调整交换往前移动一格)
while(i<j){
do i++;while(q[i]<x);
do j--;while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
quick_sort(q,0,n-1);
for(int i=0;i<n;i++) printf("%d",q[i]);
return 0;
}
2.归并—分治
二. 二分
1.确定分界点(中间下表)
2.递归排序左边和右边
3归并 把量有有序的数组合为一个
假设两个有效序列 两个指针指向开头 新数组来存答案
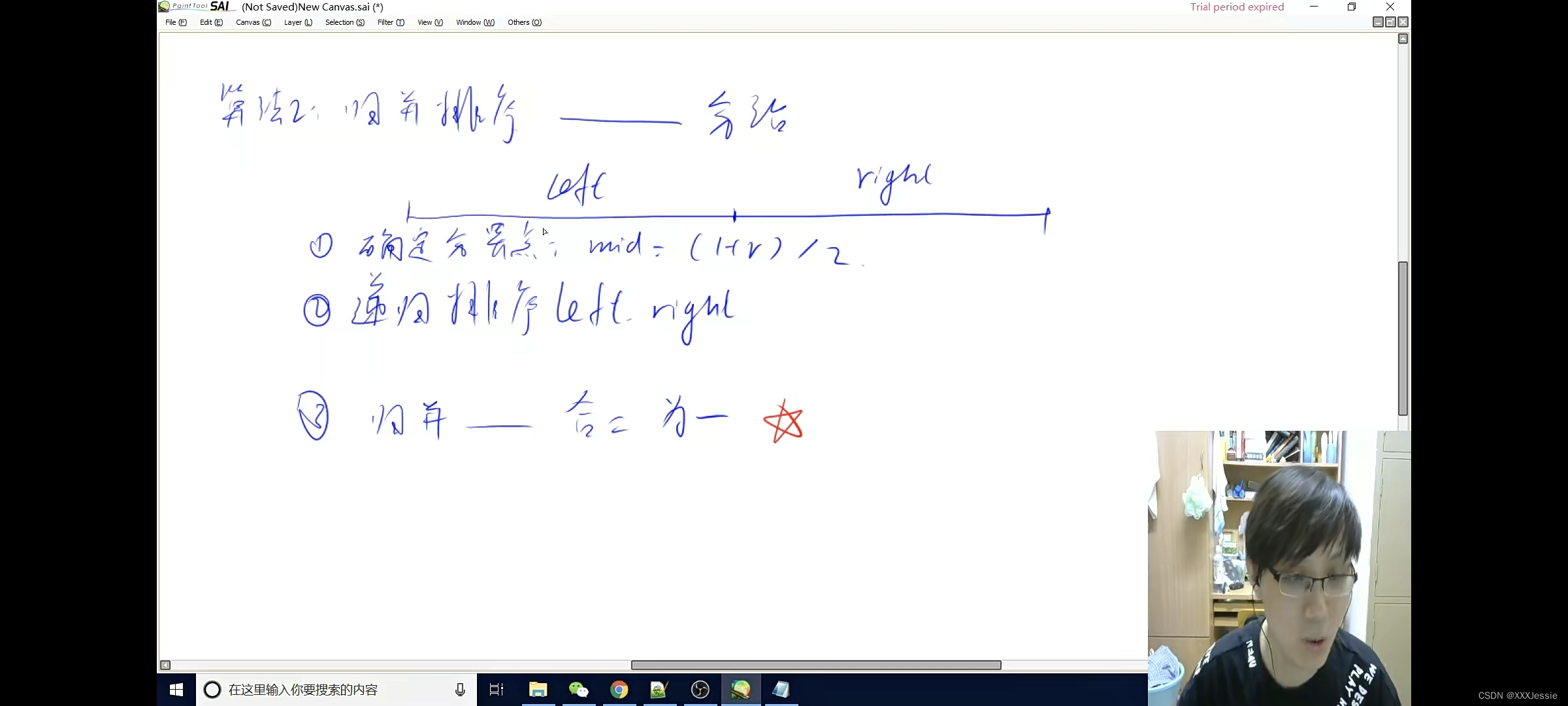
比较两个min 选择最小的微信数组的最小值 假设第一数更小 我们放到新的数组里 然后往后挪一位!
时间复杂度o(n)
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N], tmp[N];
void merge_sort(int q[], int l, int r) {
if (l >= r) return; // 递归边界
int mid = l + r >> 1;
merge_sort(q, l, mid); // 递归排序左半部分
merge_sort(q, mid + 1, r); // 递归排序右半部分
// 归并操作
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r) { // 合并
if (q[i] <= q[j]) {
tmp[k++] = q[i++];
} else {
tmp[k++] = q[j++];
}
}
while (i <= mid) { // 处理左半部分剩余元素
tmp[k++] = q[i++];
}
while (j <= r) { // 处理右半部分剩余元素
tmp[k++] = q[j++];
}
// 将排序后的部分复制回 q
for (int i = 0; i < k; i++) {
q[l + i] = tmp[i];
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &q[i]);
}
merge_sort(q, 0, n - 1);
for (int i = 0; i < n; i++) {
printf("%d ", q[i]); // 输出格式调整,添加空格
}
printf("\n"); // 输出换行
return 0;
}
整数二分
本质:有单调性一定可以二分 可以二分不一定就有单调性
如何选择用那个模板
给二分问题如何考虑 :1.写check 2.如何更新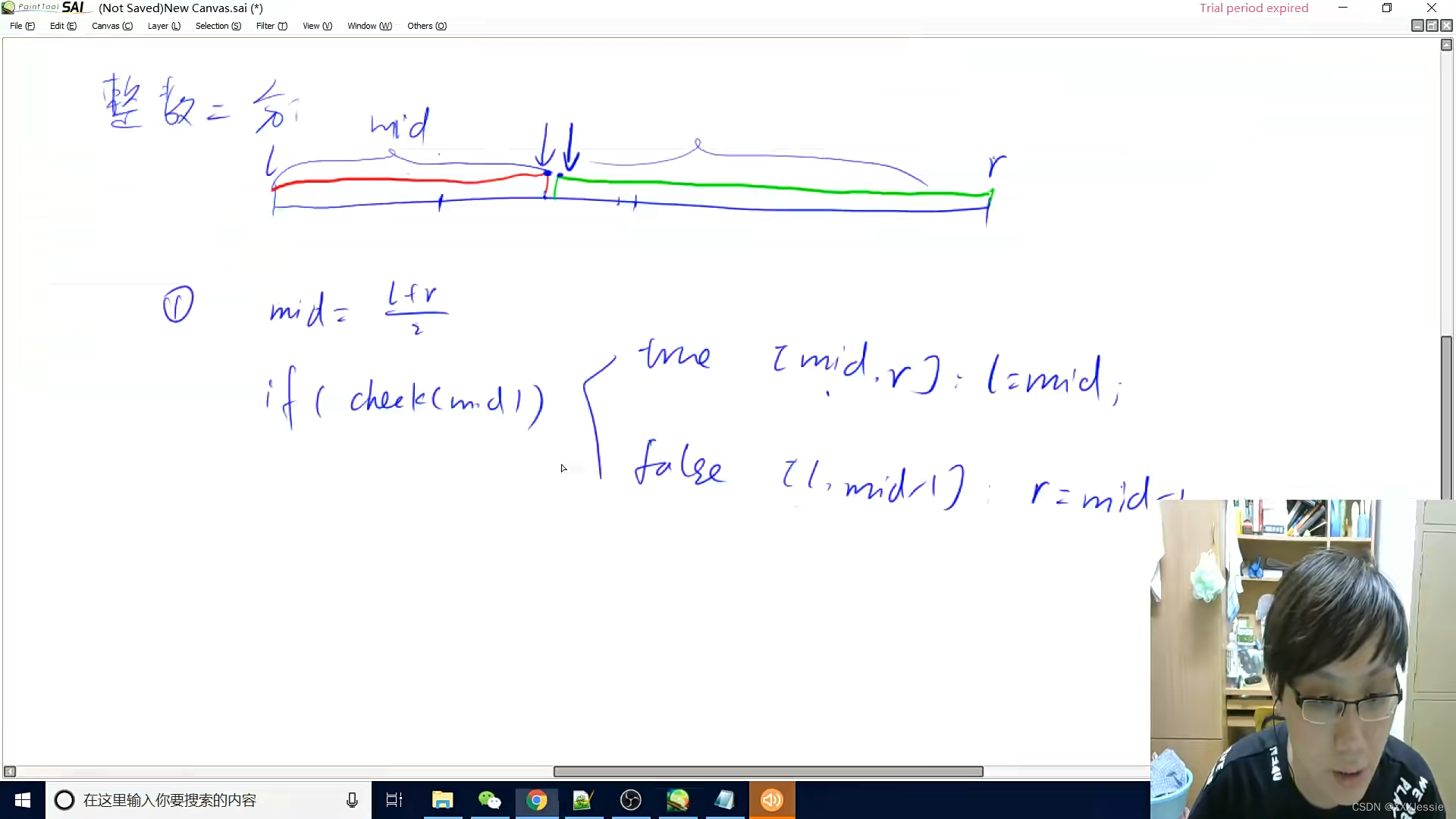
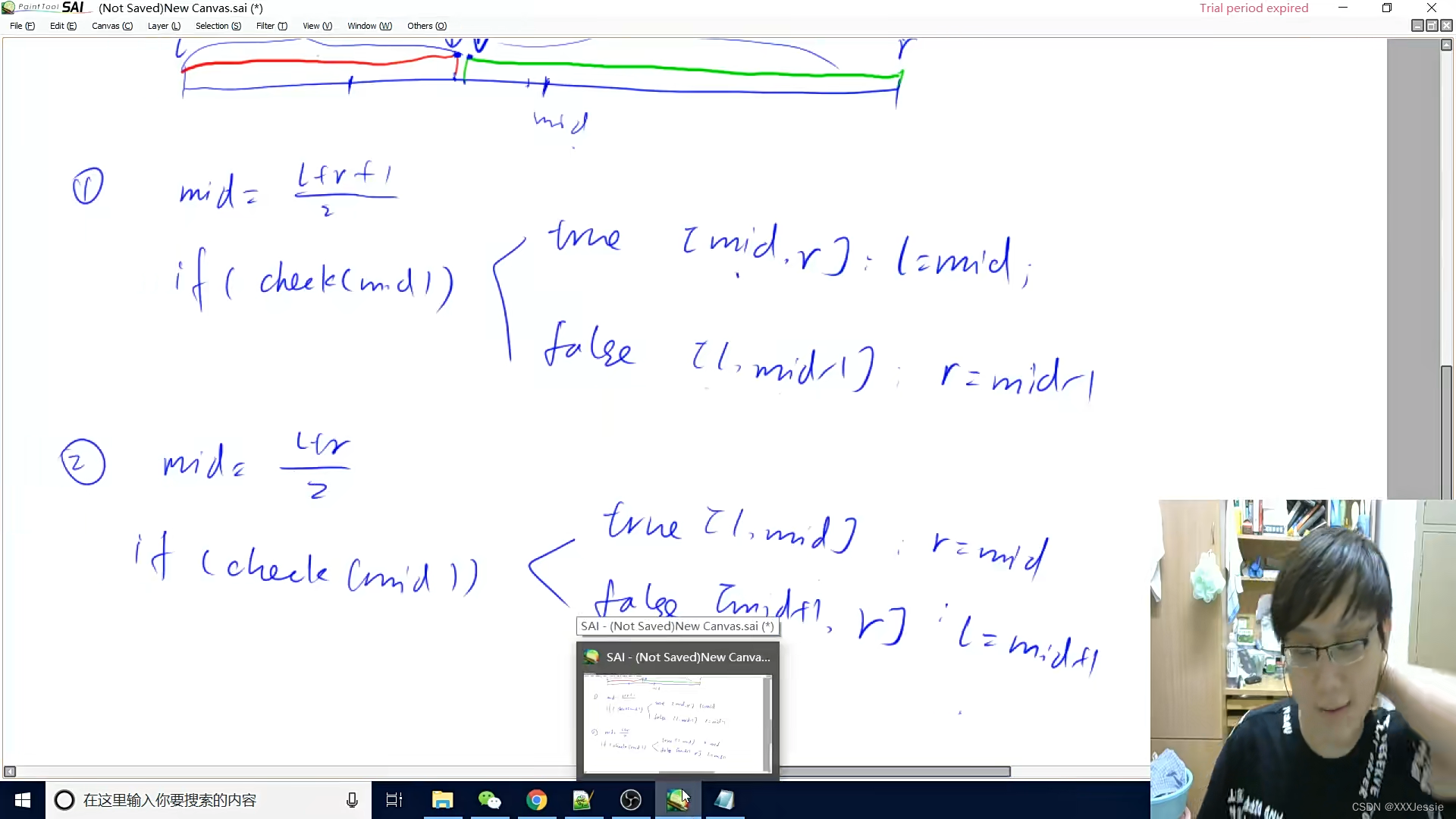
找mid 然后check函数