不存在负权边:
1.朴素dijkstra算法
原题:

思路:(依然是贪心的思想)
1.初始化距离:dis[1]=0,dis[i]=INF(正无穷)
2.循环n次:
找到当前不在s中的dis最小的点(s表示已经确定最短距离的点(可以开一个st数组表示))
假设找到了t这个点,用这个点更新其他所有点的最短距离:
if dis[x]>dis[t]+wi(这里wi表示边权)
实例演示:
代码如下:
一些注意细节(用//表示)
c++版本:
#include <iostream>
#include <cstring>
using namespace std;
const int N=510;
int q[N][N];
int dis[N];
int n,m;
bool st[N];
int dijkstra(){
memset(dis,0x3f,sizeof dis);
dis[1]=0;
for(int i=0;i<n-1;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||dis[t]>dis[j])){
//这里t==-1,其实代表是第一次进入,更新t的值,而后面才开始比较
t=j;
}
}
for(int j=1;j<=n;j++){
dis[j]=min(dis[j],dis[t]+q[t][j]);
}
st[t]=1;
}
if(dis[n]==0x3f3f3f3f) return -1;
return dis[n];
}
int main(){
cin>>n>>m;
memset(q,0x3f,sizeof q);
while(m--){
int x,y,z;
cin>>x>>y>>z;
q[x][y]=min(q[x][y],z);
}
cout<<dijkstra()<<" ";
return 0;
}
C:
#include <stdio.h>
#include <string.h>
#define N 510
int q[N][N];
int dis[N];
int n, m;
int st[N];
int min(int a, int b) {
return a < b ? a : b;
}
int dijkstra() {
memset(dis, 0x3f, sizeof(dis));
dis[1] = 0;
for (int i = 0; i < n - 1; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dis[t] > dis[j])) {
t = j;
}
}
for (int j = 1; j <= n; j++) {
dis[j] = min(dis[j], dis[t] + q[t][j]);
}
st[t] = 1;
}
if (dis[n] == 0x3f3f3f3f) return -1;
return dis[n];
}
int main() {
scanf("%d %d", &n, &m);
memset(q, 0x3f, sizeof(q));
while (m--) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
q[x][y] = min(q[x][y], z);
}
printf("%d ", dijkstra());
return 0;
}
python:
import sys
N = 510
q = [[float('inf')] * N for _ in range(N)] # 初始化邻接矩阵
dis = [float('inf')] * N # 初始化距离数组
st = [False] * N # 初始化标记数组
n, m = map(int, input().split()) # 读取节点数和边数
# 读取边的信息
for _ in range(m):
x, y, z = map(int, input().split())
q[x - 1][y - 1] = min(q[x - 1][y - 1], z) # 注意索引从0开始
def dijkstra():
dis[0] = 0 # 起始节点距离设为0
for _ in range(n - 1):
t = -1
for j in range(n):
if not st[j] and (t == -1 or dis[j] < dis[t]):
t = j
for j in range(n):
if q[t][j] != float('inf'):
dis[j] = min(dis[j], dis[t] + q[t][j])
st[t] = True
if dis[n - 1] == float('inf'):
return -1
return dis[n - 1]
print(dijkstra())Go:
package main
import (
"bufio"
"fmt"
"math"
"os"
"strconv"
"strings"
)
const N = 510
var (
q [N][N]int
dis [N]int
n int
m int
st = make([]bool, N)
)
func min(a, b int) int {
if a < b {
return a
}
return b
}
func dijkstra() int {
for i := range dis {
dis[i] = math.MaxInt32
}
dis[0] = 0 // 注意Go的数组索引从0开始
for i := 0; i < n; i++ {
t := -1
for j := 0; j < n; j++ {
if !st[j] && (t == -1 || dis[j] < dis[t]) {
t = j
}
}
for j := 0; j < n; j++ {
if q[t][j] != math.MaxInt32 {
dis[j] = min(dis[j], dis[t]+q[t][j])
}
}
st[t] = true
}
if dis[n-1] == math.MaxInt32 {
return -1 // 如果没有路径到达节点n-1
}
return dis[n-1]
}
func main() {
scanner := bufio.NewScanner(os.Stdin)
fmt.Scanln(&n, &m)
for i := range q {
for j := range q[i] {
q[i][j] = math.MaxInt32
}
}
for m > 0 {
m--
scanner.Scan()
line := scanner.Text()
fields := strings.Fields(line)
x, _ := strconv.Atoi(fields[0])
y, _ := strconv.Atoi(fields[1])
z, _ := strconv.Atoi(fields[2])
x-- // 转换为Go的索引
y--
q[x][y] = min(q[x][y], z)
}
fmt.Println(dijkstra())
}这里储存方式用邻接矩阵,主要是因为用于稠密图。图中可能存在重边和自环,但所有边权均为正值。算法复杂度:
2.堆优化的dijkstra
我们思考一下,上述步骤在哪里可以优化:找到当前不在s中的dis最小的点,我们可以用堆进行优化,优化后复杂度为:
,堆优化,手写堆和优先队列,但是其实在dijkstra中,不需要手写堆,两个复杂度差不多,不如用优先队列方便。并且,此时为稀疏图,用邻接表更好。
我们用邻接表现在只需要遍历邻接表中头元素连接的,进行更改,每一次取出队列中的最小值即可
C++:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e6 + 10;//注意开两倍大小
int h[N], w[N], e[N], ne[N], idx;
int n,m;
int dis[N];
bool st[N];
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<PII>> p;
void add(int a, int b, int c)//模板,记下来就好了
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra(){
memset(dis,0x3f,sizeof dis);
dis[1]=0;
p.push({0,1});
while(p.size()){
auto t=p.top();
p.pop();
int ver=t.second;
if(st[ver]) continue;//判断是否之前更新过了
st[ver]=1;
for(int i=h[ver];i!=-1;i=ne[i]){
int j=e[i];
if(dis[j]>dis[ver]+w[i]){
dis[j]=dis[ver]+w[i];
p.push({dis[j],j});
}
}
}
if(dis[n]==0x3f3f3f3f) return -1;
return dis[n];
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);//邻接表记得初始化头结点
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
cout<<dijkstra()<<" ";
return 0;
}
python:
import heapq
N = 1000010
h = [-1] * N
w = [0] * N
e = [0] * N
ne = [0] * N
idx = 0
n, m = map(int, input().split())
dis = [float('inf')] * N
st = [False] * N
p = []
def add(a, b, c):
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def dijkstra():
global dis
dis[1] = 0
heapq.heappush(p, (0, 1))
while p:
d, ver = heapq.heappop(p)
if st[ver]:
continue
st[ver] = True
i = h[ver]
while i != -1:
j = e[i]
if dis[j] > dis[ver] + w[i]:
dis[j] = dis[ver] + w[i]
heapq.heappush(p, (dis[j], j))
i = ne[i]
if dis[n] == float('inf'):
return -1
return dis[n]
for _ in range(m):
a, b, c = map(int, input().split())
add(a, b, c)
print(dijkstra())
如果存在负权边:
3.bellman-ford

对于边的存储方式不高。故可以用结构体初始化。
方式:初始化所有点到源点的距离为∞,把源点到自己的距离设置为0,遍历n次;每次遍历m条边,用每一条边去更新各点到源点的距离。在碰到限制了最短路径上边的长度时就只能用bellman_ford了。
for n次
for 所有边 a,b,w (松弛操作)
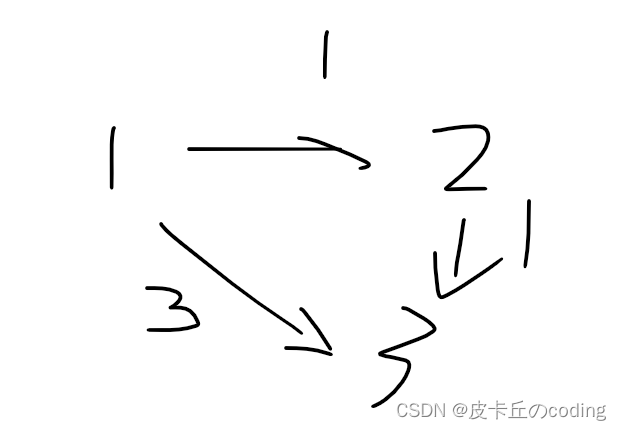
dis[b] = min(dis[b],back[a] + w)//注意:这里的backup非常重要,为了防止串联:(假设限制只能用1条边)
如下图:如果出现这样,不用之前的备份,就会出现1->3最近为2,而不是3,所以要备份一下之前的情况,用之前未更新的情况更新下一个节点。
c++:
#include<iostream>
#include <cstring>
using namespace std;
const int N=510,M=10010;
struct edge{
int a;
int b;
int w;
}edge[M];
int dis[N];
int backup[N];
int n,m,k;
void bellman_ford(){
memset(dis,0x3f,sizeof dis);
dis[1]=0;
for(int i=0;i<k;i++){
memcpy(backup,dis,sizeof dis);
for(int j=0;j<m;j++){
auto e=edge[j];
dis[e.b]=min(dis[e.b],backup[e.a]+e.w);
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=0;i<m;i++){
int x,y,z;
cin>>x>>y>>z;
edge[i]={x,y,z};
}
bellman_ford();
if(dis[n]>0x3f3f3f3f/2) puts("impossible");//可能存在负权边
else printf("%d\n", dis[n]);
return 0;
}c:
#include <stdio.h>
#include <string.h>
#define N 510
#define M 10010
struct Edge {
int a;
int b;
int w;
};
struct Edge edge[M];
int dis[N];
int backup[N];
int n, m, k;
void bellman_ford() {
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
for (int i = 0; i < k; i++) {
memcpy(backup, dis, sizeof dis);
for (int j = 0; j < m; j++) {
struct Edge e = edge[j];
if (backup[e.a] + e.w < dis[e.b]) {
dis[e.b] = backup[e.a] + e.w;
}
}
}
}
int main() {
scanf("%d %d %d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
edge[i].a = x;
edge[i].b = y;
edge[i].w = z;
}
bellman_ford();
if (dis[n] > 0x3f3f3f3f / 2) {
printf("impossible\n");
} else {
printf("%d\n", dis[n]);
}
return 0;
}
python:
N = 510
M = 10010
class Edge:
def __init__(self, a, b, w):
self.a = a
self.b = b
self.w = w
edge = [Edge(0, 0, 0) for _ in range(M)]
dis = [float('inf')] * N
backup = [0] * N
def bellman_ford():
global dis
dis[1] = 0
for _ in range(k):
backup[:] = dis[:]
for j in range(m):
e = edge[j]
dis[e.b] = min(dis[e.b], backup[e.a] + e.w)
def main():
global n, m, k
n, m, k = map(int, input().split())
for i in range(m):
x, y, z = map(int, input().split())
edge[i] = Edge(x, y, z)
bellman_ford()
if dis[n] > 0x3f3f3f3f // 2:
print("impossible")
else:
print(dis[n])
if __name__ == "__main__":
main()
Go:
package main
import (
"fmt"
)
const N = 510
const M = 10010
type Edge struct {
a, b, w int
}
var edge [M]Edge
var dis [N]int
var backup [N]int
var n, m, k int
func bellmanFord() {
for i := range dis {
dis[i] = 0x3f3f3f3f
}
dis[1] = 0
for i := 0; i < k; i++ {
copy(backup[:], dis[:])
for j := 0; j < m; j++ {
e := edge[j]
if dis[e.b] > backup[e.a]+e.w {
dis[e.b] = backup[e.a] + e.w
}
}
}
}
func main() {
fmt.Scan(&n, &m, &k)
for i := 0; i < m; i++ {
var x, y, z int
fmt.Scan(&x, &y, &z)
edge[i] = Edge{x, y, z}
}
bellmanFord()
if dis[n] > 0x3f3f3f3f/2 {
fmt.Println("impossible")
} else {
fmt.Println(dis[n])
}
}
时间复杂度:
4.spfa

对bellman-ford的优化,不一定每条边都会更新(spfa算法的想法基础)。
dis[b] = min(dis[b],back[a] + w)
观察这个式子,只有back[a]变小了,我的后继dis[b]才会变小
所以,我可以用一个队列,在一次变化中,只要有节点变小了,那么就肯定会影响后继节点,就放入队列之中。只要队列不空,就一直类似于bfs一样进行。
时间复杂度:一般,最坏
//与dijkstra非常相似
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
bool st[N];
queue<int> q;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa(){
memset(dis,0x3f,sizeof dis);
dis[1]=0;
q.push(1);
st[1]=1;
while(q.size()){
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dis[j]>dis[t]+w[i]){
dis[j]=dis[t]+w[i];
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
return dis[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int t = spfa();
if (t == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", t);
return 0;
}c:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>
#define N 100010
#define INF 0x3f3f3f3f
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
bool st[N];
typedef struct {
int data;
} QueueNode;
typedef struct {
QueueNode q[N];
int front, rear;
} Queue;
void initQueue(Queue *q) {
q->front = q->rear = 0;
}
bool isEmpty(Queue *q) {
return q->front == q->rear;
}
void enqueue(Queue *q, int x) {
q->q[q->rear].data = x;
q->rear = (q->rear + 1) % N; // 使用循环队列防止溢出
}
int dequeue(Queue *q) {
if (isEmpty(q)) return -1; // 队列为空,返回错误标识
int x = q->q[q->front].data;
q->front = (q->front + 1) % N;
return x;
}
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int spfa() {
memset(dis, INF, sizeof(dis));
dis[1] = 0;
Queue q;
initQueue(&q);
enqueue(&q, 1);
st[1] = true;
while (!isEmpty(&q)) {
int t = dequeue(&q);
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dis[j] > dis[t] + w[i]) {
dis[j] = dis[t] + w[i];
if (!st[j]) {
enqueue(&q, j);
st[j] = true;
}
}
}
}
return dis[n];
}
int main() {
scanf("%d%d", &n, &m);
memset(h, -1, sizeof(h));
while (m--) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int t = spfa();
if (t == INF) printf("impossible\n");
else printf("%d\n", t);
return 0;
}python:
from collections import deque
N = 100010
n, m = map(int, input().split())
h = [-1] * N
w = [0] * N
e = [0] * N
ne = [0] * N
dis = [float('inf')] * N
st = [False] * N
q = deque()
def add(a, b, c):
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def spfa():
global dis
dis[1] = 0
q.append(1)
st[1] = True
while q:
t = q.popleft()
st[t] = False
i = h[t]
while i != -1:
j = e[i]
if dis[j] > dis[t] + w[i]:
dis[j] = dis[t] + w[i]
if not st[j]:
q.append(j)
st[j] = True
i = ne[i]
return dis[n]
idx = 0
for _ in range(m):
a, b, c = map(int, input().split())
add(a, b, c)
t = spfa()
if t == float('inf'):
print("impossible")
else:
print(t)
5.spfa拓展:判断负环
原理:鸽笼原理+三角不等式
使用spfa算法解决是否存在负环问题
求负环的常用方法,基于SPFA,一般都用方法 2(该题也是用方法 2):
方法 1:统计每个点入队的次数,如果某个点入队n次,则说明存在负环
方法 2:统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于n,则也说明存在环
每次做一遍spfa()一定是正确的,但时间复杂度较高,可能会超时。初始时将所有点插入队列中可以按如下方式理解:
在原图的基础上新建一个虚拟源点,从该点向其他所有点连一条权值为0的有向边。那么原图有负环等价于新图有负环。此时在新图上做spfa,将虚拟源点加入队列中。然后进行spfa的第一次迭代,这时会将所有点的距离更新并将所有点插入队列中。执行到这一步,就等价于视频中的做法了。那么视频中的做法可以找到负环,等价于这次spfa可以找到负环,等价于新图有负环,等价于原图有负环。得证。1、dist[x] 记录虚拟源点到x的最短距离
2、cnt[x] 记录当前x点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为0,只要他能再走n步,即cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到x至少经过n条边时,则说明图中至少有n + 1个点,表示一定有点是重复使用
3、若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少,因此进行对该点j进行更新,并且对应cnt[j] = cnt[t] + 1,往前走一步
注意:该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点
引入一个cnt数组,记录每个点经过的边数
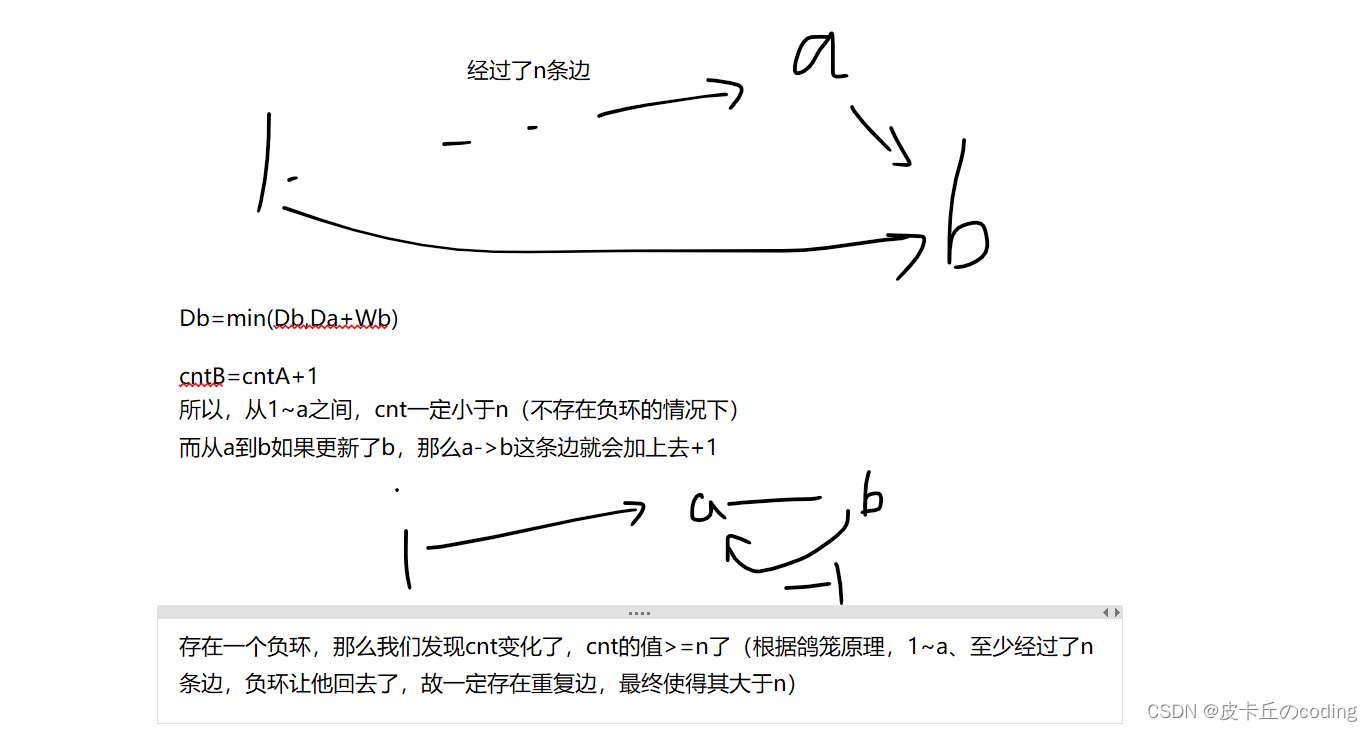
e.g.
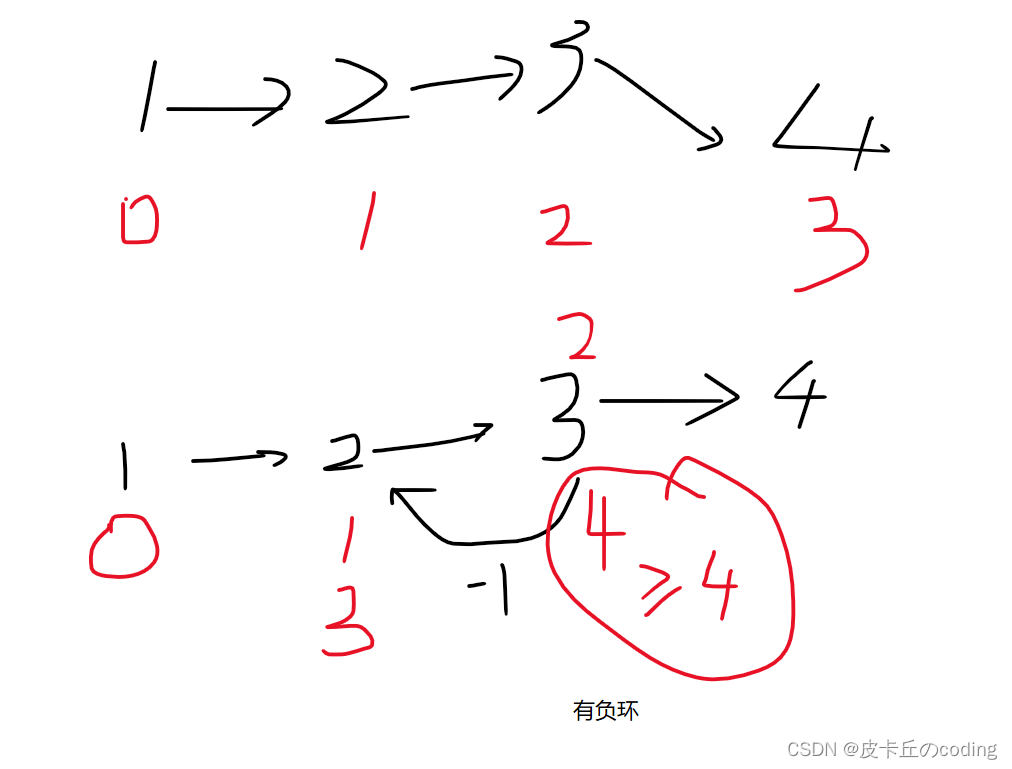
但是,如果从1开始到不了负环地方,那么就会出问题,我们的解决方法是一开始把所有的点都放入队列中:(本质就是以每个点为起点做一遍spfa)
for(int i=1;i<=n;i++){
st[i]=1;
q.push(i);
}
需要再cnt基础上更改的地方:
dis[j]=dis[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;还有对于cnt数组的初始化,还有把spfa变成布尔函数
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
int cnt[N];
bool st[N];
queue<int> q;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(){
memset(dis,0x3f,sizeof dis);
for(int i=1;i<=n;i++){
st[i]=1;
q.push(i);
}
dis[1]=0;
q.push(1);
st[1]=1;
while(q.size()){
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dis[j]>dis[t]+w[i]){
dis[j]=dis[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
if(spfa()) puts("Yes");
else puts("No");
return 0;
}多源汇最短路问题:
6.Floyd算法
原题:

原理:基于动态规划:
d[k,i,j]表示从第i个点出发到达j,只经过1~k个点的最短距离
状态转移方程:d[k,i,j]=d[k-1,i,k]+d[k-1,k,j]
发现:k与k-1刚好可以消去这个维度,用一个数组就可以实现
d[i,j]=d[i,k]+d[k,j]
算法时间复杂度:
具体:
假设节点序号是从1到n。
假设f[0][i][j]是一个n*n的矩阵,第i行第j列代表从i到j的权值,如果i到j有边,那么其值就为ci,j(边ij的权值)。
如果没有边,那么其值就为无穷大。f[k][i][j]代表(k的取值范围是从1到n),在考虑了从1到k的节点作为中间经过的节点时,从i到j的最短路径的长度。
比如,f[1][i][j]就代表了,在考虑了1节点作为中间经过的节点时,从i到j的最短路径的长度。
分析可知,f[1][i][j]的值无非就是两种情况,而现在需要分析的路径也无非两种情况,i->j,i->1->j:
【1】f[0][i][j]:i->j这种路径的长度,小于,i->1->j这种路径的长度
【2】f[0][i][1]+f[0][1][j]:i->1->j这种路径的长度,小于,i->j这种路径的长度
形式化说明如下:
f[k][i][j]可以从两种情况转移而来:
【1】从f[k−1][i][j]转移而来,表示i到j的最短路径不经过k这个节点
【2】从f[k−1][i][k]+f[k−1][k][j]转移而来,表示i到j的最短路径经过k这个节点总结就是:f[k][i][j]=min(f[k−1][i][j],f[k−1][i][k]+f[k−1][k][j])
从总结上来看,发现f[k]只可能与f[k−1]有关。
初始化与读入邻接矩阵(存在自环和重边的时候):
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
c++:
#include <iostream>
using namespace std;
const int N = 210, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &Q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
floyd();
while (Q -- )
{
int a, b;
scanf("%d%d", &a, &b);
int t = d[a][b];
if (t > INF / 2) puts("impossible");
else printf("%d\n", t);
}
return 0;
}
c:
#include <stdio.h>
#define N 210
#define INF 1000000000
int n, m, Q;
int d[N][N];
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (d[i][k] < INF && d[k][j] < INF) {
int new_dist = d[i][k] + d[k][j];
if (new_dist < d[i][j]) {
d[i][j] = new_dist;
}
}
}
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &Q);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) {
d[i][j] = 0;
} else {
d[i][j] = INF;
}
}
}
while (m--) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
if (c < d[a][b]) {
d[a][b] = c;
}
}
floyd();
while (Q--) {
int a, b;
scanf("%d%d", &a, &b);
int t = d[a][b];
if (t > INF / 2) {
puts("impossible");
} else {
printf("%d\n", t);
}
}
return 0;
}
java:
import java.util.Scanner;
public class Main {
static final int N = 210;
static final int INF = 1000000000;
static int n, m, Q;
static int[][] d = new int[N][N];
public static void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Q = scanner.nextInt();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
}
}
while (m-- > 0) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int c = scanner.nextInt();
d[a][b] = Math.min(d[a][b], c);
}
floyd();
while (Q-- > 0) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int t = d[a][b];
if (t > INF / 2) {
System.out.println("impossible");
} else {
System.out.println(t);
}
}
scanner.close();
}
}
python:
import sys
N = 210
INF = 10**9
def floyd():
global n, d
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
if __name__ == "__main__":
n, m, Q = map(int, input().split())
d = [[INF for _ in range(N)] for _ in range(N)]
for i in range(1, n+1):
d[i][i] = 0
for _ in range(m):
a, b, c = map(int, input().split())
d[a][b] = min(d[a][b], c)
floyd()
for _ in range(Q):
a, b = map(int, input().split())
t = d[a][b]
if t > INF // 2:
print("impossible")
else:
print(t)
Go语言:
package main
import "fmt"
const N = 210
const INF = 1000000000
var n, m, Q int
var d [N][N]int
func floyd() {
for k := 1; k <= n; k++ {
for i := 1; i <= n; i++ {
for j := 1; j <= n; j++ {
if d[i][k] < INF && d[k][j] < INF {
newDist := d[i][k] + d[k][j]
if newDist < d[i][j] {
d[i][j] = newDist
}
}
}
}
}
}
func main() {
fmt.Scanf("%d%d%d", &n, &m, &Q)
for i := 1; i <= n; i++ {
for j := 1; j <= n; j++ {
if i == j {
d[i][j] = 0
} else {
d[i][j] = INF
}
}
}
for m > 0 {
var a, b, c int
fmt.Scanf("%d%d%d", &a, &b, &c)
if c < d[a][b] {
d[a][b] = c
}
m--
}
floyd()
for Q > 0 {
var a, b int
fmt.Scanf("%d%d", &a, &b)
t := d[a][b]
if t > INF/2 {
fmt.Println("impossible")
} else {
fmt.Println(t)
}
Q--
}
}