文章目录
- 题目描述
- 算法原理
- 1.状态表示(题目+经验)
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值
- 代码实现
- C++
- Java
题目描述
题目链接:LCR 166.珠宝的最高价值

算法原理
1.状态表示(题目+经验)
对于这种路径类的问题,我们的状态表示⼀般有两种形式:
- 从 [i, j] 位置出发…
- 从起始位置出发,到达 [i, j] 位置…
这⾥选择第⼆种定义状态表示的方式:
dp[i][j] 表示:⾛到 [i, j] 位置处,此时珠宝的最大价值。
2.状态转移方程
根据最近的一步划分问题。对于 dp[i][j] ,我们发现想要到达 [i, j] 位置,有两种⽅式:
- 从 [i, j] 位置的上⽅ [i - 1, j] 位置,向下⾛⼀步,此时到达 [i, j] 位置能 拿到的礼物价值为 dp[i - 1][j] + frame[i][j] ;
- 从 [i, j] 位置的左边 [i, j - 1] 位置,向右⾛⼀步,此时到达 [i, j] 位置能 拿到的礼物价值为 dp[i][j - 1] + frame[i][j]
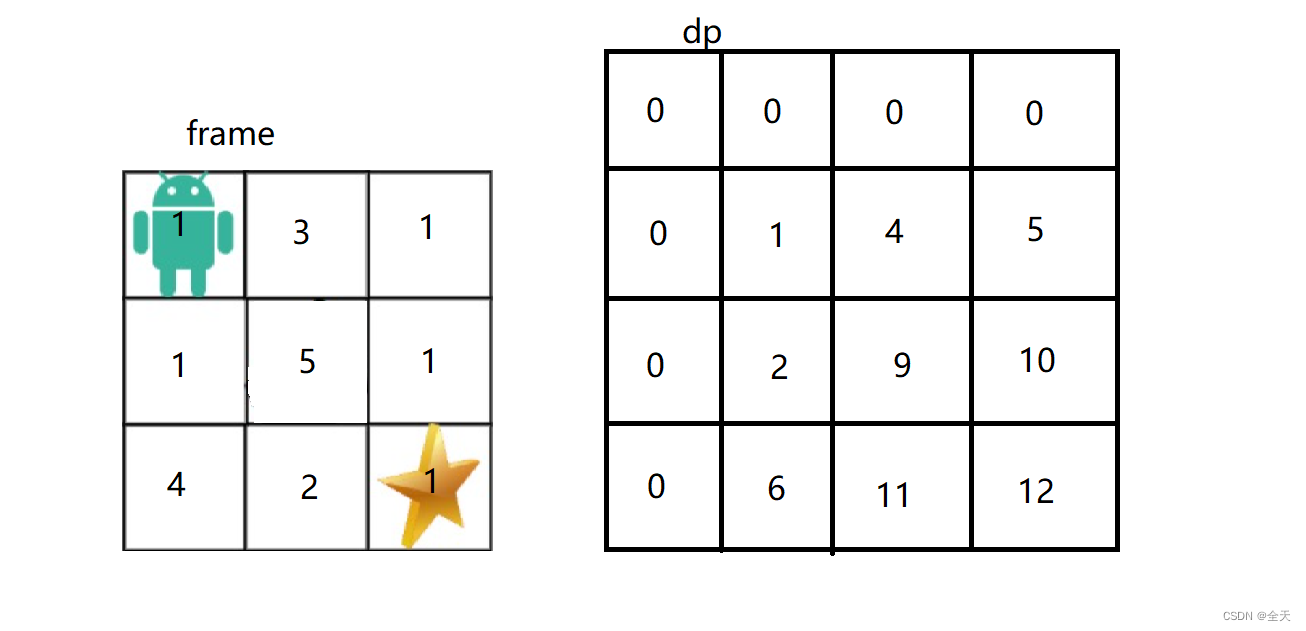
我们要的是最⼤值,因此状态转移方程为:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
3.初始化
可以在最前⾯加上⼀个辅助结点,帮助我们初始化。使⽤这种技巧要注意两个点:
- 辅助结点⾥⾯的值要保证后续填表是正确的;
- 下标的映射关系。
在本题中,添加一行,并且添加⼀列后,所有的值都为 0 即可。
4.填表顺序
根据状态转移方程,填表的顺序是从上往下填写每一行,每一行从左往右。
5.返回值
根据状态表示,我们应该返回 dp[m][n] 的值。
代码实现
C++
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
//1.创建一个dp表
int m = frame.size(), n = frame[0].size();
vector<vector<int>> dp(m + 1,vector<int>(n + 1));
//2.初始化
//3.填表
for(int i = 1;i <= m;++i)
for(int j = 1;j <= n;++j)
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
//4.返回值
return dp[m][n];
}
};
Java
class Solution {
public int jewelleryValue(int[][] frame) {
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
int m = frame.length, n = frame[0].length;
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]) + frame[i - 1][j - 1];
return dp[m][n];
}
}