目录
一,std容器
1,Vec(向量、栈)
2,VecDeque(队列、双端队列)
3,LinkedList(双向链表)
4,哈希表
5,集合
6,BinaryHeap(二叉堆、优先队列)
二,单向迭代器
1,Iterator特征、Iterator::next函数
2,IntoIterator特征、IntoIterator::into_iter函数
3,iter函数
4,iter_mut函数
5,Iterator::map函数
6,Iterator::collect函数、FromIterator特征
7,Iterator::cloned函数
8,小结
9,Iterator常用函数
(1)fold
10,Iterator常用函数2
11,Iterator常用函数3
三,双向迭代器
1,DoubleEndedIterator特征
2,Iterator::rev函数
一,std容器

1,Vec(向量、栈)
use std::vec::Vec;
(1)用作vector
let nums:Vec<i32>=vec![1,2,4,3];
assert_eq!(nums.len(),4);
assert_eq!(nums[3],3);
assert_eq!(nums.is_empty(),false);遍历:
let mut nums:Vec<i32>=vec![1,2,4,3];
for i in 0..nums.len() {
nums[i]=0;
}
assert_eq!(nums, vec![0,0,0,0]);
for x in nums.iter_mut(){
*x=1;
}
assert_eq!(nums, vec![1,1,1,1]);
for mut x in nums{
x=1;
}
// assert_eq!(nums, vec![1,1,1,1]); //error,nums丧失了所有权vector翻转:
fn vector_reverse<T:Clone> (v:&Vec<T>)->Vec<T>{
let mut ans = Vec::new();
let mut i = v.len();
loop {
if i==0{
break;
}
i-=1;
ans.push(v[i].clone());
}
return ans;
}(2)用作栈
let mut nums:Vec<i32>=Vec::new();
nums.push(123);
assert_eq!(nums.len(),1);
assert_eq!(nums.last(),Some(&123));
assert_eq!(nums.len(),1);
assert_eq!(nums.pop(),Some(123));
assert_eq!(nums.len(),0);(3)实现原理
pub(crate) struct RawVec<T, A: Allocator = Global> {
ptr: Unique<T>,
cap: usize,
alloc: A,
}
pub struct Vec<T, #[unstable(feature = "allocator_api", issue = "32838")] A: Allocator = Global> {
buf: RawVec<T, A>,
len: usize,
}buf中存放的是指针和最大可存储元素个数,len是实际元素个数。
例如push函数:
pub fn push(&mut self, value: T) {
if self.len == self.buf.capacity() {
self.buf.reserve_for_push(self.len);
}
unsafe {
let end = self.as_mut_ptr().add(self.len);
ptr::write(end, value);
self.len += 1;
}
}每次push都检查len和cap,扩容方案是倍增,同C++。
reserve函数:
pub fn reserve(&mut self, additional: usize) {
self.buf.reserve(self.len, additional);
}
let mut v = Vec::from([1]);
v.reserve(10);
assert_eq!(v.capacity(), 11);
assert_eq!(v.len(), 1);
Rust::reverse(n)等价于C++STL::reserve(n+ v.capacity())
resize函数:
pub fn resize(&mut self, new_len: usize, value: T) {
let len = self.len();
if new_len > len {
self.extend_with(new_len - len, value)
} else {
self.truncate(new_len);
}
}
let mut vec = vec!["hello"];
vec.resize(3, "world");
assert_eq!(vec, ["hello", "world", "world"]);
let mut vec = vec![1, 2, 3, 4];
vec.resize(2, 0);
assert_eq!(vec, [1, 2]);
resize函数和C++完全相同。
2,VecDeque(队列、双端队列)
use std::collections::VecDeque;
(1)用作队列
new创建空队列
len获取长度
with_capacity创建空队列 但 预占内存
push_back是尾部插入
pop_front是头部弹出,并获取弹出值
let deq:VecDeque<i32> = VecDeque::new();
assert_eq!(deq.len(), 0);
let mut deq:VecDeque<i32> = VecDeque::with_capacity(10);
assert_eq!(deq.len(), 0);
deq.push_back(1);
deq.push_back(2);
assert_eq!(deq.pop_front(),Some(1));
assert_eq!(deq.len(), 1);(2)用作双端队列
from从列表创建队列
get获取任意位置的值
push_front头部插入
pop_back尾部弹出,并获取弹出值
2个队列还可以直接比较
let mut deq = VecDeque::from([-1, 0, 1]);
assert_eq!(deq.get(2),Some(&1));
deq.push_front(2);
assert_eq!(deq.pop_back(),Some(1));
let deq2 = VecDeque::from([2, -1, 0]);
assert_eq!(deq,deq2);
deq.pop_back();
assert_ne!(deq,deq2);(3)实现原理
pub struct VecDeque<T,A: Allocator = Global,> {
head: usize,
len: usize,
buf: RawVec<T, A>,
}不像c++采用分段数组,rust的双端队列采用的是循环数组。
扩容方案:
fn grow(&mut self) {
// Extend or possibly remove this assertion when valid use-cases for growing the
// buffer without it being full emerge
debug_assert!(self.is_full());
let old_cap = self.capacity();
self.buf.reserve_for_push(old_cap);
unsafe {
self.handle_capacity_increase(old_cap);
}
debug_assert!(!self.is_full());
}和Vec一样,采用倍增的扩容方案。
这里的扩容稍微麻烦一点,先reserve_for_push倍增拷贝所有数据,然后handle_capacity_increase再拷贝部分数据(最多一半),调整head和tail
3,LinkedList(双向链表)
use std::collections::LinkedList;
(1)用法
支持在头部和尾部插入节点,在任意位置删除节点。
let mut list = LinkedList::new();
list.push_back(2);
list.push_back(3);
list.push_front(1);
// list is 1->2->3
assert_eq!(list.remove(1), 2);
assert_eq!(list.remove(0), 1);
assert_eq!(list.remove(0), 3);与其说这是双向链表,不如说这个有点像数组。
(2)源码
pub struct LinkedList<T, A: Allocator = Global,> {
head: Option<NonNull<Node<T>>>,
tail: Option<NonNull<Node<T>>>,
len: usize,
alloc: A,
marker: PhantomData<Box<Node<T>, A>>,
}
struct Node<T> {
next: Option<NonNull<Node<T>>>,
prev: Option<NonNull<Node<T>>>,
element: T,
}4,哈希表
use std::collections::HashMap;
use std::collections::BTreeMap;
2个哈希表的常用方法相同:
let mut m = HashMap::new();
if let Some(p) = m.get_mut(&1){
*p += 1;
}else{
m.insert(1, 1);
}
let mut m = BTreeMap::new();
if let Some(p) = m.get_mut(&1){
*p += 1;
}else{
m.insert(1, 1);
}例如,实现一个基于去重计数功能的类:
struct CalNum{
m:HashMap<i32,i32>,
}
impl CalNum{
fn add(& mut self,x:i32)->i32{
if let Some(p)=self.m.get_mut(&x){
*p+=1;
}else{
self.m.insert(x,1);
}
return self.m.len() as i32;
}
fn sub(& mut self,x:i32)->i32{
if let Some(p)=self.m.get_mut(&x){
*p-=1;
if *p <= 0{
self.m.remove(&x);
}
}
return self.m.len() as i32;
}
fn get(& mut self)->i32{
return self.m.len() as i32;
}
}5,集合
use std::collections::HashSet;
use std::collections::BTreeSet;
(1)常用方法
2个集合的常用方法完全相同。
HashSet:
let mut m = HashSet::new();
m.insert(5);
assert_eq!(m.len(), 1);
if !m.contains(&6) {
m.insert(6);
}
assert_eq!(m.len(), 2);
m.insert(6);
assert_eq!(m.len(), 2);
m.remove(&5);
m.remove(&6);
assert_eq!(m.is_empty(), true);BTreeSet:
let mut m = BTreeSet::new();
m.insert(5);
assert_eq!(m.len(), 1);
if !m.contains(&6) {
m.insert(6);
}
assert_eq!(m.len(), 2);
m.insert(6);
assert_eq!(m.len(), 2);
m.remove(&5);
m.remove(&6);
assert_eq!(m.is_empty(), true);(2)数据类型约束
impl<T, S> HashSet<T, S>
where
T: Eq + Hash,
S: BuildHasher,
{
......
}HashSet的泛型实现就约束了T具有Eq和Hash
impl<T, A: Allocator + Clone> BTreeSet<T, A> {
......
pub fn contains<Q: ?Sized>(&self, value: &Q) -> bool
where
T: Borrow<Q> + Ord,
Q: Ord,
{
self.map.contains_key(value)
}
......
pub fn insert(&mut self, value: T) -> bool
where
T: Ord,
{
self.map.insert(value, SetValZST::default()).is_none()
}
......
}BTreeSet的泛型实现约束较少,但是常见的接口需要Ord特征。
(3)浮点数示例
如果确保浮点数不会等于NAN,那么可以这么写:
#[derive(PartialEq,PartialOrd)]
struct FloatWithOrd{
x:f32, // do not let x be NAN
}
impl Eq for FloatWithOrd{
}
impl Ord for FloatWithOrd {
#[inline]
fn cmp(&self,other:&FloatWithOrd)->Ordering{
if(self.x < other.x){
return Ordering::Less;
}
if(self.x > other.x){
return Ordering::Greater;
}
return Ordering::Equal;
}
}
fn main() {
let mut m = BTreeSet::new();
m.insert(FloatWithOrd{x:5.0});
assert_eq!(m.len(), 1);
if !m.contains(&FloatWithOrd{x:6.0}) {
m.insert(FloatWithOrd{x:6.0});
}
assert_eq!(m.len(), 2);
m.insert(FloatWithOrd{x:6.0});
assert_eq!(m.len(), 2);
m.remove(&FloatWithOrd{x:5.0});
m.remove(&FloatWithOrd{x:6.0});
assert_eq!(m.is_empty(), true);
println!("end");
}浮点数类型的HashSet比较麻烦,需要Hash,暂时不研究这个。
6,BinaryHeap(二叉堆、优先队列)
use std::collections::BinaryHeap;
看实现源码是用二叉堆实现的。
默认堆顶是最大值:
let mut heap = BinaryHeap::new();
heap.push(1);
heap.push(3);
heap.push(1);
heap.push(2);
assert_eq!(heap.peek(),Some(&3));
heap.pop();
assert_eq!(heap.peek(),Some(&2));
heap.pop();
assert_eq!(heap.peek(),Some(&1));
heap.pop();
assert_eq!(heap.peek(),Some(&1));
heap.pop();
assert_eq!(heap.peek(),None);要想使用堆顶是最小值的堆,有2种方法:自定义序关系、reserve
(1)自定义序关系
#[derive(Eq,PartialEq)]
struct Node{
num:i32
}
impl Ord for Node {
#[inline]
fn cmp(&self,other:&Node)->Ordering{
return other.num.cmp(&self.num);
}
}
impl PartialOrd for Node {
#[inline]
fn partial_cmp(&self, other: &Node) -> Option<Ordering> {
return Some(self.cmp(other));
}
}
fn main() {
let mut heap = BinaryHeap::new();
heap.push(Node{num:1});
heap.push(Node{num:3});
assert_eq!(heap.peek().unwrap().num, 1);
println!("end");
}注意,自己实现PartialOrd但是Ord用默认的话,在堆里面的逻辑也是对的,但是以后如果有别人把这个结构体用于堆之外的场景,可能就有BUG了。
(2)用reserve
use std::cmp::Reverse;
fn main() {
let mut heap = BinaryHeap::new();
heap.push(Reverse(1));
heap.push(Reverse(3));
assert_eq!(heap.peek().unwrap(), &Reverse(1));
assert_eq!(Reverse(1)>Reverse(3), true);
println!("end");
}reserve就像是一个加负号的技巧:
fn main() {
let mut heap = BinaryHeap::new();
heap.push(-1);
heap.push(-3);
assert_eq!(heap.peek().unwrap(), &-1);
assert_eq!(-1>-3, true);
println!("end");
}(3)堆排序
BinaryHeap自带堆排序into_sorted_vec
(4)源码解析
虽然BinaryHeap的定义本身没有要求ord特征,但是默认实现的泛型方法要求了Ord特征。
这里我摘录了核心的几个函数:pop、push、into_sorted_vec,以及其中调用的关键操作。
pub struct BinaryHeap< T,A: Allocator = Global,> {
data: Vec<T, A>,
}
impl<T: Ord, A: Allocator> BinaryHeap<T, A> {
。。。。。。
pub fn pop(&mut self) -> Option<T> {
self.data.pop().map(|mut item| {
if !self.is_empty() {
swap(&mut item, &mut self.data[0]);
// SAFETY: !self.is_empty() means that self.len() > 0
unsafe { self.sift_down_to_bottom(0) };
}
item
})
}
pub fn push(&mut self, item: T) {
let old_len = self.len();
self.data.push(item);
// SAFETY: Since we pushed a new item it means that
// old_len = self.len() - 1 < self.len()
unsafe { self.sift_up(0, old_len) };
}
pub fn into_sorted_vec(mut self) -> Vec<T, A> {
let mut end = self.len();
while end > 1 {
end -= 1;
// SAFETY: `end` goes from `self.len() - 1` to 1 (both included),
// so it's always a valid index to access.
// It is safe to access index 0 (i.e. `ptr`), because
// 1 <= end < self.len(), which means self.len() >= 2.
unsafe {
let ptr = self.data.as_mut_ptr();
ptr::swap(ptr, ptr.add(end));
}
// SAFETY: `end` goes from `self.len() - 1` to 1 (both included) so:
// 0 < 1 <= end <= self.len() - 1 < self.len()
// Which means 0 < end and end < self.len().
unsafe { self.sift_down_range(0, end) };
}
self.into_vec()
}
unsafe fn sift_up(&mut self, start: usize, pos: usize) -> usize {
// Take out the value at `pos` and create a hole.
// SAFETY: The caller guarantees that pos < self.len()
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
while hole.pos() > start {
let parent = (hole.pos() - 1) / 2;
// SAFETY: hole.pos() > start >= 0, which means hole.pos() > 0
// and so hole.pos() - 1 can't underflow.
// This guarantees that parent < hole.pos() so
// it's a valid index and also != hole.pos().
if hole.element() <= unsafe { hole.get(parent) } {
break;
}
// SAFETY: Same as above
unsafe { hole.move_to(parent) };
}
hole.pos()
}
unsafe fn sift_down_range(&mut self, pos: usize, end: usize) {
// SAFETY: The caller guarantees that pos < end <= self.len().
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
let mut child = 2 * hole.pos() + 1;
// Loop invariant: child == 2 * hole.pos() + 1.
while child <= end.saturating_sub(2) {
// compare with the greater of the two children
// SAFETY: child < end - 1 < self.len() and
// child + 1 < end <= self.len(), so they're valid indexes.
// child == 2 * hole.pos() + 1 != hole.pos() and
// child + 1 == 2 * hole.pos() + 2 != hole.pos().
// FIXME: 2 * hole.pos() + 1 or 2 * hole.pos() + 2 could overflow
// if T is a ZST
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;
// if we are already in order, stop.
// SAFETY: child is now either the old child or the old child+1
// We already proven that both are < self.len() and != hole.pos()
if hole.element() >= unsafe { hole.get(child) } {
return;
}
// SAFETY: same as above.
unsafe { hole.move_to(child) };
child = 2 * hole.pos() + 1;
}
// SAFETY: && short circuit, which means that in the
// second condition it's already true that child == end - 1 < self.len().
if child == end - 1 && hole.element() < unsafe { hole.get(child) } {
// SAFETY: child is already proven to be a valid index and
// child == 2 * hole.pos() + 1 != hole.pos().
unsafe { hole.move_to(child) };
}
}
unsafe fn sift_down(&mut self, pos: usize) {
let len = self.len();
// SAFETY: pos < len is guaranteed by the caller and
// obviously len = self.len() <= self.len().
unsafe { self.sift_down_range(pos, len) };
}
unsafe fn sift_down_to_bottom(&mut self, mut pos: usize) {
let end = self.len();
let start = pos;
// SAFETY: The caller guarantees that pos < self.len().
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
let mut child = 2 * hole.pos() + 1;
// Loop invariant: child == 2 * hole.pos() + 1.
while child <= end.saturating_sub(2) {
// SAFETY: child < end - 1 < self.len() and
// child + 1 < end <= self.len(), so they're valid indexes.
// child == 2 * hole.pos() + 1 != hole.pos() and
// child + 1 == 2 * hole.pos() + 2 != hole.pos().
// FIXME: 2 * hole.pos() + 1 or 2 * hole.pos() + 2 could overflow
// if T is a ZST
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;
// SAFETY: Same as above
unsafe { hole.move_to(child) };
child = 2 * hole.pos() + 1;
}
if child == end - 1 {
// SAFETY: child == end - 1 < self.len(), so it's a valid index
// and child == 2 * hole.pos() + 1 != hole.pos().
unsafe { hole.move_to(child) };
}
pos = hole.pos();
drop(hole);
// SAFETY: pos is the position in the hole and was already proven
// to be a valid index.
unsafe { self.sift_up(start, pos) };
}
。。。。。。
}
sift_down_range是往下调整到指定id,主要用于堆排序
sift_down是往下调整到底,直接调用sift_down_range
sift_down_to_bottom是先往下调整到底,之后再往上调整到顶。
(5)应用实例
rust源码的注释中,给出了Dijkstra's shortest path algorithm作为示例,如何使用优先队列。
//use std::cmp::Ordering;
//use std::collections::BinaryHeap;
#[derive(Copy, Clone, Eq, PartialEq)]
struct State {
cost: usize,
position: usize,
}
// The priority queue depends on `Ord`.
// Explicitly implement the trait so the queue becomes a min-heap
// instead of a max-heap.
impl Ord for State {
fn cmp(&self, other: &Self) -> Ordering {
// Notice that the we flip the ordering on costs.
// In case of a tie we compare positions - this step is necessary
// to make implementations of `PartialEq` and `Ord` consistent.
other.cost.cmp(&self.cost)
.then_with(|| self.position.cmp(&other.position))
}
}
// `PartialOrd` needs to be implemented as well.
impl PartialOrd for State {
fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
Some(self.cmp(other))
}
}
// Each node is represented as a `usize`, for a shorter implementation.
struct Edge {
node: usize,
cost: usize,
}
// Dijkstra's shortest path algorithm.
// Start at `start` and use `dist` to track the current shortest distance
// to each node. This implementation isn't memory-efficient as it may leave duplicate
// nodes in the queue. It also uses `usize::MAX` as a sentinel value,
// for a simpler implementation.
fn shortest_path(adj_list: &Vec<Vec<Edge>>, start: usize, goal: usize) -> Option<usize> {
// dist[node] = current shortest distance from `start` to `node`
let mut dist: Vec<_> = (0..adj_list.len()).map(|_| usize::MAX).collect();
let mut heap = BinaryHeap::new();
// We're at `start`, with a zero cost
dist[start] = 0;
heap.push(State { cost: 0, position: start });
// Examine the frontier with lower cost nodes first (min-heap)
while let Some(State { cost, position }) = heap.pop() {
// Alternatively we could have continued to find all shortest paths
if position == goal { return Some(cost); }
// Important as we may have already found a better way
if cost > dist[position] { continue; }
// For each node we can reach, see if we can find a way with
// a lower cost going through this node
for edge in &adj_list[position] {
let next = State { cost: cost + edge.cost, position: edge.node };
// If so, add it to the frontier and continue
if next.cost < dist[next.position] {
heap.push(next);
// Relaxation, we have now found a better way
dist[next.position] = next.cost;
}
}
}
// Goal not reachable
None
}
fn main() {
// This is the directed graph we're going to use.
// The node numbers correspond to the different states,
// and the edge weights symbolize the cost of moving
// from one node to another.
// Note that the edges are one-way.
//
// 7
// +-----------------+
// | |
// v 1 2 | 2
// 0 -----> 1 -----> 3 ---> 4
// | ^ ^ ^
// | | 1 | |
// | | | 3 | 1
// +------> 2 -------+ |
// 10 | |
// +---------------+
//
// The graph is represented as an adjacency list where each index,
// corresponding to a node value, has a list of outgoing edges.
// Chosen for its efficiency.
let graph = vec![
// Node 0
vec![Edge { node: 2, cost: 10 },
Edge { node: 1, cost: 1 }],
// Node 1
vec![Edge { node: 3, cost: 2 }],
// Node 2
vec![Edge { node: 1, cost: 1 },
Edge { node: 3, cost: 3 },
Edge { node: 4, cost: 1 }],
// Node 3
vec![Edge { node: 0, cost: 7 },
Edge { node: 4, cost: 2 }],
// Node 4
vec![]];
assert_eq!(shortest_path(&graph, 0, 1), Some(1));
assert_eq!(shortest_path(&graph, 0, 3), Some(3));
assert_eq!(shortest_path(&graph, 3, 0), Some(7));
assert_eq!(shortest_path(&graph, 0, 4), Some(5));
assert_eq!(shortest_path(&graph, 4, 0), None);
println!("endend");
}二,单向迭代器
1,Iterator特征、Iterator::next函数
源码:
pub trait Iterator {
type Item;
fn next(&mut self) -> Option<Self::Item>;
......省略了一堆函数,下文有一些常用函数
}只有next函数是需要具体实现的,其他函数都直接用trait内的默认实现即可。
遍历方法:
let mut v = vec![1,0,3];
let mut it = v.into_iter();
assert_eq!(it.next(), Some(1));
assert_eq!(it.next(), Some(0));
assert_eq!(it.next(), Some(3));
assert_eq!(it.next(), None);
assert_eq!(it.next(), None);接下来,我们以Vec为例,看看3种迭代器的next函数都是怎么实现的。
2,IntoIterator特征、IntoIterator::into_iter函数
以这个代码为例:
fn main() {
let nums:Vec<i32>=vec![1,2,4,3];
let x=nums.into_iter().next();
}首先我们发现里面先用到这个trait:
pub trait IntoIterator {
type Item;
type IntoIter: Iterator<Item = Self::Item>;
fn into_iter(self) -> Self::IntoIter;
}那么再看看Vec的IntoIterator是怎么实现的:
impl<T, A: Allocator> IntoIterator for Vec<T, A> {
type Item = T;
type IntoIter = IntoIter<T, A>;
fn into_iter(self) -> Self::IntoIter {
unsafe {
let mut me = ManuallyDrop::new(self);
let alloc = ManuallyDrop::new(ptr::read(me.allocator()));
let begin = me.as_mut_ptr();
let end = if T::IS_ZST {
begin.wrapping_byte_add(me.len())
} else {
begin.add(me.len()) as *const T
};
let cap = me.buf.capacity();
IntoIter {
buf: NonNull::new_unchecked(begin),
phantom: PhantomData,
cap,
alloc,
ptr: begin,
end,
}
}
}
}也就是说,Vec的into_iter方法会返回一个IntoIter类型的结构体,其中ptr和end都是裸指针。
IntoIter结构体是一个直接实现了Iterator特征的结构体:
impl<T, A: Allocator> Iterator for IntoIter<T, A> {
type Item = T;
fn next(&mut self) -> Option<T> {
if self.ptr == self.end {
None
} else if T::IS_ZST {
// `ptr` has to stay where it is to remain aligned, so we reduce the length by 1 by
// reducing the `end`.
self.end = self.end.wrapping_byte_sub(1);
// Make up a value of this ZST.
Some(unsafe { mem::zeroed() })
} else {
let old = self.ptr;
self.ptr = unsafe { self.ptr.add(1) };
Some(unsafe { ptr::read(old) })
}
}
}迭代器都会默认实现IntoIterator:
impl<I: Iterator> IntoIterator for I {
type Item = I::Item;
type IntoIter = I;
#[inline]
fn into_iter(self) -> I {
self
}
}即迭代器再调用into_iter函数会得到自身。
3,iter函数
再看看这个代码:
fn main() {
let nums:Vec<i32>=vec![1,2,4,3];
let mut x=nums.iter().next();
}首先Vec做一个隐式转换,转换成切片slice:
impl<T, A: Allocator> ops::Deref for Vec<T, A> {
type Target = [T];
fn deref(&self) -> &[T] {
unsafe { slice::from_raw_parts(self.as_ptr(), self.len) }
}
}然后切片的源码中有iter函数:
impl<T> [T] {
pub fn iter(&self) -> Iter<'_, T> {
Iter::new(self)
}
pub fn iter_mut(&mut self) -> IterMut<'_, T> {
IterMut::new(self)
}
}iter函数返回一个Iter结构体
Iter结构体也实现了Iterator特征。
4,iter_mut函数
参考iter函数、Iter结构体。
5,Iterator::map函数
map函数把迭代器转化成Map结构体
fn map<B, F>(self, f: F) -> Map<Self, F>
where
Self: Sized,
F: FnMut(Self::Item) -> B,
{
Map::new(self, f)
}Map结构体也是迭代器,它也实现了Iterator特征。
Map结构体包含迭代器和算子2个成员:
pub struct Map<I, F> {
// Used for `SplitWhitespace` and `SplitAsciiWhitespace` `as_str` methods
pub(crate) iter: I,
f: F,
}6,Iterator::collect函数、FromIterator特征
Iterator::collect函数调用FromIterator::from_iter函数
fn collect<B: FromIterator<Self::Item>>(self) -> B
where
Self: Sized,
{
FromIterator::from_iter(self)
}对于3种迭代器,不知道用了什么机制,只有IntoIter迭代器可以调用collect得到容器本身,另外2种迭代器不能调用它。
let mut v = vec![1,2,3];
//let v:Vec<i32> = v.iter().collect();
//let v:Vec<i32> = v.iter_mut().collect();
let v:Vec<i32> = v.into_iter().collect();对于Map结构体,不知道用了什么机制,会把里面的迭代器成员萃取出来,逐个调用Map结构体的算子成员进行运算,最后收集得到容器。
let mut v = vec![1,2,3];
let v1:Vec<i32> = v.iter().map(|x| x+1).collect();
let v2:Vec<i32> = v.iter_mut().map(|x| *x+1).collect();
let v3:Vec<i32> = v.into_iter().map(|x| x+1).collect();7,Iterator::cloned函数
和map类型,调用cloned函数也会得到一个结构体
fn cloned<'a, T: 'a>(self) -> Cloned<Self>
where
Self: Sized + Iterator<Item = &'a T>,
T: Clone,
{
Cloned::new(self)
}Cloned结构体里面只有一个迭代器成员:
pub struct Cloned<I> {
it: I,
}应该是由于相同的萃取机制,经过cloned函数之后,迭代器就能collect了。
不知道用了什么机制,只有Iter迭代器才可以用cloned。
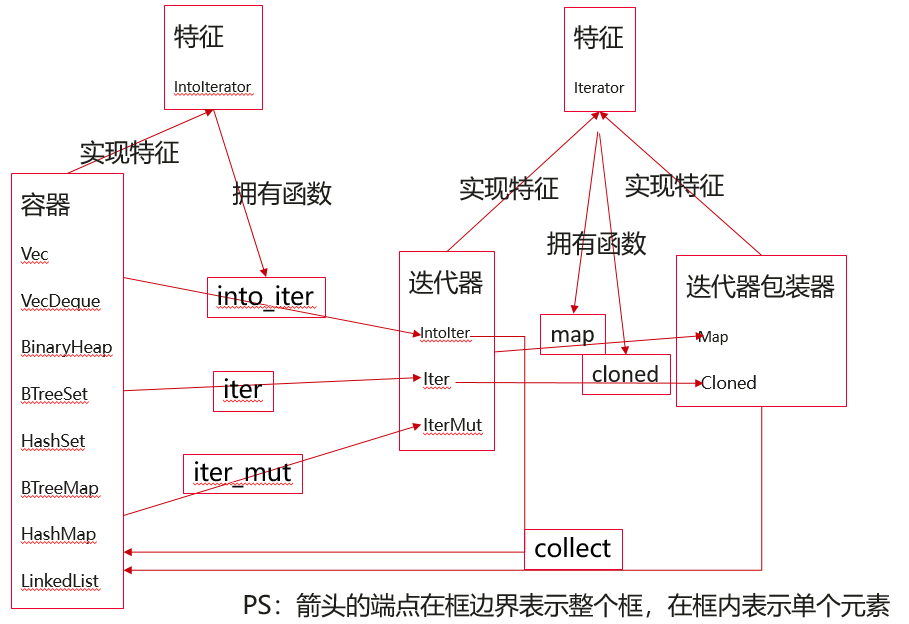
8,小结
9,Iterator常用函数
(1)fold
fn fold<B, F>(mut self, init: B, mut f: F) -> B
where
Self: Sized,
F: FnMut(B, Self::Item) -> B,
{
let mut accum = init;
while let Some(x) = self.next() {
accum = f(accum, x);
}
accum
}用来做累积运算,语法是:
iter.fold(init, |acc, x| {
// init是初始值
// acc是累积值,x是当前元素
// 返回更新后的acc
})例如,统计所有数的平方和:
let mut v = vec![1,2,3];
let x = v.iter().fold(0,|acc,x|{acc+x*x});
assert_eq!(x,14);10,Iterator常用函数2
fn for_each<F>(self, f: F) where Self: Sized, F: FnMut(Self::Item),
{
#[inline]
fn call<T>(mut f: impl FnMut(T)) -> impl FnMut((), T) {
move |(), item| f(item)
}
self.fold((), call(f));
}
fn filter<P>(self, predicate: P) -> Filter<Self, P> where Self: Sized, P: FnMut(&Self::Item) -> bool,
{
Filter::new(self, predicate)
}
fn skip(self, n: usize) -> Skip<Self> where Self: Sized,
{
Skip::new(self, n)
}
fn take(self, n: usize) -> Take<Self> where Self: Sized,
{
Take::new(self, n)
}
11,Iterator常用函数3
fn count(self) -> usize
where
Self: Sized,
{
self.fold(
0,
#[rustc_inherit_overflow_checks]
|count, _| count + 1,
)
}
fn last(self) -> Option<Self::Item>
where
Self: Sized,
{
#[inline]
fn some<T>(_: Option<T>, x: T) -> Option<T> {
Some(x)
}
self.fold(None, some)
}
fn zip<U>(self, other: U) -> Zip<Self, U::IntoIter>
where
Self: Sized,
U: IntoIterator,
{
Zip::new(self, other.into_iter())
}
fn unzip<A, B, FromA, FromB>(self) -> (FromA, FromB)
where
FromA: Default + Extend<A>,
FromB: Default + Extend<B>,
Self: Sized + Iterator<Item = (A, B)>,
{
let mut unzipped: (FromA, FromB) = Default::default();
unzipped.extend(self);
unzipped
}
fn max(self) -> Option<Self::Item>
where
Self: Sized,
Self::Item: Ord,
{
self.max_by(Ord::cmp)
}
fn min(self) -> Option<Self::Item>
where
Self: Sized,
Self::Item: Ord,
{
self.min_by(Ord::cmp)
}
fn sum<S>(self) -> S
where
Self: Sized,
S: Sum<Self::Item>,
{
Sum::sum(self)
}
fn product<P>(self) -> P
where
Self: Sized,
P: Product<Self::Item>,
{
Product::product(self)
}
fn copied<'a, T: 'a>(self) -> Copied<Self>
where
Self: Sized + Iterator<Item = &'a T>,
T: Copy,
{
Copied::new(self)
}
fn cloned<'a, T: 'a>(self) -> Cloned<Self>
where
Self: Sized + Iterator<Item = &'a T>,
T: Clone,
{
Cloned::new(self)
}
fn cmp<I>(self, other: I) -> Ordering
where
I: IntoIterator<Item = Self::Item>,
Self::Item: Ord,
Self: Sized,
{
self.cmp_by(other, |x, y| x.cmp(&y))
}
fn partial_cmp<I>(self, other: I) -> Option<Ordering>
where
I: IntoIterator,
Self::Item: PartialOrd<I::Item>,
Self: Sized,
{
self.partial_cmp_by(other, |x, y| x.partial_cmp(&y))
}
fn eq<I>(self, other: I) -> bool
where
I: IntoIterator,
Self::Item: PartialEq<I::Item>,
Self: Sized,
{
self.eq_by(other, |x, y| x == y)
}
fn ne<I>(self, other: I) -> bool
where
I: IntoIterator,
Self::Item: PartialEq<I::Item>,
Self: Sized,
{
!self.eq(other)
}还有其他很多函数没有列出来。
三,双向迭代器
1,DoubleEndedIterator特征
pub trait DoubleEndedIterator: Iterator {
fn next_back(&mut self) -> Option<Self::Item>;
......省略了几个函数
}双向迭代器DoubleEndedIterator特征 继承了 迭代器DoubleEndedIterator特征。
rust的容器都实现了DoubleEndedIterator特征
2,Iterator::rev函数
fn rev(self) -> Rev<Self> where Self: Sized + DoubleEndedIterator,
{
Rev::new(self)
}既然这个函数需要DoubleEndedIterator特征,为什么不把这个函数挪到DoubleEndedIterator特征里面?
根据stack_overflow中网友的解答,应该是出于使用方便的角度,因为容器是常用的,rev也是常用的,但DoubleEndedIterator特征是不太需要关注的。也就是说,这里面只有包管理、可见性相关的考量,并没有强逻辑的考量。
rev使用示例:
let mut v = vec![1,2,3];
let v:Vec<i32> = v.into_iter().rev().collect();
assert_eq!(v, vec![3,2,1]);