题目
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。
输入格式:
输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。
输出格式:
首先输出最小的辈分(老祖宗的辈分为 1,以下逐级递增)。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔,行首尾不得有多余空格。
输入样例:
9
2 6 5 5 -1 5 6 4 7
输出样例:
4
1 9
思路
感觉和无向图的并查集很相似都是找父母
//成员:1 2 3 4 5 6 7 8 9
//父母:2 6 5 5 -1 5 6 4 7
//第i个编号对应第i位成员的父母 == 第1个编号(即2) 对应第一位成员的父母
//第2个编号(即6)对应第二位成员的父母 == 2的父母为6
//3的父母是5,4的父母是5,5的父母为-1,6的父母是5
//最终形成图(最开始的5 的父母就是-1即祖宗,下面一次是它的儿女子孙,很像树,但不是二叉树,树的结点是父母,叶子是子女)
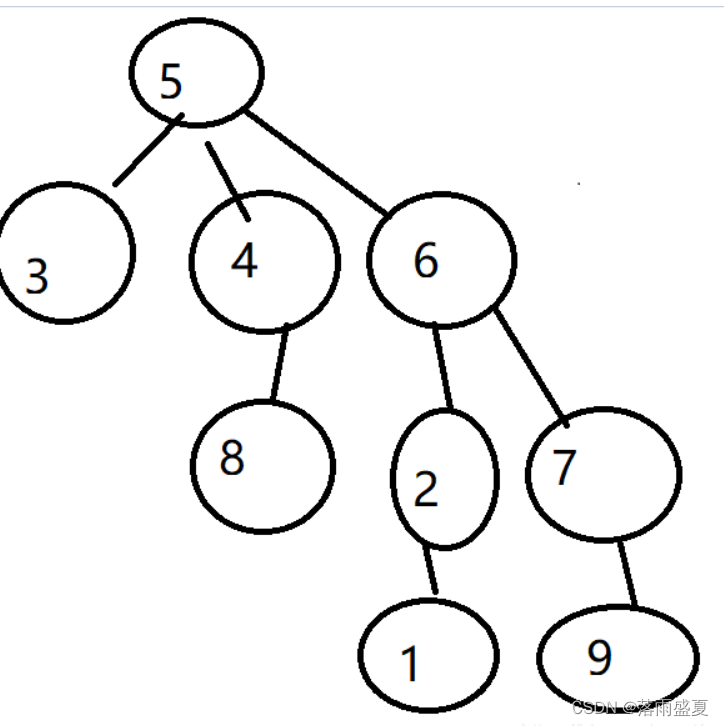
解题代码1
#include <iostream>
#define MAXN 10005
using namespace std;
int main(){
int N,p[MAXN],minG = maxG = 1//初始化最大最小辈分
int g[MAXN] = {0};//记录每个成员的辈分
int a[MAXN];
int count=0;
cin>>N;
for(int i = 1 ;i<= N ;i ++){
cin>>p[i];
//祖宗
if(p[i] = -1) countinue;
//确定父母的辈分
if(g[p[i]] == 0){
g[p[i]] == maxG + 1;
maxG++;
}
//更新儿女的辈分
g[i] = g[p[i]] + 1;
//更新最大辈分
if(g[i] > maxG) maxG = g[i];
if(g[i] < minG) minG = g[i];
}
//输出辈分数目
cout<<minG;
//找最小辈分存在哪些人
for(int i = 1; i<= N ;i ++){
if(g[i] == minG) m[count++] = i;
}
//输出最小辈分存在的人
for(int i = 0 ; i < count;i++){
cout<<m[i];
if(i < count-1) cout<<" ";
}
cout<<endl;
}
解题代码2
#include<iostream>
using namespace std;
int father[100000];
int beifen[100000] = {0};//所有人为0
int Find(int m){
if(father[m] == -1) //父母是祖宗
beifen[m] = 1;//辈分就是 1
else if(beifen[m] == 0)//辈分还未确定
beifen[m] = Find(father[m])+1; // 找父母的辈分,那自己的辈分是父母的+1
return beifen[m];
}
int main(){
int n,i,j;
int max = 0,flag = 0 , count = 0;
cin>>n;
for(i = 1 ; i <= n ; i++) cin>>father[i];//设置每个人是自己的父母
for( i = 1 ; i <= n ; i++)Find(i);//找父母
for( i = 1 ; i <= n ; i ++)//辈分更新
if(beifen[i]>max)
max = beifen[i];
cout<<max<<endl;//输出最大辈分
for( i = 1 ; i <= n ; i++) if(beifen[i] == max) count++;//记录辈分最大的人数
for( i = 1 ; i <= n ; i++){
if(beifen[i] == max){
if(flag == count - 1) cout<<i;//flag 计数确定最大辈分人的输出格式即确保最后有无空格
else {
cout<<i<<" ";
flag += 1;
}
}
}
cout<<endl;
}