文章目录
- 八数码
- 解题思路
- 图解举例
- 算法思路
- 代码
- CPP代码
- Java代码
八数码
在一个 3×3的网格中,1∼8这 8个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。
例如:
1 2 3
x 4 6
7 5 8
在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x
例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×3的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
输入样例:
2 3 4 1 5 x 7 6 8
输出样例
19
1、题目的目标

求最小步数 -> 用BFS
2、移动情况
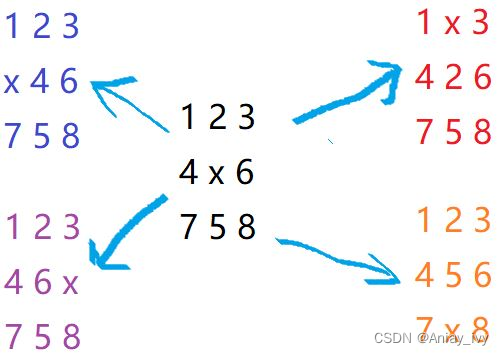
移动方式:
转以后:a = x + dx[i], b = y + dy[i].
思想:将每一种情况作为1个节点,目标情况即为终点
从初始状况移动到目标情况 —> 求最短路
3、问题
第一点:怎么表示一种情况使其能作为节点?
第二点:如何记录每一个状态的“距离”(即需要移动的次数)?
第三点:队列怎么定义,dist数组怎么定义?
4、解决方案
将 “3*3矩阵” 转化为 “字符串”
如:
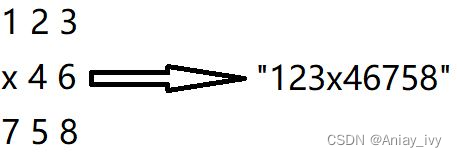
所以:
队列可以用 queue<string>
//直接存转化后的字符串
dist数组用 unordered_map<string, int>
//将字符串和数字联系在一起,字符串表示状态,数字表示距离
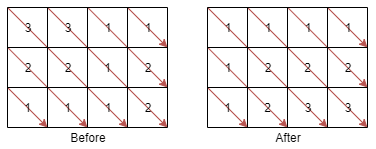
5、矩阵与字符串的转换方式

解题思路
暴力穷举。穷举出所有给定序列通过交换能得到的新序列,在穷举过程中保存交换次数。
在穷举过程中,如果出现了结果序列,就输出交换次数。
否则不能得到结果序列,输出 -1。
图解举例
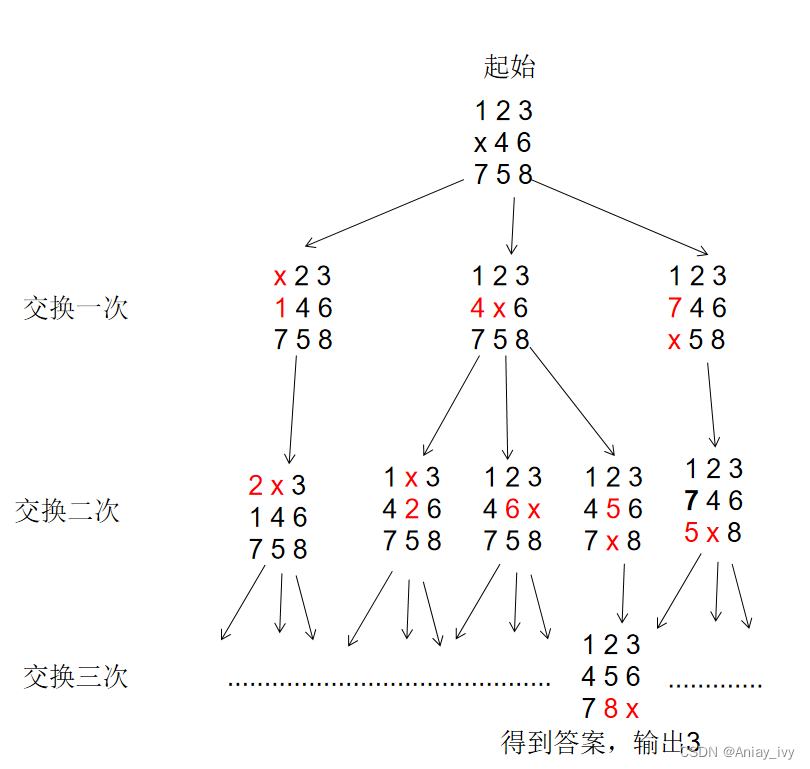
起始状态: 为 1 2 3 x 4 6 7 5 8
交换一次:
- x 与上方元素交换得到:
x 2 3 1 4 6 7 5 8 - x 与右方元素交换得到:
1 2 3 4 x 6 7 5 8 - x 与下方元素交换得到:
1 2 3 7 4 6 x 5 8
交换两次得到:
2 x 3 1 4 6 7 5 81 x 3 4 2 6 7 5 81 2 3 4 6 x 7 5 81 2 3 4 5 6 7 x 81 2 3 7 4 6 5 x 8
交换三次得到:
2 3 x 1 4 6 7 5 8- …
1 2 3 4 5 6 7 8 x- …
得到了最终结果,输出 3.
算法思路
- 用一个队列保存当前获得的序列
- 用一个哈希表保存各个序列与对应额交换次数。
- 从队列中取出队头这个序列,计算出这个序列通过交换能得到的序列。如果能到得的序列是个新序列(哈希表中没有这个序列),就把这个新序列放入队尾,哈希表中记录新序列对应的交换次数。
- 如果在上述过程中得到了结果序列,则输出交换次数,结束。
- 如果最终没有得到结果序列。输出-1。
代码
CPP代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;
// 保存各个序列
queue<string> q;
string s;
// 保存序列与对应的交换次数
unordered_map<string, int> h;
int main()
{
// 输入原始序列
for(int i = 1; i <= 9; i++)
{
char c;
cin >> c;
s += c;
}
// 保存初始状态
h[s] = 0;
q.push(s);
// 定义上下左右四个交换方向
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
// 依次进行交换
while(!q.empty())
{
// 获得当前序列
string t = q.front();
q.pop();
// 如果是最后结果,输出答案
if(t == "12345678x")
{
cout << h[t] << endl;
return 0;
}
// 找到 x 的位置
int pos = t.find('x');
// 计算 x 的坐标
int a = pos /3 , b = pos % 3 ;
// 获取当前序列对应的交换次数
int dist = h[t];
// 尝试和四个方向的元素进行交换
for(int i = 0; i < 4; i++)
{
int x = a + dx[i], y = b + dy[i];
// 判断是否越界
if(x >= 0 && x <= 2 && y >= 0 && y <= 2)
{
// 交换
swap(t[pos], t[3 * x + y]);
// 如果是个新序列,就保存新序列和对应的交换次数
if(h.find(t) == h.end())
{
h[t] = dist + 1;
q.push(t);
}
// 恢复现场,进行下一个方向的交换
swap(t[pos], t[3 * x + y]);
}
}
}
// 没有得到结果序列,输出-1
cout << -1;
return 0;
}
Java代码
import java.util.*;
public class Main{
public static void swap(char[] arr,int x,int y){
char temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
public static int bfs(String start ,String end){
Map<String,Integer> map = new HashMap<>();// 用来存储每种方式走过的距离
Queue<String> q = new LinkedList<>();//队列,用来存储内容
q.offer(start);//将初试元素插入到队列的尾部
map.put(start,0);//将初始状态的值对应map中value值对应0;表示还没有进行前进;
int[] dx = {-1,0,1,0},dy = {0,1,0,-1};//表示前进方向;上下左右
//如果队列不是空的继续循环
while(!q.isEmpty()){
String t = q.poll();//将队头元素返回并抛出
int k = t.indexOf('x');//找到x再String中的下标
int x = k / 3 ; int y = k % 3;//然后进行以为数组转化成二维的操作下标操作
if(t.equals(end)) return map.get(t); //如果进行过程中跟结束end相同的就提前结束
for(int i = 0 ; i < 4 ; i ++ ){//这里进行四种方案
int a = x + dx[i],b = y + dy[i];
if(a >= 0 && a < 3 && b >= 0 && b < 3){ //如果这种情况没有超出边界
//将这种情况的字符串转化成字符数组,能够有下标进行交换
char[] arr = t.toCharArray();
//然后交换x跟没有超出边界的值进行交换,二维转成一维下标x*3+y;
swap(arr, k, a * 3 + b);
//然后将字符数组转化成字符串
String str = new String(arr);
if(map.get(str) == null){ //如果这种情况对应的value值是null,说明还没有走过
map.put(str,map.get(t) + 1);//然后将这种情况对应进行上一步的距离加上1
q.offer(str);//然后将新的情况插入到队尾中
}
}
//思路:
//比如走到距离为2即第二步时候,上下左右四种情况都可行的情况下,将每一中情况都
//插入到队列尾部,然后queue[] = {2[1],2[1],2[1],2[1],3[1],3[1],3[2],3[4]};
//队列会执行从前面开始2执行完之后可能会有3种情况往队列尾插入,
//然后这样依次每一层进行搜索遍历
//因为步数小的都会先插入到队列中,队列原则"先进先出"原则,所以肯定会把所有的
//第二步执行完之后才会执行前面第二步执行过程中产生的三步,然后一直执行到最后第n步
}
}
return -1; //如果执行完之后没有结果,那么返回-1;
}
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
String start = "";
for(int i = 0 ; i < 9 ; i ++ ){
String s = scan.next();
start += s;
}
String end = "12345678x";
System.out.println(bfs(start,end));
}
}