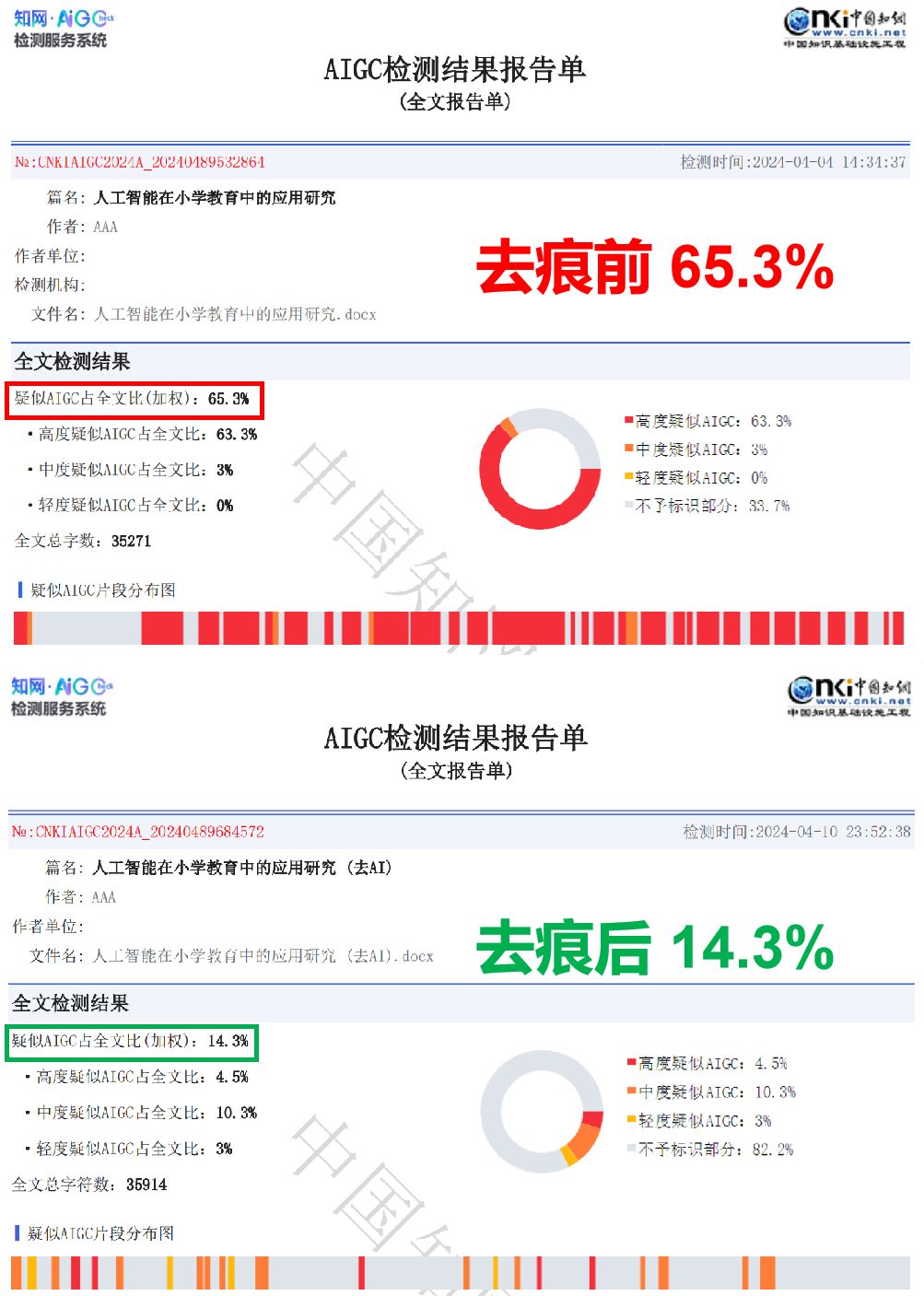
1.是什么：

针对机器学习提供了数据预处理，分类，回归等常见算法的框架

2.基于scikit-learn求解线性回归的问题：

2.1.求解a，b对新数据进行预测：

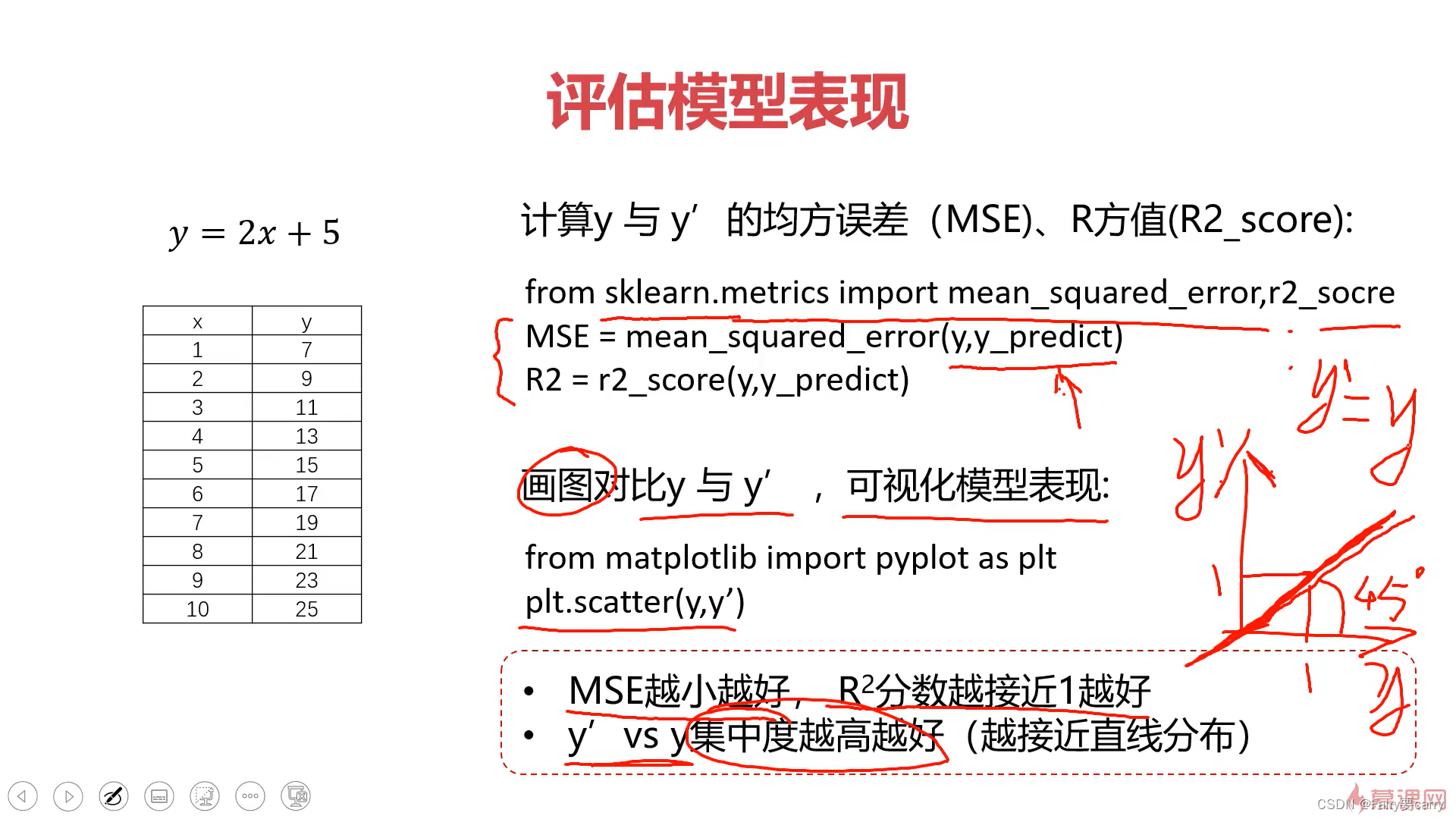
2.2评估模型表现（y和y’的方差MSE）：

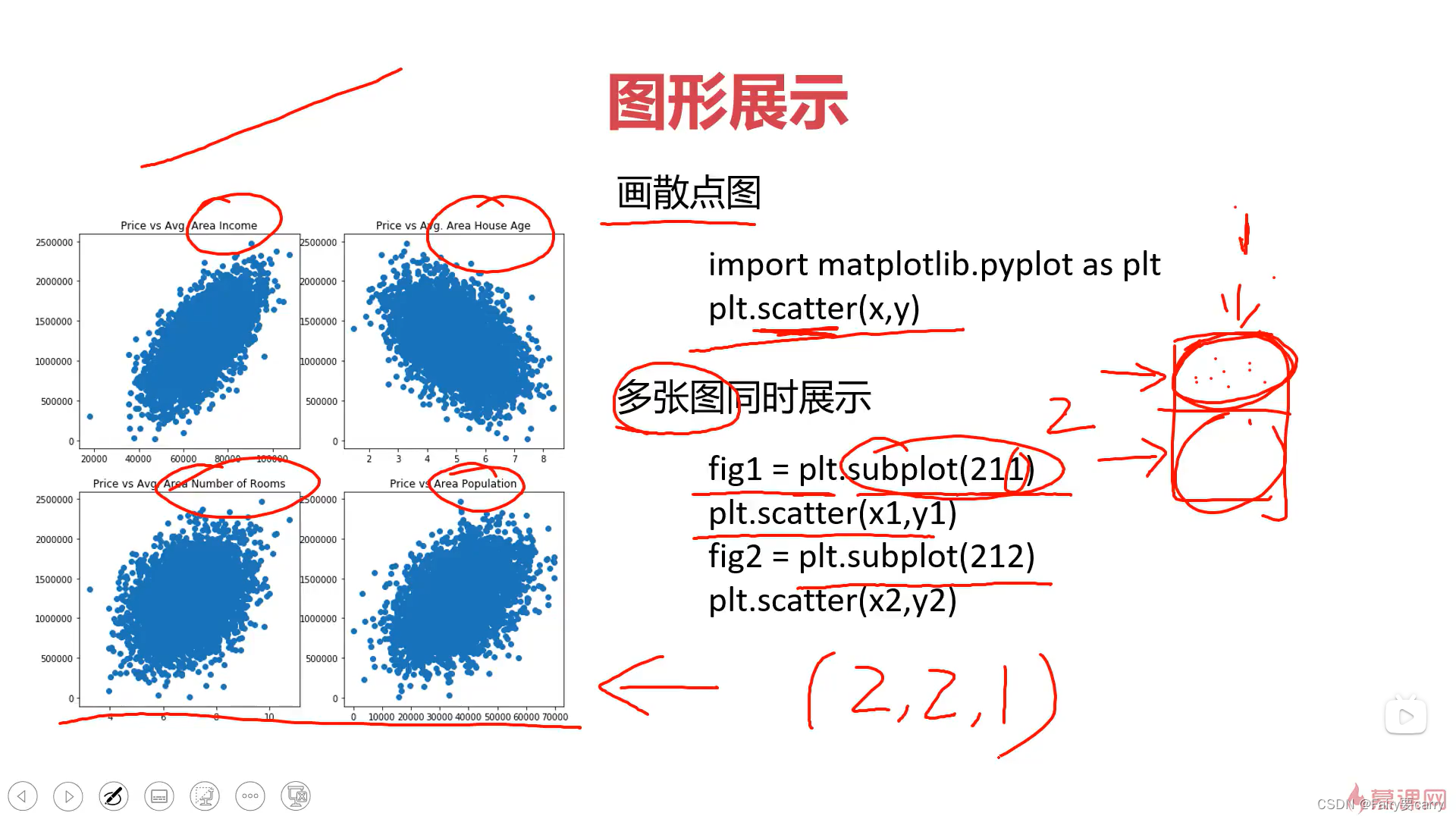
2.3 图形展示：

**scatter(x,y)：**画散点图
**绘画子图：**利用matplotlib绘画子图subplot(211)——>代表两行一列第一张图绘制

3.单因子线性回归模型：

1. 这些是导入所需的Python库和模块。NumPy用于数值计算，Pandas用于数据处理，Matplotlib用于绘图，而Scikit-learn中的LinearRegression类和评估指标用于线性回归建模和评估。
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
   10.

问：为什么scikit-learn期待输入的是二维数组？

1. 一致性： Scikit-learn的设计遵循一致性原则，即无论输入是一维数组还是二维数组，模型的处理方式应该是一致的。因此，为了保持一致性，大多数模型都要求输入是二维数组。
2. 多特征支持： 在实际问题中，往往会有多个特征（或自变量）影响目标变量（或因变量）。而使用二维数组可以很容易地表示多个特征，每一列代表一个特征，每一行代表一个样本。
3. 适应性： 使用二维数组可以更好地适应各种数据集的情况，不论是单特征还是多特征的情况。

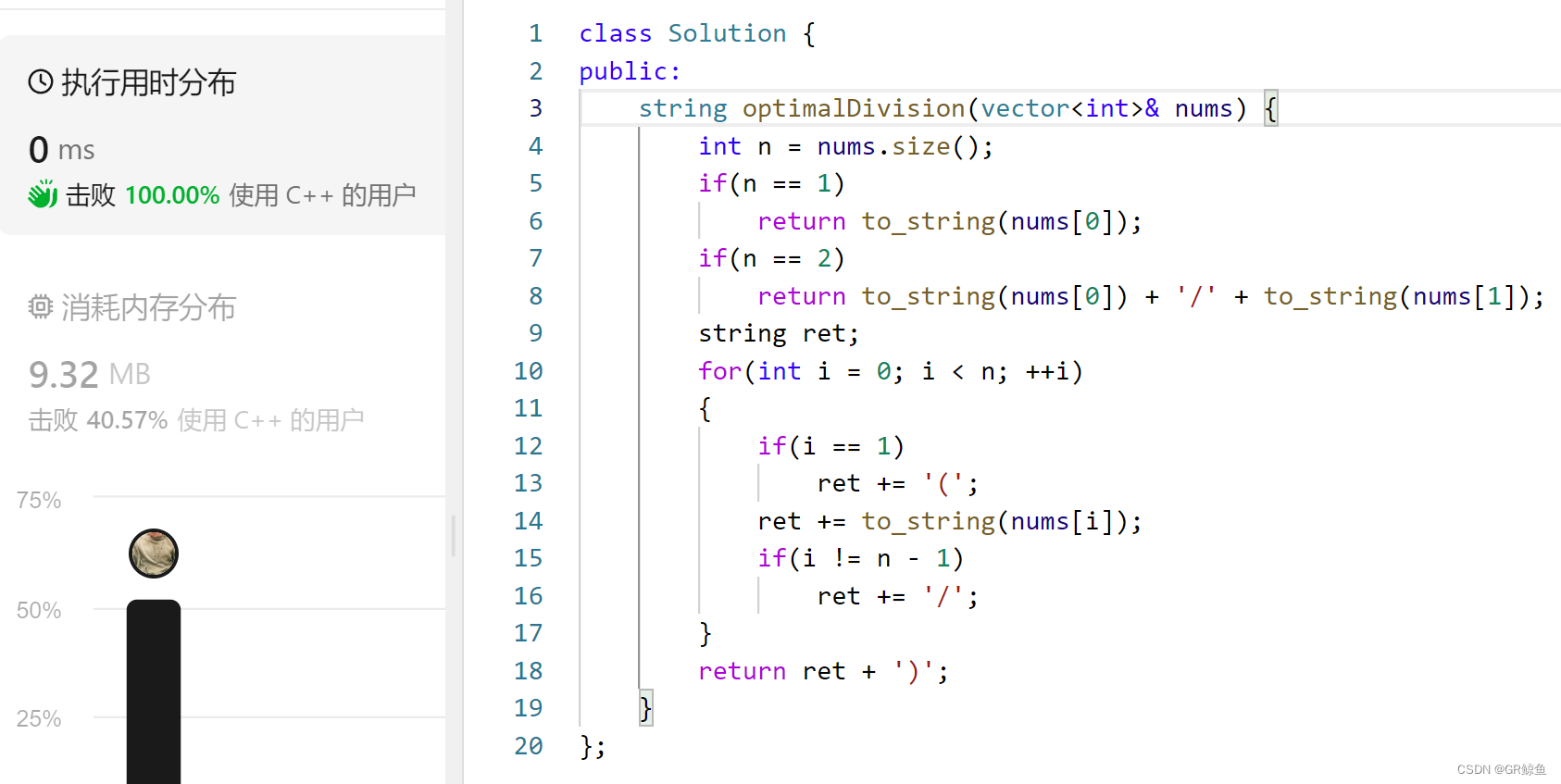
完整代码：

# 导入工具包
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

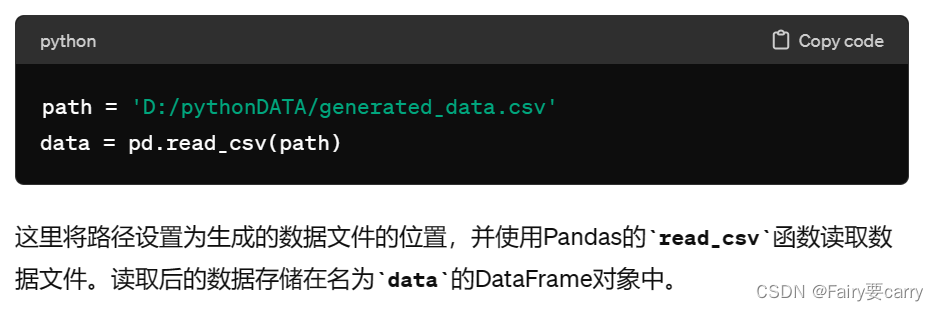
# 1.读取generated_data.csv文件数据
path = 'D:/pythonDATA/generated_data.csv'
data = pd.read_csv(path)
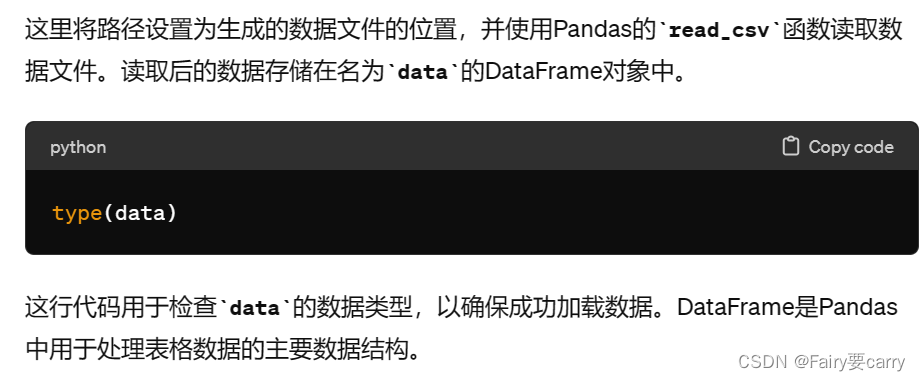
type(data)
# 2.查看读取到的文件
print(data.head())
# 3.分别将数据赋值给x和y
X = data['x']
y = data['y']
print(type(X))
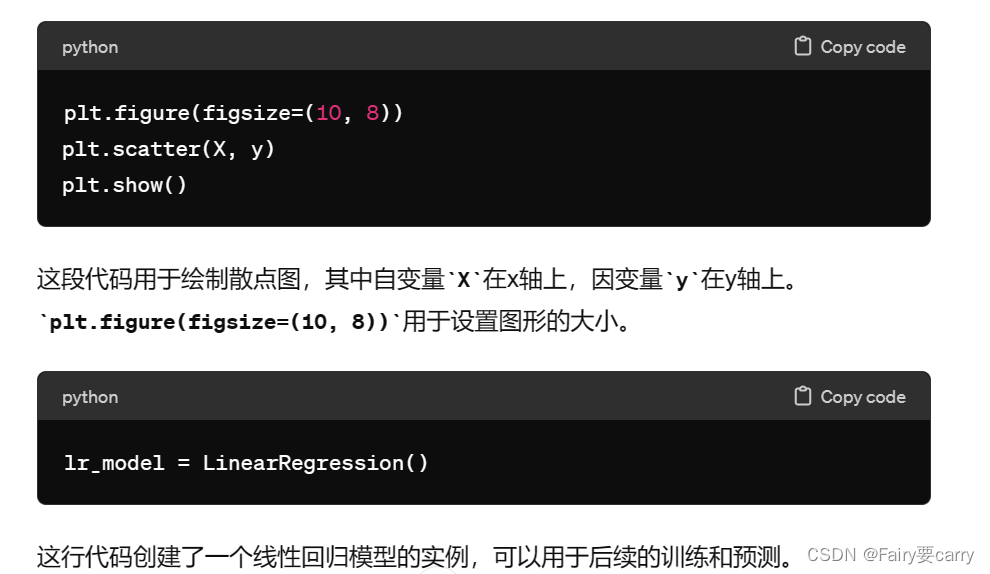
# 4.利用matplotlip将数据可视化，进行分散图显示
plt.figure(figsize=(10, 8))
plt.scatter(X, y)
plt.show()
# 5.创造线性回归模型
lr_model = LinearRegression()
# 输出X的纬度
print(X.shape)
# 6.先将X利用numpy转为数组，然后再reshape成二维数组
X = np.array(X)
print(X)
X = X.reshape(-1, 1)
print(X)
print(X.shape)  # (10,1)
# 7.拟合训练
lr_model.fit(X, y)
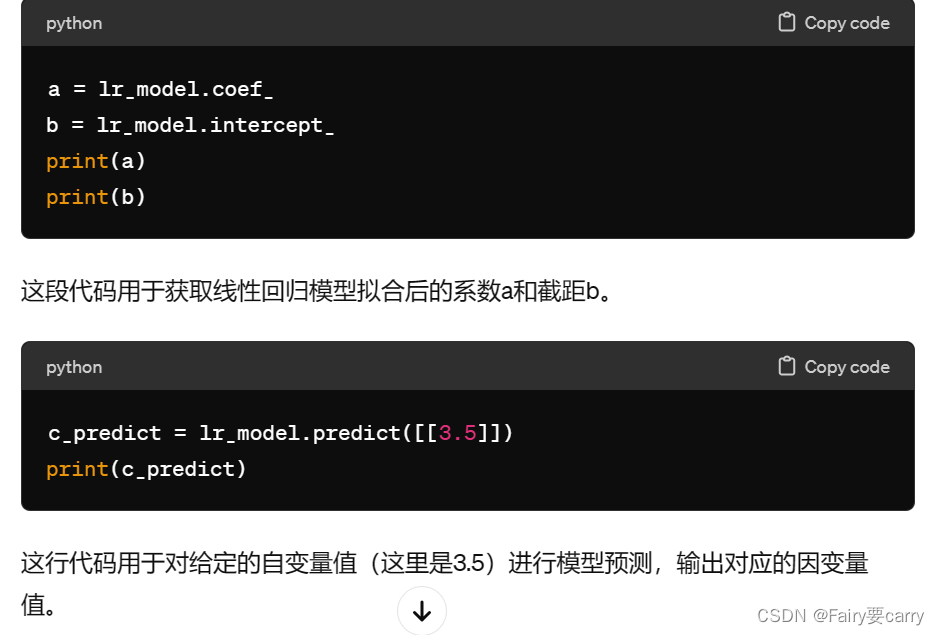
# 8.查看线性回归模型拟合后的系数a，b
a = lr_model.coef_
b = lr_model.intercept_
print(a)
print(b)
# 9.对X=3.5时进行模型预测y值
c_predict = lr_model.predict([[3.5]])
print(c_predict)
y_predict = lr_model.predict(X)
print(y_predict)
# 10.进行模型评估
MSE = mean_squared_error(y, y_predict)
R2 = r2_score(y, y_predict)
print(MSE)  # MSE接近0
print(R2)  # R2值接近1，拟合度很高
# 11.可视化y和y'
fig2 = plt.figure(figsize=(10, 10))
plt.scatter(y, y_predict)
plt.show()