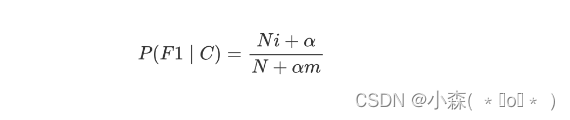ICLR 2022 Poster
Intro
部分离线强化学习的对价值函数采用的是最小化均方bellman误差。而其中误差源自单步的TD误差。TD误差中对target Q的计算需要选取一个max的动作,这就容易导致采取了OOD的数据。因此,IQL取消max,,通过一个期望回归算子实现利用数据集中数据去逼近最优的Q。
method
期望回归(Expectile Regression)
arg
min
m
τ
E
x
∼
X
[
L
2
τ
(
x
−
m
τ
)
]
,
\arg\min_{m_\tau}\mathbb{E}_{x\sim X}[L_2^\tau(x-m_\tau)],
argmτminEx∼X[L2τ(x−mτ)],
其中
L
2
τ
(
u
)
=
∣
τ
−
1
(
u
<
0
)
∣
u
2
.
L_2^\tau(u)=|\tau-\mathbb{1}(u<0)|u^2.
L2τ(u)=∣τ−1(u<0)∣u2. 函数如下所示

最右边的图可以看出,越大的
τ
\tau
τ使得预测值逼近上界。
IQL
IQL将上述的
L
2
τ
L_2^{\tau}
L2τ替换掉MSE来优化Q
L
(
θ
)
=
E
(
s
,
a
,
s
′
,
a
′
)
∼
D
[
L
2
τ
(
r
(
s
,
a
)
+
γ
Q
θ
^
(
s
′
,
a
′
)
−
Q
θ
(
s
,
a
)
)
]
.
L(\theta)=\mathbb{E}_{(s,a,s',a')\sim\mathcal{D}}[L_2^\tau(r(s,a)+\gamma Q_{\hat{\theta}}(s',a')-Q_\theta(s,a))].
L(θ)=E(s,a,s′,a′)∼D[L2τ(r(s,a)+γQθ^(s′,a′)−Qθ(s,a))].
然而上式存在一个问题。
Q
θ
^
Q_{\hat{\theta}}
Qθ^中采样的下一个动作具有一定的随机性,即使由较大的target Q也无法代表这是一个最优动作。因此这里来利用状态价值函数去并逼近这个Q:
L
V
(
ψ
)
=
E
(
s
,
a
)
∼
D
[
L
2
τ
(
Q
θ
^
(
s
,
a
)
−
V
ψ
(
s
)
)
]
.
L_V(\psi)=\mathbb{E}_{(s,a)\sim\mathcal{D}}[L_2^\tau(Q_{\hat{\theta}}(s,a)-V_\psi(s))].
LV(ψ)=E(s,a)∼D[L2τ(Qθ^(s,a)−Vψ(s))].
采用均值就有效增加鲁棒性。而得到 V 后将通过MSE来优化Q网络:
L
Q
(
θ
)
=
E
(
s
,
a
,
s
′
)
∼
D
[
(
r
(
s
,
a
)
+
γ
V
ψ
(
s
′
)
−
Q
θ
(
s
,
a
)
)
2
]
.
L_Q(\theta)=\mathbb{E}_{(s,a,s')\sim\mathcal{D}}[(r(s,a)+\gamma V_\psi(s')-Q_\theta(s,a))^2].
LQ(θ)=E(s,a,s′)∼D[(r(s,a)+γVψ(s′)−Qθ(s,a))2].
AWR
价值函数完成优化后便是优化策略。这里采用的是AWR方法
L
π
(
ϕ
)
=
E
(
s
,
a
)
∼
D
[
exp
(
β
(
Q
θ
^
(
s
,
a
)
−
V
ψ
(
s
)
)
)
log
π
ϕ
(
a
∣
s
)
]
L_\pi(\phi)=\mathbb{E}_{(s,a)\sim\mathcal{D}}[\exp(\beta(Q_{\hat{\theta}}(s,a)-V_\psi(s)))\log\pi_\phi(a|s)]
Lπ(ϕ)=E(s,a)∼D[exp(β(Qθ^(s,a)−Vψ(s)))logπϕ(a∣s)]