常用算法汇总

作者：指针不指南吗
专栏：算法篇

🐾算法思维逻辑🐾

文章目录

- 1.判断闰年
- 2.计算从某天到某天的天数
- 3.二分
- 4. 前缀和
- 5.差分
- 6.图论
- - 6.1dfs
  - 6.2走迷宫
- 7.最短路
- - 7.1dijkstra
  - 7.2foly
- 8.并查集
- 9.数论
- - 9.1gcd lcm
  - 9.2判断素数(质数)
  - 9.3分解质因子
  - 9.4快速幂
- 10.位运算
- - 10.1整数的奇偶性判断
  - 10.2有关 2 的幂的应用
  - 10.3 lowbit(x)返回x的最后一位1
  - 10.4二进制数中1的个数
  - 10.5求二进制位的某一位是几
  - 10.6交换两个整型变量的值
  - 10.7数组中x出现的次数
- 11.背包问题
- 12.动态规划
- 13.STL
- 14. 字符串
- 15.拿分

常用math函数
1.fabs（double x）对double变量取绝对值

2.pow（double r，double p）返回r的p次方 int 型同理

3.sqrt（double x）返回算术平方根

4.log（double x）返回以自然数为底的对数

如果想log a(b) = log(b) / log(a)

1.判断闰年

bool is_leap(int year)
{
	return year%400==0||(year%4!=0&&year%100!=0);
}

2.计算从某天到某天的天数

int end_year , end_month , end_day ;
int count_day(int year , int month , int day){
    int ans = 0 ;
    int mon[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
    while(1){
        if(end_year==year && end_month == month && end_day == day){
            break ;
        }
        day++;
		if(isLeaf(year) && month==2){
			if(day>mon[month]+1){
				month++;
				day=1;
			}
		}else{
			if(day>mon[month]){
				month++;
				day=1;
			}
		}
		if(month>12){
			month=1;
			year++;
		}
		ans++;
	}
	return ans;
}

3.二分

新的二分模板

判断条件：l+1!=r
求最左边，a[mid]>=k
求最右边，a[mid]<=k
操作都是mid=l\mid=r

判断等于号跟着谁
等于号跟着大于就是找的是左边小的
小于就是找的右边大的

acwing 791 数的范围

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int n,q;
int a[N];

int find(int k)
{
    int l=-1,r=n;

    while(l+1!=r)
    {
        int mid=(l+r)/2;
        if(a[mid]<=k) l=mid;
        else r=mid;
    }

    return l;
}


int find2(int k)
{
    int l=-1,r=n;

    while(l+1!=r)
    {
        int mid=(l+r)/2;
        if(a[mid]>=k) l=mid;
        else r=mid;
    }

    return r;
}

int main()
{
    cin>>n>>q;

    for(int i=0;i<n;i++)
        cin>>a[i];

    while(q--)
    {
        int k;
        cin>>k;

         int l=-1,r=n;

        while(l+1!=r)  //左边 小的
        {
            int mid=(l+r)/2;
            if(a[mid]>=k) r=mid;
            else l=mid;
        }

        if(k==a[r])
        {
            cout<<r<<' ';

            l=-1,r=n;

            while(l+1!=r)    //右边  大的
            {
                int mid=(l+r)/2;
                if(a[mid]<=k) l=mid;
                else r=mid;
            }
            cout<<l<<endl;
        }else{
            puts("-1 -1");
        }
    }


    return 0;
}

4. 前缀和

作用求区间和

scanf("%d",&a[i]);
s[i]+=a[i];

5.差分

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int a[N],b[N];

void insert(int l ,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        insert(i,i,a[i]);
    }
    
    while(m--)
    {
        int l,r,c;
        cin>>l>>r>>c;
        
        insert(l,r,c);
    }
    
    for(int i=1;i<=n;i++)
    {
        a[i]=a[i-1]+b[i];  //注意这里的公式
        cout<<a[i]<<' ';
    }
    
    return 0;
}

矩阵差分

原来的数组加上差分数组
原来的数组不能丢

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];



int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ ){
        	scanf("%d", &a[i][j]);
		}
    
    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        b[x1][y1] += c;
        b[x2 + 1][y1] -= c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }

    for (int i = 1; i <= n; i ++ ){
    	for (int j = 1; j <= m; j ++ ){
        	b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
        	printf("%d ", a[i][j]+b[i][j]);
		}
    	puts(" ");
	}
	
	return 0;
}

6.图论

6.1dfs

n皇后问题

 #include<bits/stdc++.h>
 using namespace std;
 
 int n;
 const int N=20;
 char q[N][N];  //存储棋盘
 bool cor[N],dg[2*N],udg[2*N];  //cor表示每一列，dg和udg表示正对角线和反对角线，来存储他们的是否被使用过的状态 
 
 void dfs(int u)  //放第 u 行的棋子 (深度优先遍历)
 {
     if(u==n) //如果放盘，则输出棋盘
     {
         for(int i=0;i<n;i++)
         {
             for(int j=0;j<n;j++)
                 cout<<q[i][j];
             cout<<endl;
         }
         
         cout<<endl;
         return ;  //重点！！ 递归到最深层，返回，千万别忘记
     }
     
     for(int i=0;i<n;i++)  //从第一列，开始遍历，是否放棋
     {
         if(!col[i]&&!dg[i+u]&&!udg[n-i+u])  //如果 列，对角线，没有被放过，则放皇后
         {
             q[u][i]='Q';  //放上
             col[i]=dg[i+u]=udg[n-i+u]=true;  //改变状态，dg[i+u]表示截距，每个对角线，都有自己独有的截距；反对角线的截距是负数，数组的下标，不能存放负数，所以加上 n这个偏移量
             dfs(u+1);  //放下一行的
             col[i]=dg[i+u]=udg[n-i+u]=false;  //恢复现场
             q[u][i]='.';
         }
     }
 }
 
 
 
 int main()
 {
     cin>>n;
     
     for(int i=0;i<n;i++)
         for(int j=0;j<n;j++)
             q[i][j]='.';  //初始化棋盘
     
     dfs(0);  //从第0行，开始放棋子
 
     return 0;
 }

6.2走迷宫

#include<bits/stdc++.h>
using namespace std;

typedef pair<int ,int> PII;  //定义 坐标

const int N=110;

int n,m;
int g[N][N];  //表示地图
int d[N][N];  //存的是某一点到源点的距离

int bfs()
{
    queue<PII> q;  //定义队列，里面存的表示我们将要走的哪一个点
    q.push({0,0});  //先把放进去，表示我们要走  起点
    
    memset(d,-1,sizeof d);  //初始化，把每个点到源点的距离初始化为  -1
    d[0][0]=0;  //源点到自己的距离为0
    
    int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};  //我们定义的四个方向 x,y 的移动，这样可以避免 4个判断语句，注意 dx，dy 要一一对应
    
    //从第一个开始位置开始遍历
    while(!q.empty())  //走到最后
    {
        auto t=q.front();  //把队列中的第一个元素取出来
        q.pop();  //对头元素出列
        
        for(int i=0;i<4;i++)
        {
            int x=t.first+dx[i],y=t.second+dy[i]; //扩展之后的坐标
            
            //x，y不能越界，可以走，没走过
            if(x>=0&&x<n&&y>=0&&y<m&&g[t.first][t.second]==0&&d[x][y]==-1)
            {
                d[x][y]=d[t.first][t.second]+1;  //距离+1
                q.push({x,y}); //把把满足条件地坐标插进去，下一次走它们
            }
        }
    }
    return d[n-1][m-1];  //返回最后一个即终点到源点地距离
}


int main()
{
    cin>>n>>m;
    
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin>>g[i][j];   //读入地图
            
    cout<<bfs()<<endl;
    
    return 0;
}

7.最短路

7.1dijkstra

#include<bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;

const int N=1.5*1e5+10;

int n,m;
int h[N],w[N],ne[N],e[N],idx;
int dist[N];
bool st[N];

void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;

    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1});

    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();

        int ver=t.second,distance=t.first;

        if(st[ver]) continue;

        st[ver]=1;

        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>distance+w[i])
            {
                dist[j]=distance+w[i];
                heap.push({dist[j],j});
            }
        }
    }

    if(dist[n]==0x3f3f3f3f)  return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d",&n,&m);

    memset(h,-1,sizeof h);

    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }

    int t=dijkstra();

    cout<<t;

    return 0;
}

7.2foly

#include<bits/stdc++.h>
using namespace std;

const int N=210;
const int INF=1e9;

int n,m,k;
int g[N][N];

void floyd()
{
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}

int main()
{
    scanf("%d%d%d",&n,&m,&k);

    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j) g[i][j]=0;
            else g[i][j]=INF;

    int a,b,c;    
    while(m--)
    {
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=min(c,g[a][b]);
    }

    floyd();

    while(k--)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        if(g[x][y]>=INF/2)  
            puts("impossible");
        else cout<<g[x][y]<<endl;
    }

    return 0;
}

8.并查集

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int n,m;
int p[N];

int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
        p[i]=i;

    int a,b;
    char op[2];

    while(m--)
    {
        cin>>op>>a>>b;

        if(op[0]=='M')
        {
            p[find(a)]=p[find(b)];
        }
        else
        {
            if(find(a)==find(b))
                puts("Yes");
            else
                puts("No");
        }
    }

    return 0;
}

9.数论

9.1gcd lcm

//最大公约数
int gcd(int x,int y)
{
	return y?gcd(y,x%y):x;
}

//最小公倍数
int lcm(int x,int y)
{
	return x*y/gcd(x,y);
}

9.2判断素数(质数)

bool isprime(int n)
{
	if(n<=3)   //特判几个较小的数
		return n>1;
		
	if(n%6!=1&&n%6!=5)  //不在6的倍数的两侧，一定不是素数
		return 0;
		
	for(int i=5;i<=sqrt(n);i+=6)  //判断在6的倍数的两侧的数，是不是素数
		if(n%i==0||n%(i+2)==0)
			return 0;
			
	return 1;
}

9.3分解质因子

题目

链接： AcWing 867. 分解质因数- AcWing

给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式

对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围

1≤n≤100,
2≤ai≤2× $10^9$

输入样例：
2
6
8
输出样例：
2 1
3 1

2 3

分析

x 的质因子最多只包含一个大于根号x 的质数。如果有两个，这两个因子的乘积就会大于 x，矛盾。
i 从 2 遍历到根号x。用 x / i，如果余数为 0，则 i 是一个质因子。
s 表示质因子 i 的指数，x /= i 为 0，则 s++， x = x / i 。
最后检查是否有大于根号x 的质因子，如果有，输出。

代码实现

#include<bits/stdc++.h>
using namespace std;

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )//i <= x / i:防止越界，速度大于 i < sqrt(x)
        if (x % i == 0)//i为底数
        {
            int s = 0;//s为指数
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;//输出
        }
    if (x > 1) cout << x << ' ' << 1 << endl;//如果x还有剩余，单独处理
    cout << endl;
}

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        divide(x);
    }

    return 0;
}

9.4快速幂

给你三个整数 a,b,p，求 $a^ b mod p$ 。
题目链接：P1226 【模板】快速幂 | 取余运算

取平方思路

参考文章：https://oi-wiki.org/math/binary-exponentiation/

先看这个式子 $a^{2b}=a^2*a^b$ ,我们发现取平方可以缩短计算次数，我们可以按照 二进制 来表示幂。那我们来看看幂和二进制之间的关系。

举个例子讲解：例如： $3^{13}=3^{(1101)_2}=3^8*3^4*3^1$

是不是发现，这里面只有二进制位是1的才乘到里面，是0的跳过，所以我们只需要用10进制转2进制的方法（不断÷2的余数，直到商为0），即可得到幂数对应的二进制数。**如果某一个二进制位是1，那就将对应的数乘到结果里面，并且底数也翻倍；如果是0，则底数也翻倍。**可看下面的推导过程，这个地方有点绕，跟着过一遍就懂了。

取模定理

(a * b) % p = (a % p * b % p) % p （3）

乘积的取模等于各个因子取模相乘然后再取模；

取模的运算不会干涉乘法运算，因此我们只需要在计算的过程中取模即可。

快速幂代码实现

long long binpow(long long a, long long b) 
{
    long long res = 1;
    while (b > 0) 
    {
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
  	}
  	return res;
}

快速幂取模代码实现

long long binpow(long long a, long long b, long long m) 
{
	a %= m;
    long long res = 1;
    while (b > 0) 
    {
        if (b & 1) res = res * a % m;
        a = a * a % m;
        b >>= 1;
  	}
  	return res;
}

10.位运算

位运算就是直接对整数在内存中的二进制位进行操作，由于计算机内部就是以二进制来存储数据，位运算是相当快的。

基本的位运算共 6种，分别为按位与、按位或、按位异或、按位取反、左移和右移。

位运算一般有三种作用：

高效地进行某些运算，代替其它低效的方式。
表示集合。（常用于状压DP ）
题目本来就要求进行位运算。

位运算符

含义	符号	简述
按位与	a & b	同一得 1
按位或	a \| b	有一得 1
按位异或	a ^ b	相同得 0
按位取反	~a	取反
左移	a << b	向左移动，低位补零，高位舍弃
带符号右移	a >> b	向右移动，高位补原有高位，低位舍弃

复合赋值位运算符

和 += , -= 等运算符类似，位运算也有复合赋值运算符： &= , |= , ^= , <<= , >>= 。（取反是单目运算，所以没有）
数组初始化

memset(f,0x3f,sizeof(f))

位移运算符

左移运算符 <<
二进制 ： 1 -> 10 -> 100 -> 1000
十进制 ： 1 -> 2  -> 4   -> 8
综上所述：1 << n  ==  2^n
右移运算符 >>
二进制 ： 1000 -> 100 -> 10 -> 1
十进制 :  8    -> 4   -> 2  -> 1
综上所述: n >> x  == n / (2^x)

运算符优先级

~的优先级最高，其次是<<、>>，再次是＆，然后是^，优先级最低的是|。

位运算的优先级低于算术运算符（除了取反），而按位与、按位或及异或低于比较运算符（详见运算页面），所以使用时需多加注意，在必要时添加括号。

位运算应用

10.1整数的奇偶性判断

朴素做法

if(a%2==1)
    //为奇数
else
    //为偶数

按位与 -> 二进制的末位为0表示偶数，最末位为1表示奇数
```
if(a & 1 != 1)
    //为奇数
else
    //为偶数
```

10.2有关 2 的幂的应用

将一个数乘（除） 2 的非负整数次幂

// 计算 n*(2^m)
int mulPowerOfTwo(int n, int m)   
{
  return n << m;
}

// 计算 n/(2^m)
int divPowerOfTwo(int n, int m)   
{
  return n >> m;
}

判断一个数是否是2的幂次方，若是，并判断出来是多少次方

题目链接：力扣 231. 2的幂

将2的幂次方写成二进制形式后，很容易就会发现有一个特点：二进制中只有一个1，并且1后面跟了n个0；因此问题可以转化为判断1后面是否跟了n个0就可以了

如果将这个数减去1后会发现，仅有的那个1会变为0，而原来的那n个0会变为1；因此将原来的数与去减去1后的数字进行与运算后会发现为零。
   最快速的方法：

  (number & number - 1) == 0

  原因：因为2的N次方换算是二进制为10……0这样的形式(0除外)。按位与上自己-1的位数，这们得到结果为0。例如，8的二进制为1000；8-1=7，7的二进制为111。两者相与的结果为0。计算如下：
     1000
   & 0111
   -------
     0000

代码实现如下：

#include<bits/stdc++.h>
using namespace std;
 
//判断一个数是2的多少次方
int log2(int value)   
{
	int x=0;
	while(value>1)
	{
		value>>=1;
		x++;
	}
	return x;
}
 
int main()
{
	int num;
	scanf("%d",&num);
    
    //使用与运算判断一个数是否是2的幂次方
	if(num&(num-1))     
		printf("%d不是2的幂次方！\n",num);
	else
		printf("%d是2的%d次方！\n",num,log2(num));
    
	return 0;
}

10.3 lowbit(x)返回x的最后一位1

lowbit(x)：返回x的最后一位1，即一个二进制最低位的1与后边的0组成的数。

x = 1010 lowbit(x) = 10

x= 101000 lowbit(x) = 1000

实现原理：x & -x = x & (~x + 1)，负数的补码：原码取反加一（利用了负整数的补码特性）

10.4二进制数中1的个数

题目链接：力扣 191.位1的个数

朴素做法 -> 使用移位操作，判末位是否为1；移位的次数为32

int BitCount(unsigned int n)
{
    unsigned int c =0 ; // 计数器
    while (n >0)
    {
        if((n &1) ==1) // 当前位是1
            ++c ; // 计数器加1
        n >>=1 ; // 移位
    }
    return c ;
}

快速做法 -> 迭代n=n&(n-1)，消除最右边的1，计数

int BitCount2(unsigned int n)
{
    unsigned int c =0 ;
    for (c =0; n; ++c)
    {
        n &= (n -1) ; // 清除最低位的1
    }
    return c ;
}

10.5求二进制位的某一位是几

n 的二进制中第 k 位数字

先把第k为移到最后一位 n>>k

看个位是几 x&1

把上面两步综合即 n>>k&1

应用：输出n=10的二进制

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n=10;
    
    for(int k=3;k>=0;k--) //从0位开始的（右到左）
        cout<<(n>>k&1);
    
    return 0;
}

10.6交换两个整型变量的值

异或的性质：

1.交换律：可任意交换运算因子的位置，结果不变；

如：a ^ b ^ c = b ^ a ^ c;

2.结合律：即(a ^ b) ^ c == a ^ ( b ^ c) ;

3.对于任何数x, 都有x ^ x = 0, x ^ 0 = x,同自己求异或为0，同0求异或为自己

4.自反性：A ^ B ^ B = A ^ 0 = A, 连续和同一个因子做异或运算，最终结果为自己

例题：int A = 10, int B = 20, 在不引入第3个变量的情况下，交换两个变量的值。

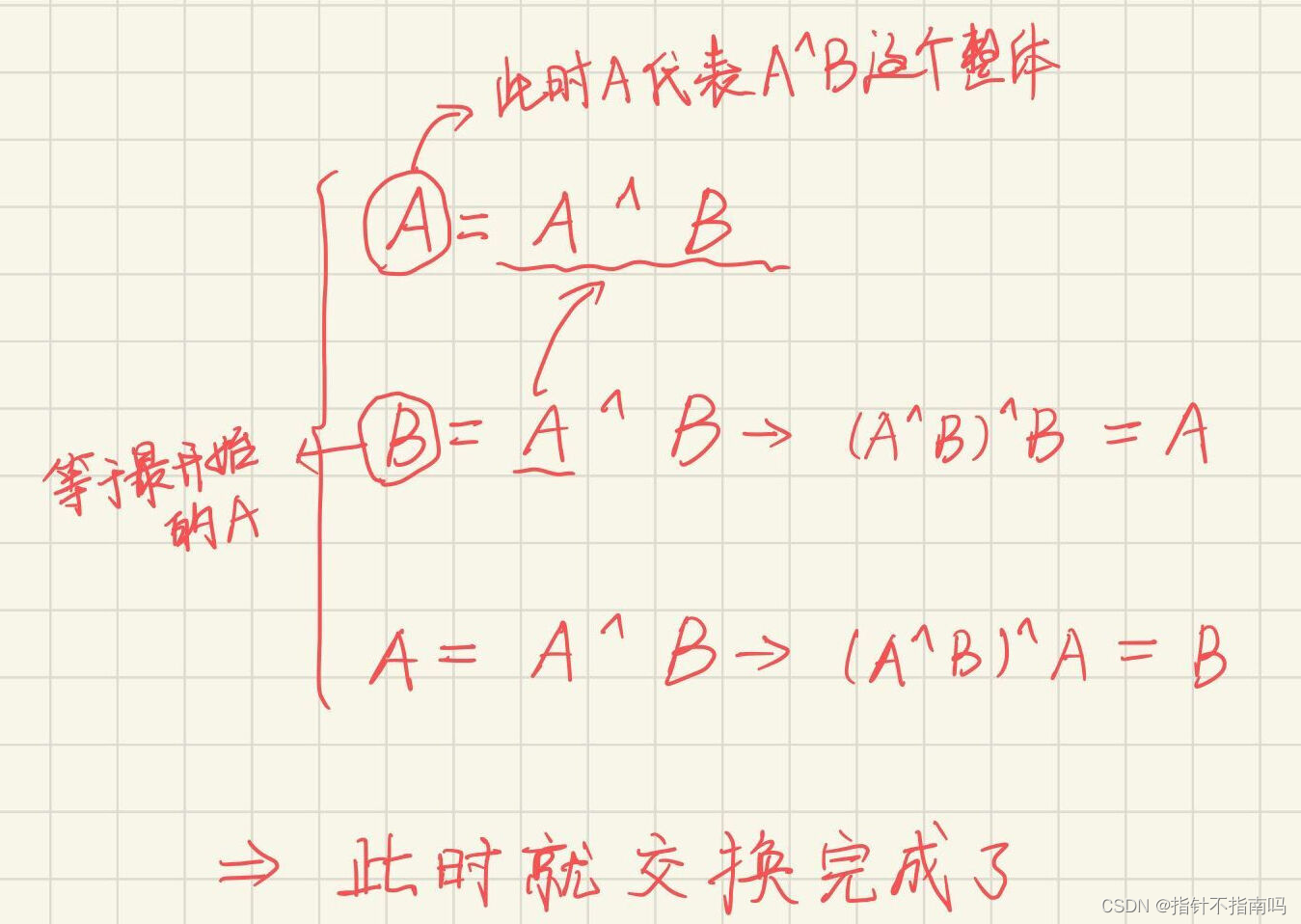
异或法——代码实现

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int A = 10;
    int B = 20;
    printf("交换前A = %d B = %d\n", A, B);
    A = A ^ B;
    B = A ^ B;
    A = A ^ B;
    printf("交换后A = %d B = %d\n", A, B);
    return 0;	
}

10.7数组中x出现的次数

应用一：数组中，只有一个数出现一次，剩下都出现两次，找出出现一次的数
题目链接：力扣 136.只出现一次的数字 |

因为只有一个数恰好出现一个，剩下的都出现过两次，所以只要将所有的数异或起来，就可以得到唯一的那个数，因为相同的数出现的两次，异或两次等价于没有任何操作。

代码实现

int singleNumber(int nums[]) 
{
    int result = 0, n = sizeof(nums)/sizeof(nums[0]);

    for (int i = 0; i < n; i++)
    {
        result ^= nums[i];
    }
    return result;
}

应用二：数组中，只有一个数出现一次，剩下都出现三次，找出出现一次的数

题目链接：力扣 137.只出现一次的数字||

为了方便叙述，我们称「只出现了一次的元素」为「答案」。

由于数组中的元素都在 int（即 32 位整数）范围内，因此我们可以依次计算答案的每一个二进制位是 0还是1。具体地，考虑答案的第 i 个二进制位（i 从0开始编号），他可能为0或者1。对于数组中非答案的元素，每个元素都出现了3次，3次对应第i个二进制位和的3个0或者3个1，无论哪一种情况，他的结果相加（0或者3）都是3的倍数，答案的第 i 个二进制位就是数组中所有元素的第 i 个二进制位之和除以 3 的余数。

这样一来，对于数组中的每一个元素 x，我们使用位运算（x>>i）&1 得到 x 的第 i 个二进制位，并将它们相加再对 3 取余，得到的结果一定为 0 或 1，即为答案的第 i 个二进制位。

代码实现

int singleNumber(vector<int>& nums) 
{
    int ans = 0;
    for (int i = 0; i < 32; ++i) {
        int total = 0;
        for (int num: nums) {
            total += ((num >> i) & 1);
        }
        if (total % 3) {
            ans |= (1 << i);
        }
    }
    return ans;
}

针对上面进行拓展，如果是数组中，只有一个数出现一次，剩下都出现 k 次，找出出现一次的数呢

total % k  //将3改为 k ，对 k 进行取模即可

应用三：如何找数组中唯一成对的那个数

1-10这10个数放在含有11个元素的数组中，只有唯一一个元素重复，其他均只出现一次，要求每个数组元素只能够被访问一次，请设计一个算法，将它找出来。

位运算中异或 ^ 的特点，A^A=0 A^0=A ,也就是说，两个相同的数字进行异或结果为0，可以用来消除重复。可惜，题目要求寻找重复的值，所以，我们对这1001个数字加上（1 ~ 1000）这1000个数字，这样1~1000所有的数字出现了2次，可以消除，而那个重复的数字由于加了一次，变成了3次，A ^ A ^ A =A。从而得出那个重复的A。

代码实现

int findDouble(int T[])
{
    int res=0; //定义一个返回结果，初始值为0，因为A^0=A
    
    //先对T数组进行异或
    for(int i=0;i<T.length;i++)
    {
        res^=T[i];
    }
    
    //在与1~1000异或
    for(int i=1;i<=1000;i++)
    {
        res^=i;
    }
    return res;
}