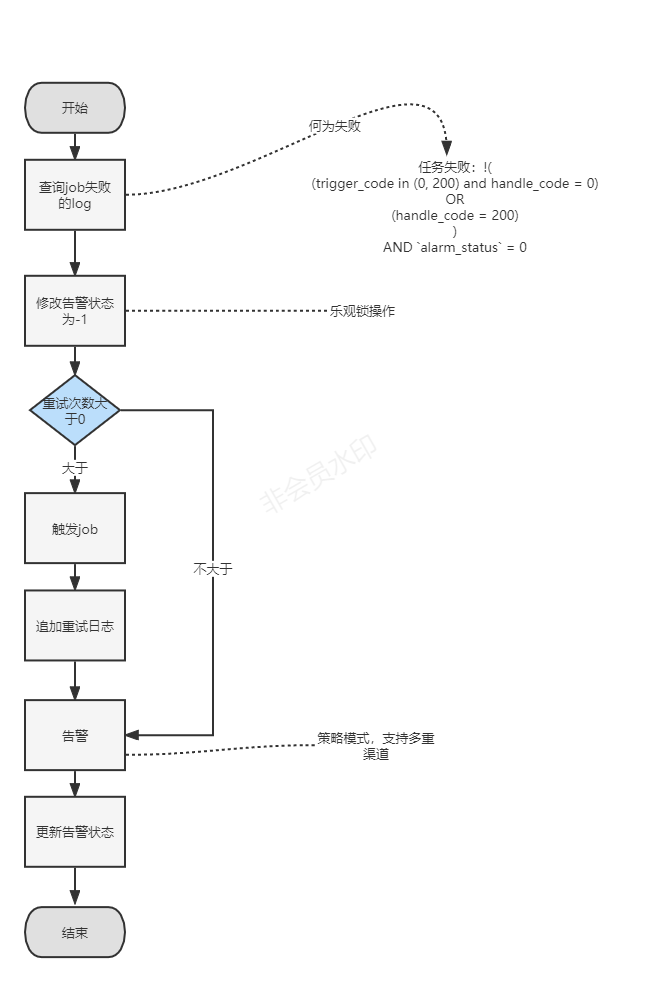
目录
- 1.码间干扰
- 2.无码间干扰条件
- 2.1 时域条件
- 2.2 频域条件
- 3.满足无码间干扰条件的滤波器
- 3.1 理想低通滤波器
- 3.2 余弦滚降滤波器
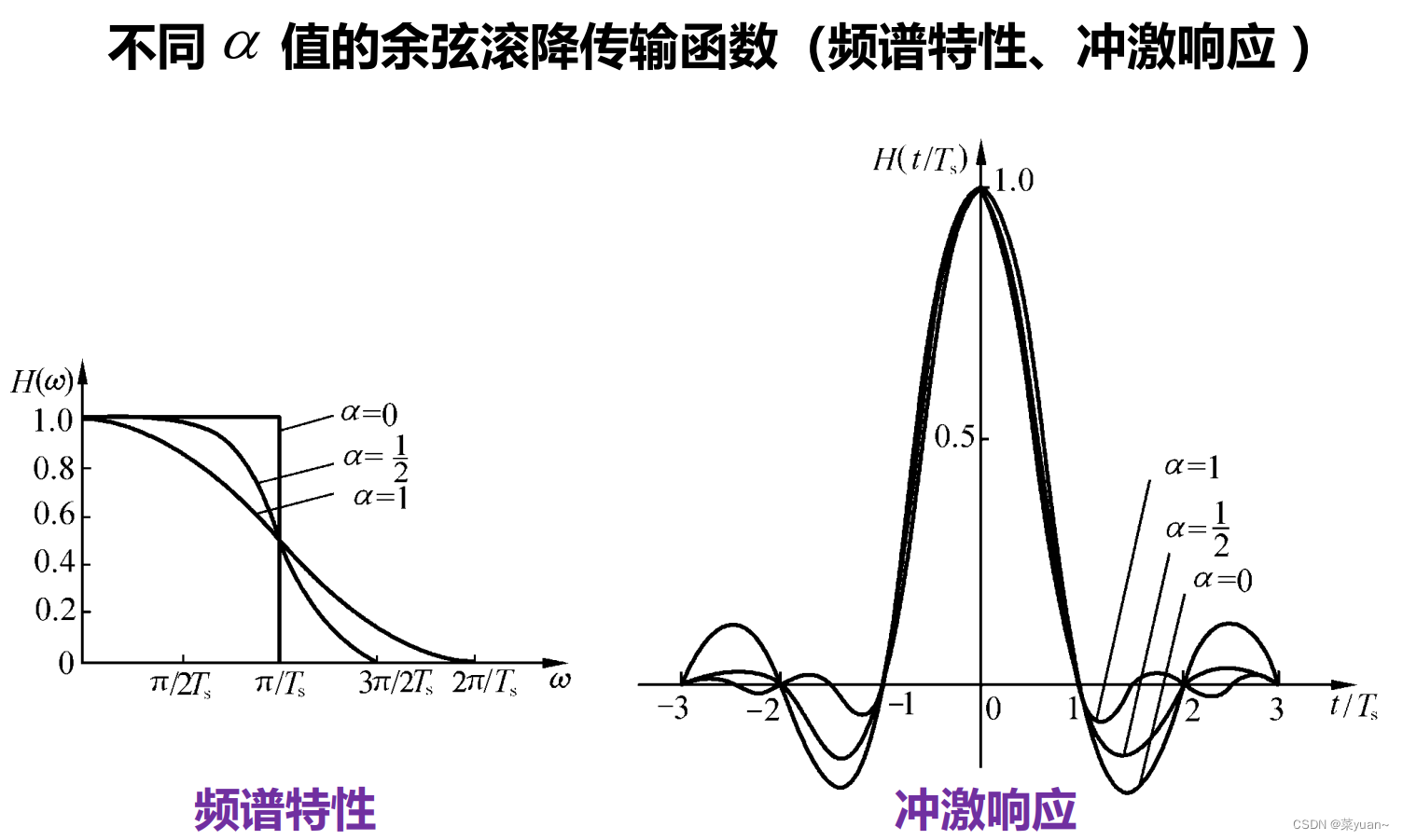
- 4.不同滚降系数的余弦滚降滤波器时频域图
- 4.1 代码
- 4.2 结果图
- 5.理想低通滤波器和升余弦滚降滤波器(α=1)对比
1.码间干扰
如下图所示,码间干扰的产生是接收端在当前采样时刻,除了接收到当前的码元,还接收到其他码元在当前采样时刻的叠加值之和,该叠加值之和即码间干扰。
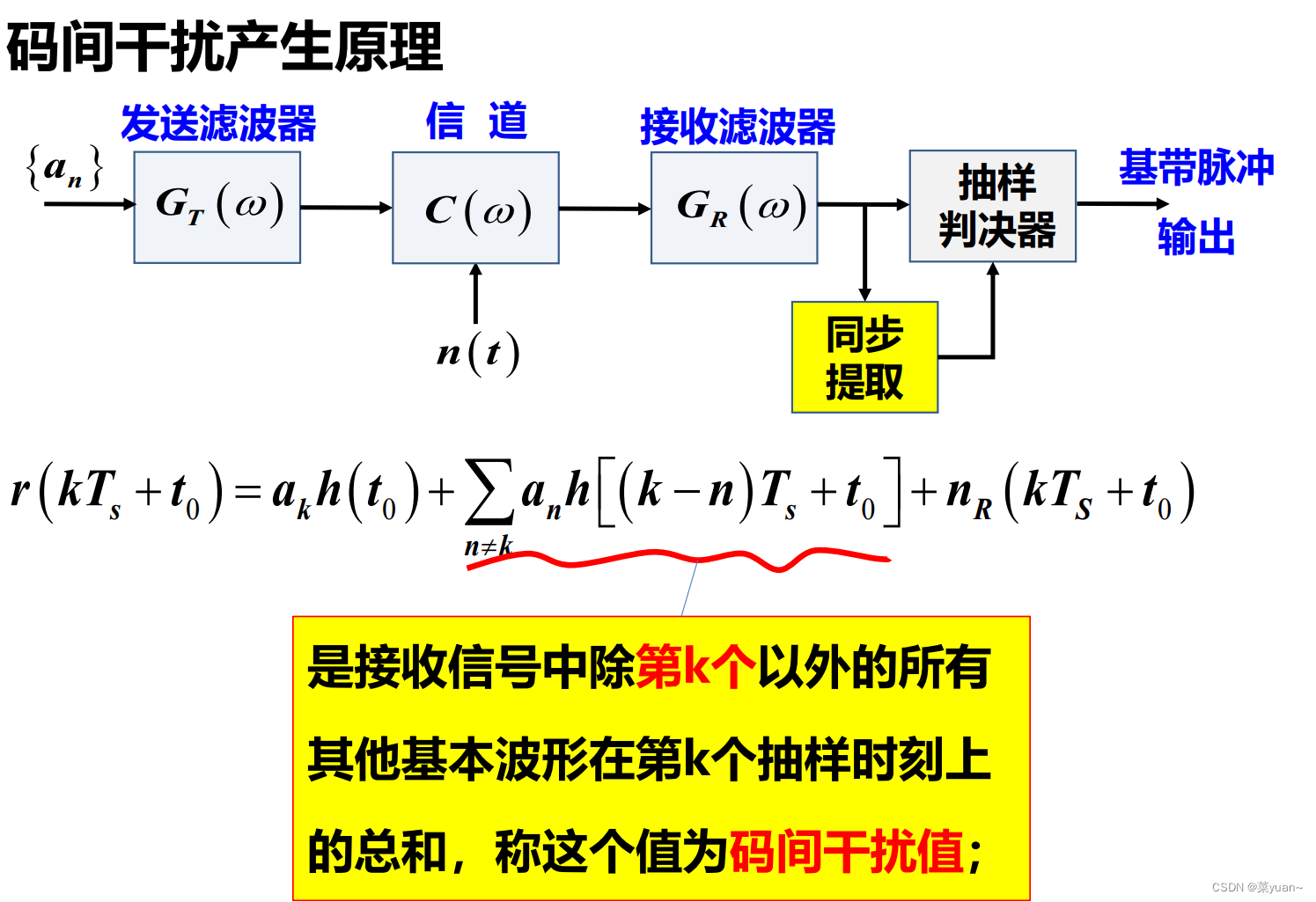
2.无码间干扰条件
2.1 时域条件
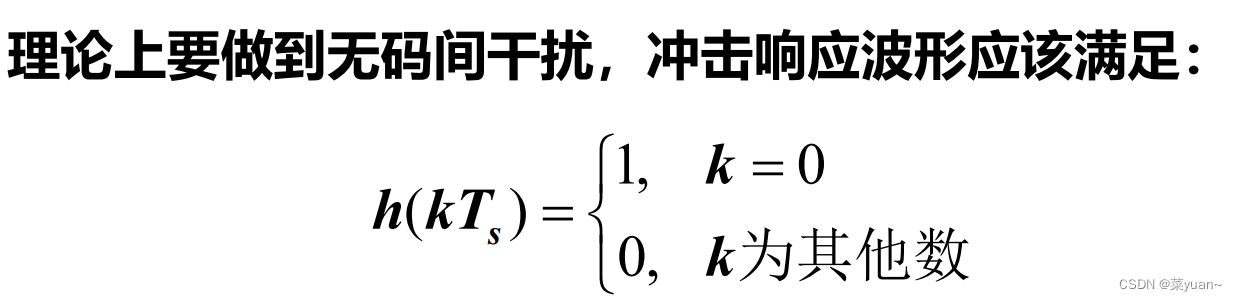
2.2 频域条件

3.满足无码间干扰条件的滤波器
3.1 理想低通滤波器

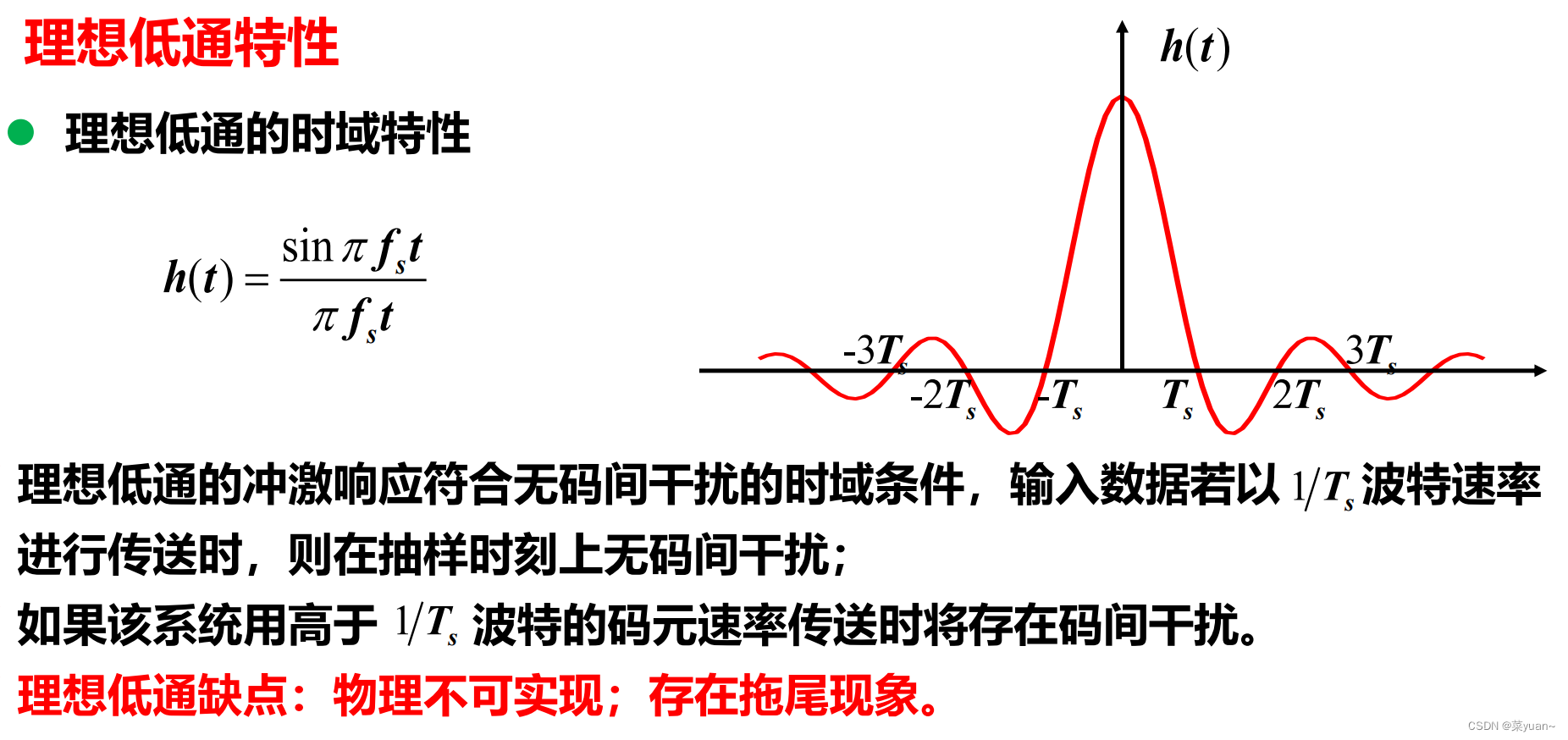
3.2 余弦滚降滤波器
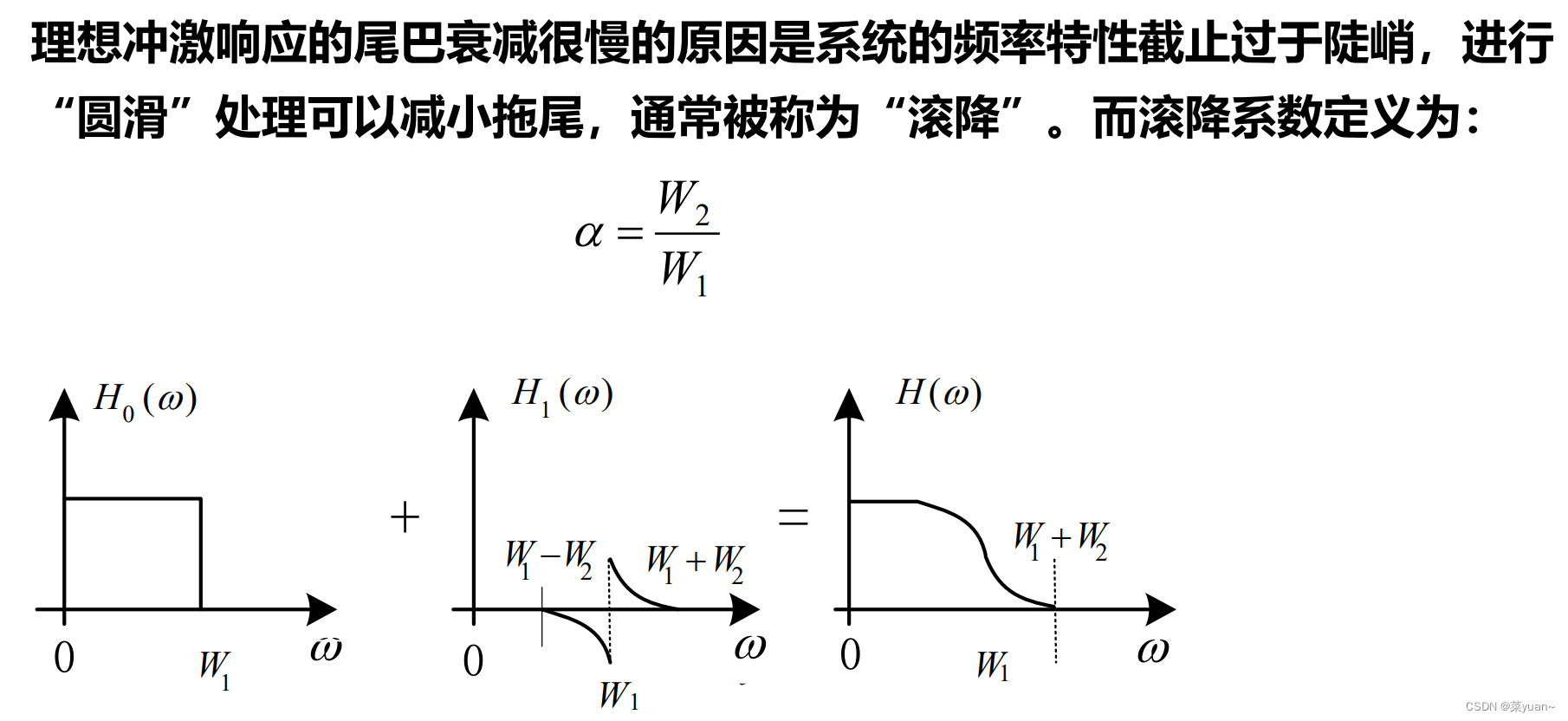

4.不同滚降系数的余弦滚降滤波器时频域图
4.1 代码
clear all % 清除所有变量
Ts=0.001; % 码元宽度
N=10; % 单个码元采样点数
dt=Ts/N; % 采样间隔
fs=1/dt; % 采样频率
t=-10*Ts:dt:10*Ts; % 10个码元的持续时间
df=1.0/(20.0*Ts); % 频谱分辨率
f=-fs/2:df:fs/2; % 频谱范围-fs/2到fs/2
alpha=[0,0.5,1]; % 滚降系数
% 余弦滚降的传输函数
for n=1:length(alpha)
for k=1:length(f)
if abs(f(k))>0.5*(1+alpha(n))/Ts
Xf(n,k)=0;
elseif abs(f(k))<0.5*(1-alpha(n))/Ts
Xf(n,k)=Ts;
else
Xf(n,k)=0.5*Ts*(1+cos(pi*Ts/(alpha(n)+eps)*(abs(f(k))-0.5*(1-alpha(n))/Ts)));
end
end
xt(n,:)=sinc(t/Ts).*(cos(alpha(n)*pi*t/Ts))./(1-4*alpha(n)^2*t.^2/Ts^2+eps);
end
figure(1); % 绘制时频域图
subplot(211) % 将窗口分割成2*1的,当前是第1个子图
plot(f,Xf(1,:),'g','LineWidth',2); % 绘制滚降系数为0的余弦滚降频谱,线宽为2,绿色
hold on; % 保留之前的不被刷新,继续在同一个图中绘制
plot(f,Xf(2,:),'b','LineWidth',2); % 绘制滚降系数为0.5的余弦滚降频谱,线宽为2,蓝色
plot(f,Xf(3,:),'r','LineWidth',2); % 绘制滚降系数为1的余弦滚降频谱,线宽为2,红色
axis([-fs/4 fs/4 -inf inf]); % 坐标轴范围设置
xlabel('f/Ts'); % x轴标签
ylabel('幅度'); % y轴标签
title('余弦滚降频谱'); % 标题
subplot(2,1,2) % 将窗口分割成2*1的,当前是第2个子图
plot(t,xt(1,:),'g','LineWidth',1); % 绘制滚降系数为0的余弦滚降时域图,线宽为1,绿色
hold on; % 保留之前的不被刷新,继续在同一个图中绘制
plot(t,xt(2,:),'b','LineWidth',1); % 绘制滚降系数为0.5的余弦滚降时域图,线宽为1,蓝色
plot(t,xt(3,:),'r','LineWidth',1); % 绘制滚降系数为1的余弦滚降时域图,线宽为1,红色
xlabel('t'); % x轴标签
ylabel('幅度'); % y轴标签
title('余弦滚降波形'); % 标题
4.2 结果图

5.理想低通滤波器和升余弦滚降滤波器(α=1)对比
理想低通滤波器的频带利用率高,但是物理不可实现;
升余弦滚降滤波器可以实现,但是频带利用率低。




![误删照片音视频文件不要担心 几种方法解救慌乱的你 别再病急乱投医啦 [附软件]](https://img-blog.csdnimg.cn/71564d2e102942a5b7c9368343f666db.png)