练习题（2024/5/7）

1验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左
子树
只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

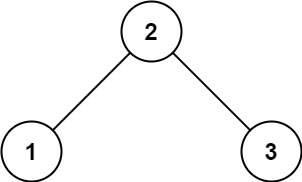
输入：root = [2,1,3]
输出：true

示例 2：

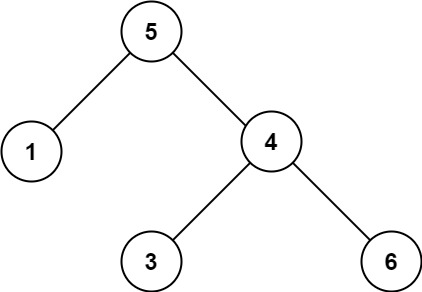
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

思路1：

中序遍历下，输出的二叉搜索树节点的数值是有序序列。

有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了 我们把二叉树转变为数组来判断，是最直观的

通过中序遍历将二叉搜索树转换为有序数组，然后检查该数组是否严格递增。中序遍历保证了二叉搜索树的节点按照从小到大的顺序被访问，因此如果数组中存在相邻元素相等或逆序，则说明不满足二叉搜索树的性质

代码：

class Solution {
private:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
public:
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 清空数组
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            // 判断是否是二叉搜索树的条件
            if (vec[i] <= vec[i - 1]) return false;
        }
        return true;
    }
};

思路2：

不用转变成数组，可以在递归遍历的过程中直接判断是否有序。

利用递归来检查二叉搜索树的有效性。首先，通过递归遍历左子树，确保左子树是一个有效的二叉搜索树；然后，检查当前节点是否大于前一个节点（中序遍历时前一个节点的值），如果不是则返回 false；最后，递归遍历右子树，确保右子树也是一个有效的二叉搜索树。整体思路是基于二叉搜索树的性质，即左子树的所有节点小于根节点，右子树的所有节点大于根节点。

代码：

class Solution {
public:
    TreeNode* pre = NULL; // 用来记录前一个节点

    // 检查是否为有效的二叉搜索树
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        bool left = isValidBST(root->left); // 检查左子树

        // 如果前一个节点不为空且大于等于当前节点的值，则不是二叉搜索树
        if (pre != NULL && pre->val >= root->val) return false;
        pre = root; // 记录前一个节点

        bool right = isValidBST(root->right); // 检查右子树
        return left && right;
    }
};

思路3：

迭代法解题思路是基于中序遍历二叉搜索树的特性。首先，我们使用一个栈来模拟中序遍历过程。从根节点开始，将所有左子节点依次入栈，直到最左的叶子节点。然后，开始出栈操作，每次出栈一个节点，判断其值是否大于前一个访问的节点值（如果有的话）。如果不是，则说明不满足二叉搜索树的定义，直接返回 false。如果满足，则更新前一个访问的节点，并将当前节点的右子节点入栈。这样，通过迭代遍历整个树，如果全部节点都满足二叉搜索树的定义，则返回 true

代码：

class Solution {
public:
    // 判断是否为有效的二叉搜索树
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st; // 创建一个栈
        TreeNode* cur = root; // 当前节点指针
        TreeNode* pre = NULL; // 记录前一个节点
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) {
                st.push(cur);
                cur = cur->left; // 遍历左子树
            } else {
                cur = st.top(); // 中序遍历当前节点
                st.pop();
                // 如果当前节点值小于等于前一个节点值，则不是二叉搜索树
                if (pre != NULL && cur->val <= pre->val)
                    return false;
                pre = cur; // 保存前一个访问的结点

                cur = cur->right; // 遍历右子树
            }
        }
        return true;
    }
};

2二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

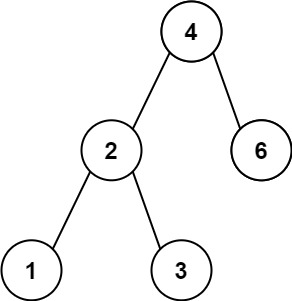
输入：root = [4,2,6,1,3]
输出：1

示例 2：

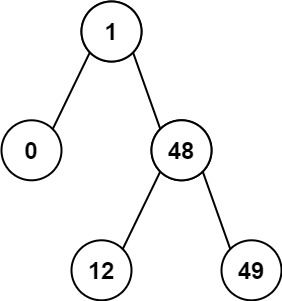
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

思路：

首先，通过中序遍历二叉搜索树，将节点值按照从小到大的顺序存储在一个数组中。这样，得到的数组就是一个有序数组。然后，遍历这个有序数组，计算相邻两个节点值的差值，找出其中的最小值，即为任意两节点的最小差值。整体思路是利用中序遍历得到有序数组的特性，然后在有序数组上进行差值计算，从而求得最小差值。

代码：

class Solution {
private:
    vector<int> vec; // 存储中序遍历后的有序数组
    // 中序遍历二叉树，将节点值存入有序数组中
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }

public:
    // 计算二叉搜索树任意两节点的最小差值
    int getMinimumDifference(TreeNode* root) {
        vec.clear(); // 清空有序数组
        traversal(root); // 中序遍历，得到有序数组
        if (vec.size() < 2) return 0; // 如果节点数量小于2，直接返回0
        int result = INT_MAX; // 初始化结果为最大值
        // 遍历有序数组，计算相邻节点的差值，找出最小的差值
        for (int i = 1; i < vec.size(); i++) {
            result = min(result, vec[i] - vec[i-1]);
        }
        return result; // 返回最小差值
    }
};

思路2：

在中序遍历的过程中，每次比较当前节点和前一个节点的差值，更新最小差值的结果。首先初始化一个最大值作为结果变量，一个空指针pre用于保存前一个节点的指针。然后进行中序遍历，遍历左子树，比较当前节点和前一个节点的值，更新结果。每次遍历完成后，更新pre指针，继续遍历右子树。最终返回计算得到的最小差值。整体思路是通过中序遍历一次得到有序数组，但是在计算最小差值的过程中，不需要保存整个数组，只需要保存前一个节点指针进行比较即可。

代码：

class Solution{
private:
      int result=INT_MAX; // 存储节点值最小差值的结果
      TreeNode* pre=NULL; // 前一个访问的节点指针，用于计算相邻节点的差值
      void traversal(TreeNode *cur){
        if(cur == nullptr) return; // 递归终止条件
        traversal(cur->left); // 左子树递归遍历
        if(pre != nullptr){
            result = min(result, cur->val-pre->val); // 更新最小差值
        }
        pre = cur; // 更新前一个访问的节点
        traversal(cur->right); // 右子树递归遍历
      }
public:
     int getMinimumDifference(TreeNode* root){
        traversal(root); // 递归遍历整个二叉搜索树
        return result; // 返回最小差值结果
   }
}; // 加中文注释

3二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

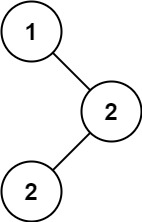
输入：root = [1,null,2,2]
输出：[2]

示例 2：

输入：root = [0]
输出：[0]

提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

思路：

既然是搜索树，它中序遍历就是有序的。

在中序遍历的过程中，通过比较当前节点和前一个节点的值来统计当前节点出现的次数，同时更新最大出现次数和众数结果。首先初始化计数变量count和最大出现次数变量maxCount，以及存储结果的vector。然后进行中序遍历，遍历左子树，比较当前节点和前一个节点的值，更新计数。如果当前节点的值与前一个节点相同，则增加计数；否则重新设置计数为1。更新前一个访问的节点指针pre，并根据计数更新结果和最大出现次数。最终返回存储众数结果的vector。整体思路是在中序遍历的过程中，通过比较当前节点和前一个节点的值来统计出现次数，同时更新最大出现次数和众数结果，最终返回找到的众数值。

代码：

class Solution{
private:
   int count=0; // 统计当前节点出现的次数
   int maxCount =0; // 统计最大出现次数
   vector<int> result; // 存储众数的结果
   TreeNode* pre =nullptr; // 前一个访问的节点指针
   void searchBST(TreeNode* cur){
    if(cur ==nullptr) return; // 递归终止条件
    searchBST(cur->left); // 左子树递归遍历
    if(pre ==nullptr) {
        count=1; // 初始情况下设置当前节点出现次数为1
    } else if(pre->val== cur->val){
        count++; // 当前节点值与前一个节点相同，增加计数
    } else {
        count=1; // 当前节点值与前一个节点不同，重新设置计数为1
    } 
    pre =cur; // 更新前一个访问的节点
    if(count ==maxCount){
        result.push_back(cur->val); // 结果中添加当前众数
    }
    if(count>maxCount){
        maxCount=count; // 更新最大出现次数
        result.clear();
        result.push_back(cur->val); // 清空结果，加入当前节点值
    }
    searchBST(cur->right); // 右子树递归遍历
    return;
   }
    
public:
     vector<int> findMode(TreeNode* root){
        count=0; // 初始化变量
        maxCount =0;
        pre=nullptr;
        result.clear();
        searchBST(root); // 开始搜索二叉搜索树
        return result; // 返回众数结果
     }
};

4查找拥有有效邮箱的用户

表: Users

+---------------+---------+
| Column Name   | Type    |
+---------------+---------+
| user_id       | int     |
| name          | varchar |
| mail          | varchar |
+---------------+---------+
user_id 是该表的主键（具有唯一值的列）。
该表包含了网站已注册用户的信息。有一些电子邮件是无效的。

编写一个解决方案，以查找具有有效电子邮件的用户。

一个有效的电子邮件具有前缀名称和域，其中：

前缀名称是一个字符串，可以包含字母（大写或小写），数字，下划线 '_' ，点 '.' 和/或破折号 '-' 。前缀名称必须以字母开头。
域为 '@leetcode.com' 。

以任何顺序返回结果表。

结果的格式如以下示例所示：

示例 1：

输入：
Users 表:
+---------+-----------+-------------------------+
| user_id | name      | mail                    |
+---------+-----------+-------------------------+
| 1       | Winston   | winston@leetcode.com    |
| 2       | Jonathan  | jonathanisgreat         |
| 3       | Annabelle | bella-@leetcode.com     |
| 4       | Sally     | sally.come@leetcode.com |
| 5       | Marwan    | quarz#2020@leetcode.com |
| 6       | David     | david69@gmail.com       |
| 7       | Shapiro   | .shapo@leetcode.com     |
+---------+-----------+-------------------------+
输出：
+---------+-----------+-------------------------+
| user_id | name      | mail                    |
+---------+-----------+-------------------------+
| 1       | Winston   | winston@leetcode.com    |
| 3       | Annabelle | bella-@leetcode.com     |
| 4       | Sally     | sally.come@leetcode.com |
+---------+-----------+-------------------------+
解释：
用户 2 的电子邮件没有域。 
用户 5 的电子邮件带有不允许的 '#' 符号。
用户 6 的电子邮件没有 leetcode 域。 
用户 7 的电子邮件以点开头

思路：

从名为Users的表中选择user_id, name, mail这三个字段，并使用正则表达式来筛选出以字母开头，后面跟着字母、数字、下划线、点或连字符的字符串，最后以@leetcode.com结尾的邮箱地址

代码：

select  user_id, name, mail
from Users
-- 转义了`@`字符，因为它在某些正则表达式中具有特殊意义
where mail regexp '^[a-zA-Z][a-zA-Z0-9_.-]*\\@leetcode\\.com$'; -- 匹配以字母开头，后面跟着字母、数字、下划线、点或连字符的字符串，最后以`@leetcode.com`结尾的邮箱地址