题目链接

重新规划路线

题目描述

注意点

• 题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0
• 2 <= n <= 5 * 10^4
• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

解答思路

• 最初想到的是广度优先遍历根据当前能到达城市0的城市cities推出其他经过cities的城市，期间如果改变方向就能到达城市0或经过cities，则需要重新规划路线，结果加一，但是超时
• 参照题解使用深度优先遍历解决本题，首先需要存储能够到达任一城市i的所有城市，需要注意的是，如果城市i能够到达另一个城市j，那么城市j也可以到达城市i，只是需要改变方向，是否要改变方向取决于哪个城市能够到达城市0
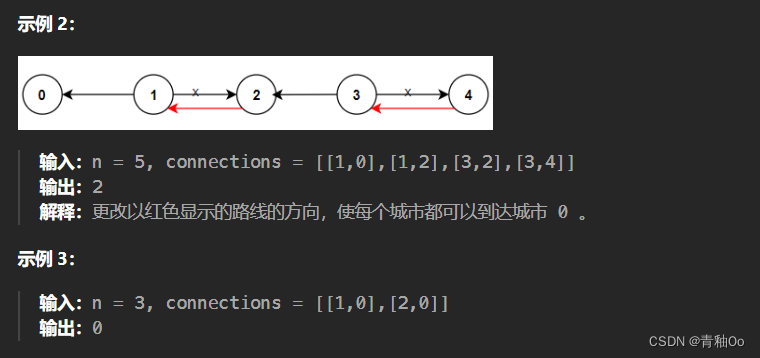
• 使用深度优先遍历反向推出能够到达城市0的相应城市，例如边为[[1,0],[1,2],[3,2],[2,4]]，能到达0的城市有1，到达1的城市有2（需改变方向），到达2的城市有3、4（需改变方向），将需要改变方向的数量相加就是需要重新规划路线的总数

代码

class Solution {
    public int minReorder(int n, int[][] connections) {
        // cityFront[i]对应的List表示能够到达城市i的所有城市
        List<int[]>[] cityFront = new List[n];
        for (int i = 0; i < n; i++) {
            cityFront[i] = new ArrayList<>();
        }
        for (int[] edge : connections) {
            int start = edge[0];
            int end = edge[1];
            // end到start需要改变方向
            cityFront[start].add(new int[]{end, 1});
            // start到end不需要改变方向
            cityFront[end].add(new int[]{start, 0});
        }
        return dfs(0, -1, cityFront);
    }

    public int dfs(int target, int parent, List<int[]>[] cityFront) {
        int sum = 0;
        // city是能到达target的所有城市
        for (int[] city : cityFront[target]) {
            // 当前判断的是target到达parent的情况，如果又深搜parent到target，则会死循环
            if (city[0] == parent) {
                continue;
            }
            // city[1]->从city到target是否要更改方向，深搜dfs->所有和city相连的城市中需要更改几次方向
            sum = sum + city[1] + dfs(city[0], target, cityFront);
        }
        return sum;
    }
}

关键点

• 使用List<int[]>[]结构存储能够到达城市i的所有城市（包括是否需要改变方向的信息），其中cityFront[i]对应的list表示能够到达城市i的所有城市，list.get(x)[0]表示能够到达城市i的第x个城市名，list.get(x)[1]表示到达城市i的第x个城市是否需要改变方向
• 需要传入城市target到达的parent，如果遍历到达target的城市中又有parent，则需要跳过，避免继续深搜导致死循环