3D模型实时变形算法

最近，在尝试渲染一些奇怪的形状后，我陷入了计算机图形学的困境。事实证明，对于我试图解决的具体问题，没有现有的选项完全适合我想要做的事情。几周后，我终于带着一些答案再次浮出水面，写了很多行代码！亲爱的读者，我现在将拉着你一起去。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割

1、我的目标

基本上，我想采用 3D 形状并在 WebGL 中将其扭曲制作动画。具体来说，我想结合以下三方面的内容：

输入形状：例如平面、球体、文件中的 3D 模型等。
畸变函数：给定空间中的一个点，告诉我该点偏移多少
材质：使用任何光照模型渲染形状（是否有光泽？是否用彩虹渐变着色？）

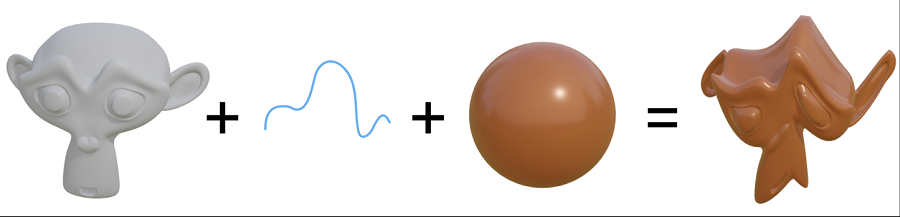
形状+变形+材质=无尽的时间沉没！

我为什么要这个？主要是因为它看起来很酷，但也因为它将是一个非常灵活的创意编码框架。输入形状+畸变函数+材质的不同组合可以产生各种各样的视觉结果。在 WebGL 中实时执行此操作而不是使用 Blender 节点执行此操作意味着它也可以是交互式的，这是一个优点。

不过，我不只是希望它能在 WebGL 中工作。我希望它能够与 p5.js 一起使用，p5.js 是一个非常通用的 Web 图形库。它比用于 3D 任务的 Three.js 之类的东西受到更多限制，但它使 2D 和 3D 画布之间的互操作变得更加容易。但是，p5 不提供用于在网格中传递附加顶点属性的 API。它可以通过直接挂钩底层 WebGL 调用来完成，但对我来说理想的解决方案只能利用顶点着色器中提供的标准信息：位置、法线、纹理坐标和对象/相机变换矩阵。

2、存在什么问题？

事实证明，采用任何形状+任何扭曲函数并使其适用于任何材料是相当困难的。该问题与表面法线有关。让我们快速回顾一下它们是什么以及它们为何如此重要。

2.1 使用法线渲染

在典型的 WebGL 渲染管道中，你通过顶点着色器发送形状信息，然后通过片段着色器发送形状信息，然后图像到达屏幕上。顶点着色器处理形状中的每个顶点，计算它在屏幕上的最终位置以及一些其他属性，例如该点的纹理坐标，以及法线，即该点远离表面的方向。在网格的每个三角形内部，这些属性会根据每个角的属性自动为每个像素进行插值，并发送到片段着色器，在其中它们用于查找像素的颜色。

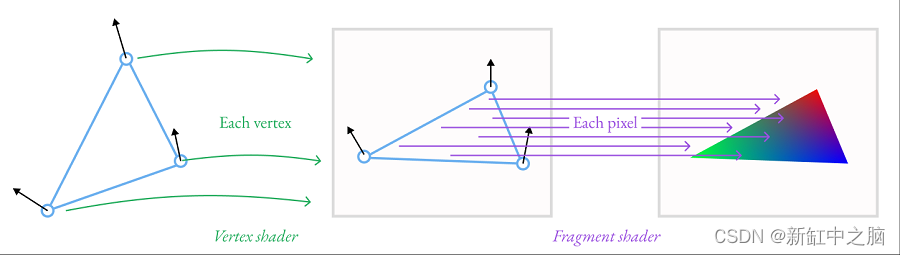
顶点通过顶点着色器放置在屏幕上的位置，片段着色器计算这些顶点之间的每个像素的颜色。

在片段着色器中，法线对于计算着色非常重要。材质基色的亮度取决于表面是否面向光线：如果直接指向光线，则接收到完全直射光；当它偏离时，接收到的光线越来越少，直到它面向 90 度或更大，此时它接收不到直射光。法线告诉我们表面面向的方向，因此我们使用它来执行此计算。当表面具有反射性时，我们也会使用法线，因为它告诉我们表面的方向，以及光线如何从表面反射。

2.2 扭曲后法线

3D 模型通常带有为每个顶点预先计算的法线，并且顶点着色器不需要对它们做太多操作。如果对象已在场景中旋转，则可能需要将相同的旋转应用于法线，但除此之外，它只是将其传递给片段着色器。

不幸的是，当你扭曲形状而不是仅仅严格旋转它时，事情会变得更加复杂。想象一下，取一个平面，然后用正弦波扭曲它。未扭曲的平面的法线全部面向同一方向。扭曲的平面现在具有指向许多不同方向的表面，具体取决于它们落在波浪上的位置。

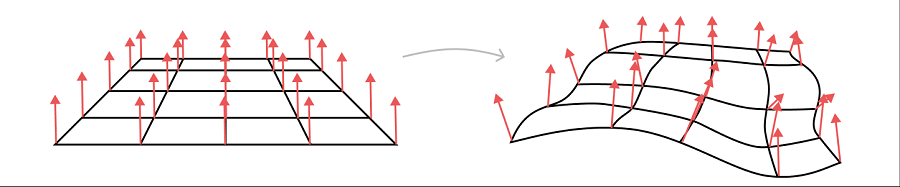
扭曲网格中的顶点后，原始法线可能不再正确

我们可以想象这个效果。这里我们有两个形状，左侧法线未更改，右侧法线已更改。这里的颜色代表它认为表面指向的方向：红色表示它指向左/右，绿色表示它指向上/下，蓝色表示它面向屏幕/面向屏幕外：

如果忽略由于扭曲而导致的法线变化，阴影看起来会明显错误。如果单击并拖动，你可以看到左侧未更改的法线斑点上的反射并没有按照预期的方式跟随凹凸：

3、简单的修复方法不起作用

所以我们知道我们必须对法线做一些事情。我们有什么选择？

3.1 自动片段着色器衍生品

核心问题是从顶点着色器发送的法线是错误的。那么，如果我们忽略它们并尝试完全在片段着色器中找出法线呢？

可以使用两个表面切线的叉积找到表面法线。如果表面位置 p 可以通过两个变量 u 和 v 以某种方式参数化，则表面法线为：

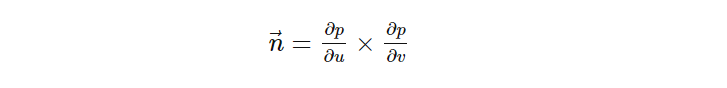
方便的是，在片段着色器中，我们可以通过 x 和 y 中的像素位置来参数化表面位置！ GLSL 提供了函数 dFdx(some_variable) 和 dFdy(some_variable)，它们可以查看水平相邻像素和垂直相邻像素中变量的值，并告诉你其值发生了多少变化。通过在位置变量上使用这些函数，我们可以获得表面在两个方向上的斜率。每个斜率都是沿 x 或 y 轴与表面相切的矢量。我们可以计算表面法线作为它们的叉积：

attribute vec3 position;
uniform vec3 baseColor;

void main() {
  vec3 normal = normalize(cross(dFdx(position), dFdy(position)));

  // Now use the normal for lighting, e.g. Lambertian diffuse shading
  vec3 toLight = vec3(0.0, 0.0, 1.0);
  float brightness = max(dot(normal, toLight), 0.0);
  gl_Fragcolour = vec4(brightness * baseColor, 1.0);
}

到目前为止，一切都很好！但我们的结果有问题。如果我们使用法线方向作为形状的颜色来为形状着色，效果如下：

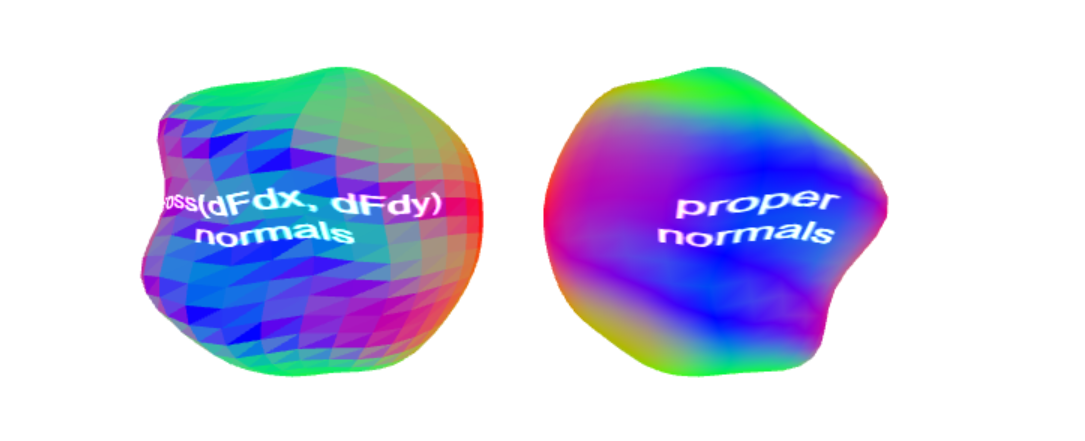
我们看到的多面阴影是由于法线在表面上变化不平滑造成的。法线不会平滑变化，因为表面本身实际上并不平滑：它由三角形组成，我们从这些三角形中获得法线。表面之前看起来只是平滑的，因为 WebGL 管道正在为每个三角形上的每个像素插入从顶点着色器发送的法线。由于我们自己重新计算法线，因此我们在这里无法获得平滑的法线插值。

3.2 手动顶点着色器衍生品

好的，如果我们希望在到达片段着色器的过程中对法线进行平滑插值，我们需要在顶点着色器中计算法线。我们想要做与之前尝试的基本相同的事情，获取两个曲面切线的叉积，但这次是在顶点着色器中。

然而，在顶点着色器中，我们不再有 dFdx 和 dFdy 函数了！如果我们想要导数，我们就必须自己写！

这本质上并不是一个问题。没有任何技术限制可以阻止我们编写失真函数的导数，然后我们可以用它来计算调整后的法线。限制在于我的键盘和椅子之间。作为一项破冰活动，当人们问我想要什么超能力时，我的首选答案是我希望能够第一次、每次都正确地做代数。不幸的是，我没有这种超能力，所以当我必须为相对复杂的失真函数编写导数时，我会忘记某处的减号，并且我会浪费几个小时来调试它。因此，出于这个原因，我将否决将此称为“解决方案”。

4、核心方案：自动生成着色器代码

我否决手写导数不是因为计算导数是一门艺术，而是因为它实际上是一个必须遵循的相当严格的算法，而我易犯错误的人类大脑不擅长遵循严格的算法。但你知道遵循严格算法的好处是什么吗？一台电脑。那么，如果我们让计算机来编写导数呢？

4.1 自动微分架构

计算函数相对于某个变量的导数是一种相当简单的递归算法。这是你可能在高中时学到的。每个基本操作都有一个预定义的导数。

例如， ∂sin(x)/∂x=cos(x)。如果某个运算应用于某个更复杂的函数 u，则我们使用递归链式法则，将正弦运算的导数乘以 u 的导数： ∂sin(u)/∂x = cos (u) ∂u/∂x。你只需继续深入工作，从最外层的操作向内进行，直到你无法进一步分解为止。

以面向对象的方式对此进行建模，每个操作都将是一个知道如何计算其自身导数的对象。它的参数本身可以是导数运算。像 0.1 * (sin(10*x + 20))^2 这样的表达式将转换为如下所示的对象层次结构：

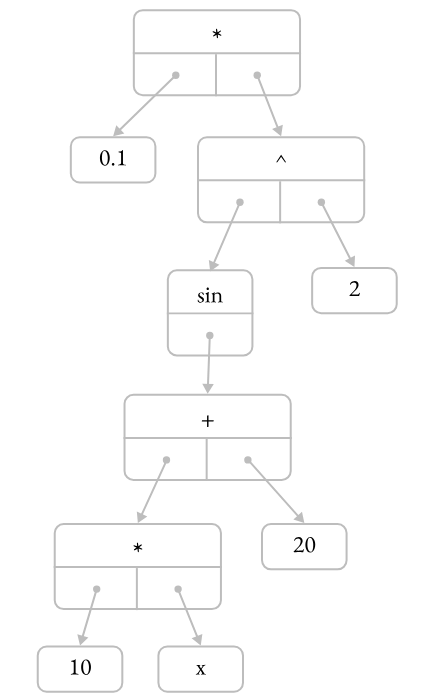
0.1 * (sin(10*x + 20))^2 的语法树细分

sin 运算的实现可能如下所示，其中包含生成表示其值的代码以及表示其导数值的代码的方法，这两者都在其参数上递归调用函数：

class Sin {
  constructor(u) {
    this.u = u;
  }

  code() {
    return `sin(${u.code()})`
  }

  derivativeCode() {
    `cos(${u.code()}) * ${u.derivativeCode()}`
  }
}

然后，你可以通过拼接 derivativeCode()的输出来在着色器中使用它：

const sinOp = new Sin( /* TODO build up tree of operations here */ );
const vert = `
  uniform mat4 uModelViewMatrix;
  uniform mat4 uProjectionMatrix;
  attribute vec3 position;

  void main() {
    vec3 newPosition = position;
    newPosition.y += ${sinOp.code()};

    float deriv = ${sinOp.derivativeCode()};
    // TODO do something with deriv here

    gl_Position = uProjectionMatrix * uProjectionMatrix * vec4(newPosition, 1.0);
  }
`;

然后，如果你通过构建运算树编写想要求导数的代码，还可以免费生成计算导数的代码！

当然，通过构造代表每个操作的对象来编写代码可能会很乏味。我直接知道这一点：我在滑铁卢读本科时的第四年设计项目想法的早期原型让我这样做，这是我们放弃该项目想法的主要原因之一。

一种选择可能是让你将 GLSL 代码编写为字符串，将该字符串解析为语法树，然后将语法树中的每个节点映射到一个操作。这个选项很好，但实施起来需要大量工作。作为妥协，我选择使用类似构建器的设计模式和可链接的方法，以使编写变得不那么冗长。由于操作对象也是普通的 Javascript 对象，因此它们也可以在循环和条件中分配和重新分配 —从生成的 GLSL 的角度来看，使用的任何 Javascript 代码都像宏一样。

我创建的库可在 NPM 上以 @davepagurek/glsl-autodiff 的形式获取。这也是本页上“正确法线”示例的动力！它允许你编写一些表达式，然后根据输入变量获取这些表达式的导数。以下是使用最终库的片段：

import { gen } from '@davepagurek/glsl-autodiff';

const vert = `
  void main(void) {
    vec4 objSpacePosition = vec4(aPosition, 1.0);

    float x = objSpacePosition.x;
    float y = objSpacePosition.y;
    ${gen((ad) => {
      const x = ad.param('x');
      const y = ad.param('y');
      const time = ad.param('time');
      const speedX = 1.5;
      const speedY = 2.8;

      let offset = ad.val(0);
      for (let i = 0; i < 3; i++) {
        offset = offset.add(ad.sin(
          ad.sum(
            offset.mult(0.5).add(x.mult(speedX)).add(y.mult(speedY)),
            time.mult(0.002),
          )
        ));
      }
      offset = offset.mult(0.1);
      offset.output('z');
      offset.outputDeriv('dzdx', x);
      offset.outputDeriv('dzdy', y);
    })}
    objSpacePosition.z = z;
    vec3 tangentX = vec3(1.0, 0.0, dzdx);
    vec3 tangentY = vec3(0.0, 1.0, dzdy);
    vNormal = uNormalMatrix * normalize(cross(tangentX, tangentY));

    vec4 worldSpacePosition = uModelViewMatrix * objSpacePosition;
    gl_Position = uProjectionMatrix * worldSpacePosition;
  }
`;

5、我们实际上用这些衍生品做什么？

太棒了，我们现在可以编写一个失真函数并自动获得导数。我们如何利用这些衍生品来获得我们一直在拼命寻找的常态？

5.1 使平面变形

我从一个简单但仍然实用的案例开始：在一维上扭曲平面。

给定平面上的 x 和 y 位置，我将提供一个生成新 z 值的函数。这个设置是一个很好的起点，因为我们可以通过获取 x 和 y 的导数来轻松得出两个曲面切线，就像我们在片段着色器中所做的那样。

使用 glsl-autodiff，我们可以将以下内容拼接到顶点着色器中，以获得 x 和 y 中的位移及其导数：

gen((ad) => {
  const position = ad.vec3Param('position');

  // Imagine we have a displace() function, generating offset based on x and y
  const offset = displace(position.x(), position.y());

  offset.output('offset');
  offset.outputDeriv('doffset_by_dx', position.x());
  offset.outputDeriv('doffset_by_dy', position.y());
})

现在我们需要从中获得表面法线。如果平面表面上的原始位置为 p，新的偏移量为 k，则扭曲位置为 p′= p + [0 0 k]T。由于我们的输入是一个平面，我们还知道原始位置相对于 x 和 y 的导数相当简单（在这种情况下，x 和 y 导数只是分别指向 x 或 y 方向的单位向量）。正常情况下的数学计算结果如下：

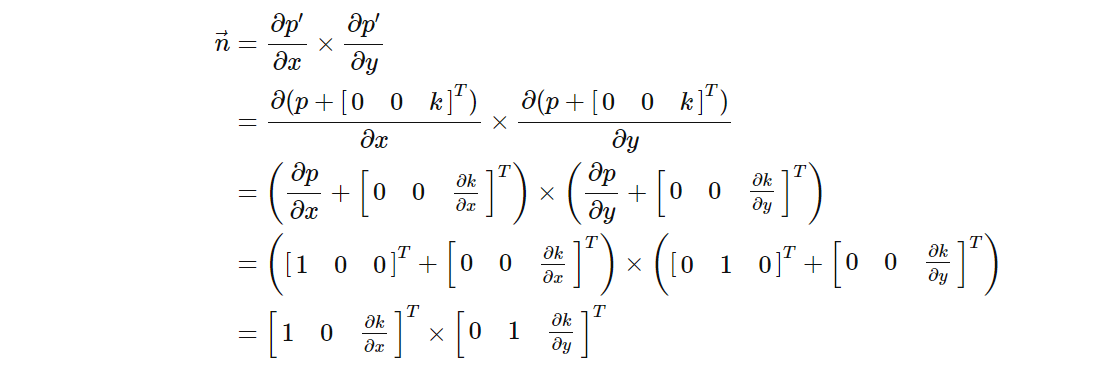
由于位移直接给出了两个表面切向量，因此我们可以通过将它们交叉来轻松获得法线。

这是使用自动差异输出变量 doffset_by_dx 和 doffset_by_dy 在着色器的其余部分中的外观：

// Use the offset
vec3 outPosition = position;
outPosition.z += offset;

// The normal is the cross product of two surface tangents, which are
// the changes in z given a unit change in our two surface directions
vec3 tangentX = vec3(1., 0., doffset_by_dx);
vec3 tangentY = vec3(0., 1., doffset_by_dy);
vec3 normal = normalize(cross(tangentX, tangentY));

5.2 使具有现有法线的形状变形

当你在开始时并不平坦的输入形状上使用相同的 x, y => z 位移时，事情会变得更加复杂。平面恰好很容易由 x 和 y 参数化，让我们很容易获得方向导数，但任何任意输入形状可能都不是。

仔细阅读维基百科有关计算表面法线的文章并没有多大帮助，因为它主要关注由函数定义的形状。如果我们有一个定义完整形状的函数，我们可以对该函数对两个参数求导。但在顶点着色器内部，除了两条信息之外，我们无法对表面的形状做出任何假设：当前顶点的位置及其现有法线。我们只有形状位移的函数。 Morten Mikkelsen 于 2010 年发表的一篇论文很接近：它描述了如何计算任意表面上任意凹凸贴图的法线，但仅限于使表面沿表面法线方向变形不同量的凹凸贴图。在我们的例子中，我们的位移方向可能与表面法线方向完全无关。

我找到的解决方案是计算位移引起的法线的旋转，然后将其应用于输入法线。对于给定的位置，想象我们从一个平面开始，然后扭曲该平面。我们知道平面的法线从指向 z 方向开始，然后最终指向 cross(tangentX, tangentY) 方向。我们可以计算这两个向量之间的旋转，然后将相同的旋转应用于非平面网格的原始法线！

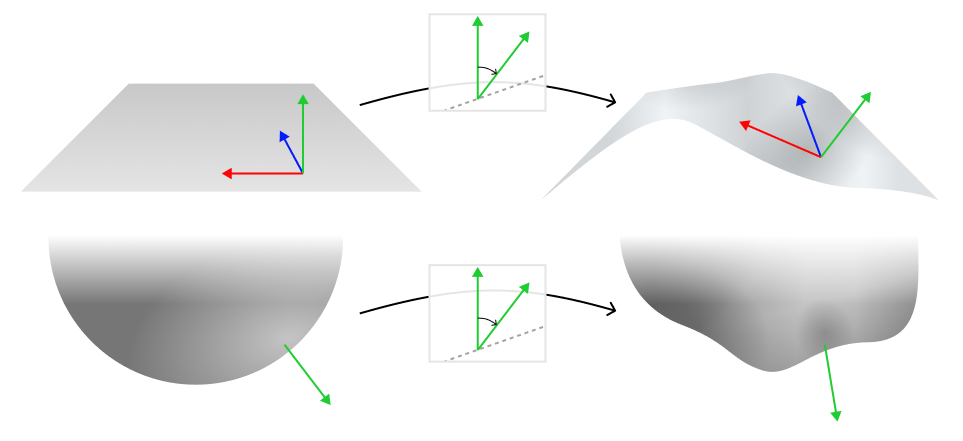
如果我们想象一个平面正在变形，我们可以计算变形引起的法线旋转。然后我们可以将相同的旋转应用于任何其他形状的初始表面法线。

任意两个向量 v1 和 v2 之间的角度为 cos−1(v1⋅v2)。在这种情况下，旋转轴将是垂直于两个输入向量的向量，我们可以通过 v1×v2 得到它。使用这个轴和角度，我们可以构造一个旋转矩阵，它将相同的旋转应用于与之相乘的任何向量。这是 GLSL 中的样子：

// Assume we have a function to generate an axis/angle rotation matrix:
mat4 axisAngleRotation(vec3 axis, float angle) { /* ... */ }
// See http://www.neilmendoza.com/glsl-rotation-about-an-arbitrary-axis for an implementation

// Compute a normal like before, as if the mesh were a plane
vec3 tangentX = vec3(1., 0., doffset_by_dx);
vec3 tangentY = vec3(0., 1., doffset_by_dy);
vec3 displacedPlaneNormal = normalize(cross(tangentX, tangentY));

// The un-displaced normal for our hypothetical plane. This is the result
// of crossing the undistorted surface normals: cross(vec3(1.,0.,0.), vec3(0.,1.,0.))
vec3 originalPlaneNormal = vec3(0., 0., 1.);

// Find the rotation induced by the displacement
float angle = acos(dot(originalPlaneNormal, noDisplacementNormal));
vec3 axis = normalize(cross(originalPlaneNormal, noDisplacementNormal));
mat4 rotation = axisAngleRotation(axis, angle);

// Apply the rotation to the original normal
vec3 normal = (rotation * vec4(origNormal, 0.)).xyz;

5.3 使形状在三个维度上变形

我们需要做出的最后一步是支持不仅仅是 z 轴上的扭曲，将完整的顶点位置作为输入并生成完整的 3D 向量作为输出（我将其称为矢量k，而不是我们的标量 k）之前）。

由于我们需要获得两个曲面切线的叉积，因此我们将再次需要两个方向导数。以前，由于失真仅取决于 x 和 y，因此用于方向导数的明显轴是 x 和 y。但由于我们现在依赖于 x、y 和 z，因此我们需要导数来考虑所有这三个因素。解决这个问题的一种方法是使用 x 和 u 作为轴，其中我们定义 u=y+z。

为了获得关于 u 的导数，我们可以查看位移函数的雅可比行列式，其中 J=[∂k/∂x ∂k/∂y ∂k/∂z]，每个偏导数都给我们一个现在位移 k 是一个 3D 向量。雅可比矩阵与方向向量的点积给出了该方向向量的方向导数。在我们的例子中，关于 u 的导数最终只是 y 和 z 导数之和：

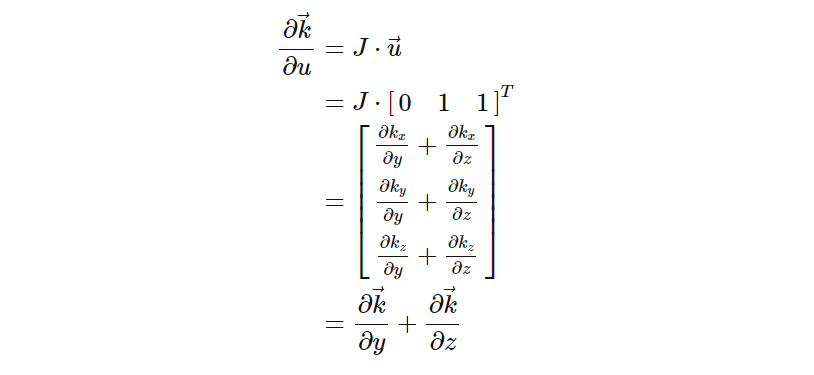
现在我们可以用它来进行数学计算以获得正常值。平面相对于 u 的导数又很简单，就是 [0 1 1]。正常的结果如下：

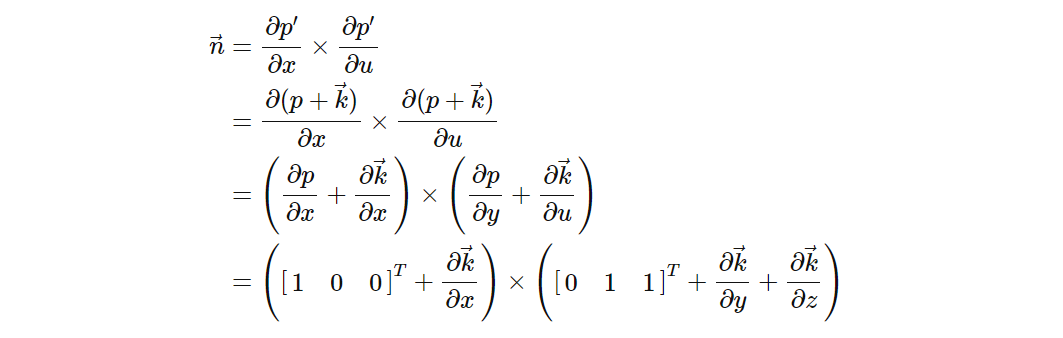
我向自己证明，这与我们的一维变形法线一致，因为以前，我们的斜率向量具有轴向量加上由于该轴的变化而产生的位移的形式。之前我们的位移恰好位于与我们方向正交的轴上，例如 x 轴斜率 [1 0 0]T + [0 0 ∂k/∂x]T。碰巧的是，现在我们的位移向量可能在方向向量的轴上具有非零分量，但我们仍然具有相同的形式：[1 0 0]T + ∂k/∂x。

此计算的 GLSL 版本看起来与之前非常相似：

// doffset_by_d{x,y,z} are all vec3s now instead of a floats
vec3 tangentX = vec3(1., 0., 0.) + doffset_by_dx;
vec3 tangentYZ = vec3(0., 1., 1.) + doffset_by_dy + doffset_by_dz;
vec3 displacedPlaneNormal = normalize(cross(tangentX, tangentY));

// The un-displaced normal for our hypothetical plane
vec3 originalPlaneNormal = normalize(cross(vec3(1., 0., 0.), vec3(0., 1., 1.));

// Everything from here on is the same as before!

// Find the rotation induced by the displacement
float angle = acos(dot(originalPlaneNormal, noDisplacementNormal));
vec3 axis = normalize(cross(originalPlaneNormal, noDisplacementNormal));
mat4 rotation = axisAngleRotation(axis, angle);

// Apply the rotation to the original normal
vec3 normal = (rotation * vec4(origNormal, 0.)).xyz;

...就是这样！这就是我们需要的着色器代码，以实现采用任意形状、扭曲和材质并使法线正常工作的目标。