目录
leetcode题目
一、最大子数组和
二、环形子数组的最大和
三、乘积最大子数组
四、乘积为正数的最长子数组长度
五、等差数列划分
六、最长湍流子数组
七、单词拆分
八、环绕字符串中唯一的子字符串
子数组系列，属于线性dp问题，状态表示也是之前提到的以某个位置元素为结尾分析问题，而状态转移方程也是有规律的，一般就是长度为1和长度>1来划分问题，进而得出状态转移方程
leetcode题目
一、最大子数组和
53. 最大子数组和 - 力扣（LeetCode）
https://leetcode.cn/problems/maximum-subarray/1.题目解析
找到和最大的子数组，返回该子数组的和
2.算法分析
1.状态表示
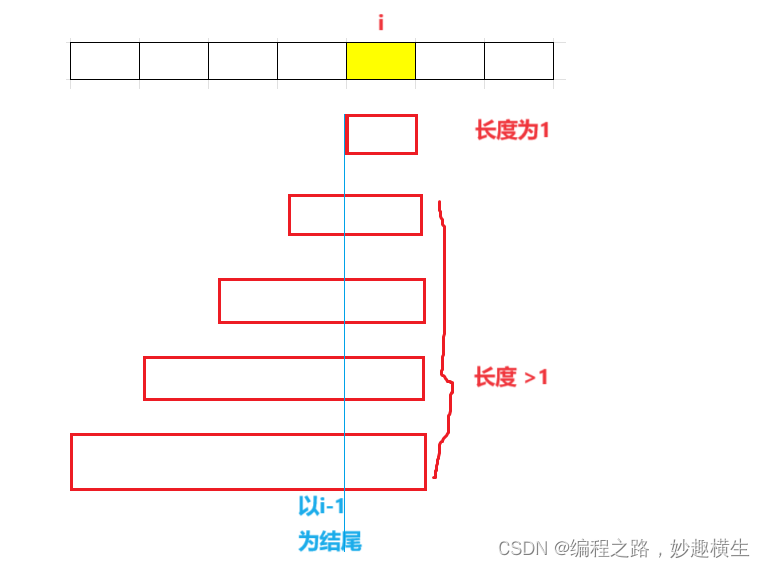
dp[i] 表示 以 i 位置元素为结尾的所有子数组的最大和
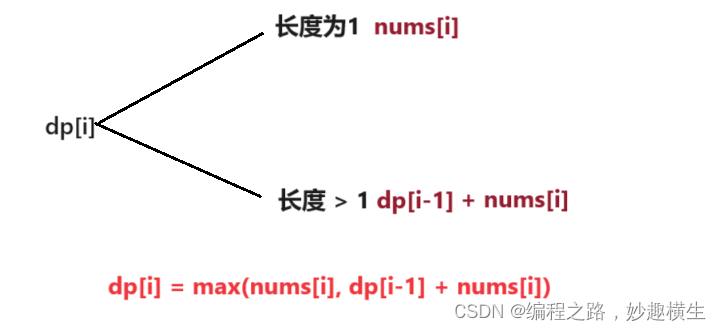
2.状态转移方程
3.初始化
添加虚拟节点, 注意下标的映射关系
dp[0] = 0
4.填表
从左向右
5.返回值
dp表中的最大值
3.算法代码
class Solution {
public:
int maxSubArray(vector<int>& nums)
{
//1.创建dp表
int n = nums.size();
vector<int> dp(n+1);
//2.初始化dp表
dp[0] = 0; //vector默认是0, 可以不写
//3.填表 + 返回值
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
dp[i] = max(nums[i-1], dp[i-1] + nums[i-1]);
ret = max(ret, dp[i]);
}
return ret;
}
};二、环形子数组的最大和
918. 环形子数组的最大和 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-sum-circular-subarray/description/1.题目解析
与题目一的区别就是本题的数组是环形数组， 因此子数组的选取情况变多了~
2.算法分析
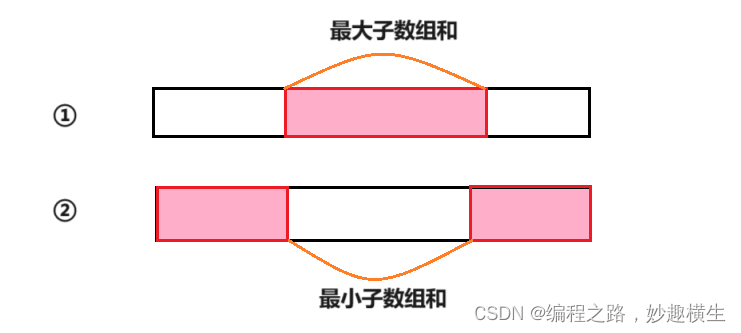
本题的最大子数组和无非两种情况: 第一种情况直接求最大子数组和即可，而第二种情况可以转化成求中间连续部分的最小子数组和~
1.状态表示
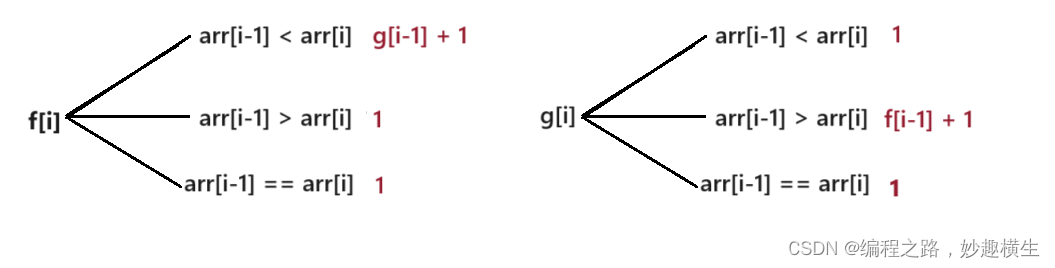
f[i]： 以 i 位置为结尾的所有子数组中的最大和
g[i]： 以 i 位置为结尾的所有子数组中的最小和
2.状态转移方程
f[i] = max(nums[i], f[i-1]+nums[i])
g[i] = min(nums[i], g[i-1]+nums[i])
3.初始化
添加虚拟节点, 注意下标的映射关系
dp[0] = 0, g[0] = 0
4.填表
从左向右
5.返回值
①找到f表的最大值 -> fmax
②找到g表的最小值 -> gmin -> sum-gmin
返回①，②两种情况的最大值，但是当数组元素全为负数是有问题的，因此我们需要判断!
sum == gmin ? fmax : max(fmax, sum-gmin)
3.算法代码
class Solution{
public:
int maxSubarraySumCircular(vector<int>& nums)
{
//1.创建dp表
int n = nums.size();
vector<int> f(n+1), g(n+1);
//2.初始化dp表
f[0] = 0, g[0] = 0; //vector默认是0, 可以不写
//3.填表 + 返回值
int fmax = INT_MIN, gmin = INT_MAX, sum = 0;
for(int i = 1; i <= n; i++)
{
sum += nums[i-1];
f[i] = max(nums[i-1], f[i-1] + nums[i-1]);
fmax = max(fmax, f[i]);
g[i] = min(nums[i-1], g[i-1] + nums[i-1]);
gmin = min(gmin, g[i]);
}
return sum == gmin ? fmax : max(fmax, sum-gmin);
}
};三、乘积最大子数组
152. 乘积最大子数组 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-product-subarray/1.题目解析
返回乘积最大的子数组的乘积
2.算法分析
1.状态表示
f[i] : 以 i 位置为结尾的所有子数组中的最大乘积
g[i] : 以 i 位置为结尾的所有子数组中的最小乘积
2.状态转移方程
3.初始化
添加虚拟节点, 注意下标的映射关系
f[0] = g[0] = 1
4.填表
从左向右两个表一起填
5.返回值
f表的最大值
3.算法代码
class Solution {
public:
int maxProduct(vector<int>& nums)
{
//1.创建dp表
int n = nums.size();
vector<int> f(n+1), g(n+1);
//2.初始化dp表
f[0] = g[0] = 1;
//3.填表 + 返回值
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
f[i] = max(nums[i-1], max(f[i-1]*nums[i-1], g[i-1]*nums[i-1]));
g[i] = min(nums[i-1], min(g[i-1]*nums[i-1], f[i-1]*nums[i-1]));
ret = max(ret, f[i]);
}
return ret;
}
};四、乘积为正数的最长子数组长度
1567. 乘积为正数的最长子数组长度 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/description/1.题目解析
求乘积为正数的最长子数组的长度
2.算法分析
1.状态表示
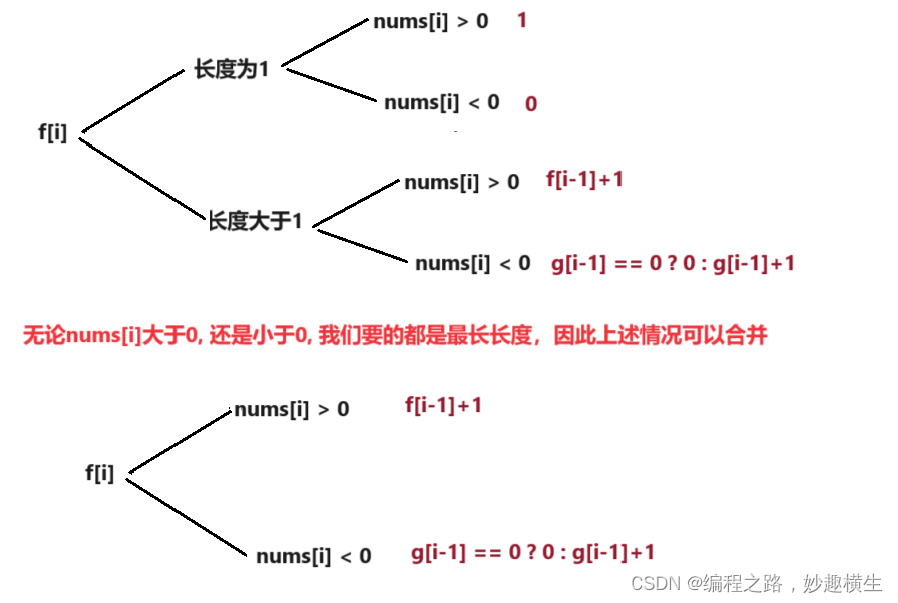
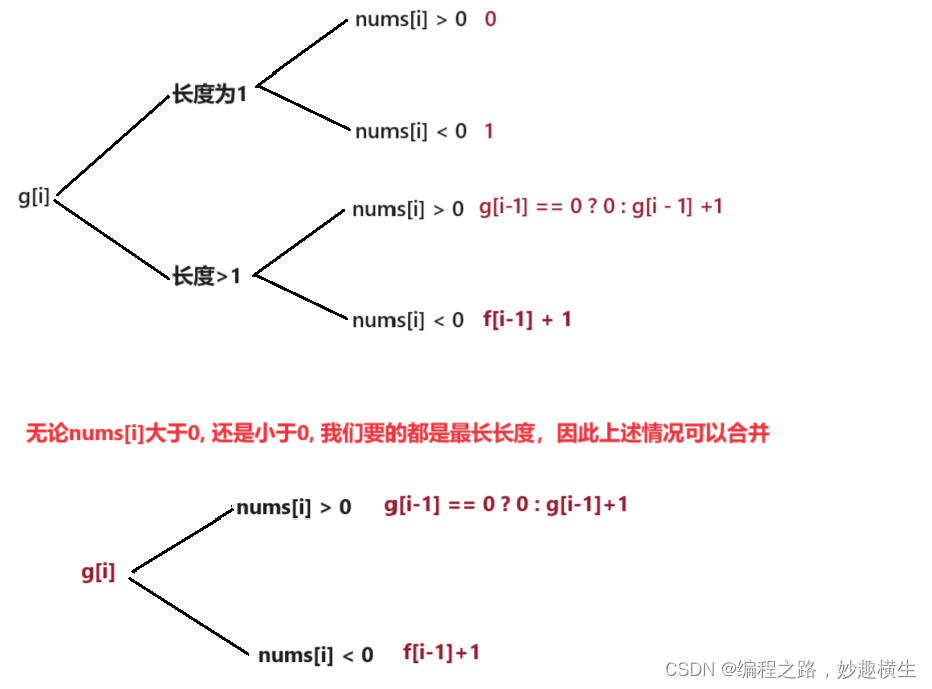
f[i]: 以 i 位置为结尾的所有子数组中乘积为正数的最长长度
g[i]: 以 i 位置为结尾的所有子数组中乘积为负数的最长长度2.状态转移方程
3.初始化
添加虚拟节点, 注意下标的映射关系
f[0] = 0, g[0] = 0
4.填表
从左向右两个表一起填
5.返回值
f表的最大值
3.算法代码
class Solution {
public:
int getMaxLen(vector<int>& nums)
{
//1.创建dp表
int n = nums.size();
vector<int> f(n+1), g(n+1);
//2.初始化dp表
f[0] = g[0] = 0; //vector默认是0, 可以不写
//3.填表 + 返回值
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
if(nums[i-1] > 0)
{
f[i] = f[i-1] + 1;
g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
}
if(nums[i-1] < 0)
{
f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
g[i] = f[i-1] + 1;
}
ret = max(ret, f[i]);
}
return ret;
}
};五、等差数列划分
413. 等差数列划分 - 力扣（LeetCode）https://leetcode.cn/problems/arithmetic-slices/1.题目解析
返回数组中等差数组的个数
2.算法分析
小性质: [a, b, c, d] 是等差数列，[c, d, e]构成等差数列，则[a, b, c, d, e]是等差数列
1.状态表示
dp[i]： 以 i 位置为结尾的所有子数组中等差数列的个数
2.状态转移方程
3.初始化dp[0] = dp[1] = 0
4.填表
从左向右
5.返回值
返回dp表中所有元素之和
3.算法代码
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums)
{
//1.创建dp表
int n = nums.size();
vector<int> dp(n);
//2.初始化
dp[0] = dp[1] = 0; //vector默认是0, 可以不写
//3.填表 + 返回值
int ret = 0;
for(int i = 2; i < n; i++)
{
dp[i] = nums[i] - nums[i-1] == nums[i-1] - nums[i-2] ? dp[i-1] + 1 : 0;
ret += dp[i];
}
return ret;
}
};六、最长湍流子数组
978. 最长湍流子数组 - 力扣（LeetCode）https://leetcode.cn/problems/longest-turbulent-subarray/1.题目解析
数组中相邻元素对之间的大小关系相反，这就是湍流数组，题目要求返回数组中最长的湍流子数组的长度
2.算法分析
1.状态表示
f[i]：以 i 位置为结尾的所有子数组中，最后呈现 "上升" 状态下的最长的湍流子数组的长度
g[i]：以 i 位置为结尾的所有子数组中，最后呈现 "下降" 状态下的最长的湍流子数组的长度
2.状态转移方程
3.初始化
把 f 表和 g 表所有的元素都初始化成1
4.填表顺序
从左往右两个表一起填
5.返回值
两个表的最大值
3.算法代码
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr)
{
//1.创建dp表
int n = arr.size();
vector<int> f(n, 1), g(n, 1);
//2.填表 + 返回值
int ret = 1;
for(int i = 1; i < n; i++)
{
if(arr[i-1] > arr[i])
g[i] = f[i-1] + 1;
if(arr[i-1] < arr[i])
f[i] = g[i-1] + 1;
ret = max(ret, max(f[i], g[i]));
}
return ret;
}
};七、单词拆分
139. 单词拆分 - 力扣（LeetCode）https://leetcode.cn/problems/word-break/1.题目解析
给定一个字符串和单词字典，判断使用字典中的单词(可以重复使用)是否可以拼接成功字符串
2.算法分析
1.状态表示
dp[i]: [0, i]区间内的字符串, 能否被字典中的单词拼接而成
2.状态转移方程
3.初始化
添加虚拟节点
dp[0] = true
下标的映射关系，可以给"原字符串"开始加一个空格, 这样dp表和原始字符串就是一一对应的
4.填表顺序
从左往右
5.返回值
dp[n]
3.算法代码
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict)
{
//优化:
unordered_set<string> hash;
for(auto& s : wordDict) hash.insert(s);
//1.创建dp表
int n = s.size();
vector<bool> dp(n+1);
//2.初始化
dp[0] = true;
s = ' ' + s;
//3.填表
for(int i = 1; i <= n; i++)
{
for(int j = i; j >= 1; j--)
{
if(dp[j-1] && hash.count(s.substr(j, i - j + 1)))
{
dp[i] = true;
break;
}
}
}
return dp[n];
}
};八、环绕字符串中唯一的子字符串
467. 环绕字符串中唯一的子字符串 - 力扣（LeetCode）https://leetcode.cn/problems/unique-substrings-in-wraparound-string/1.题目解析
给定一个base字符串，统计字符串s中有多少个不同的子串在base中出现过
2.算法分析
1.状态表示
dp[i]: 以 i 位置为结尾的所有子串中，有多少个在base中出现过
2.状态转移方程
3.初始化
将dp表里面所有的值都初始化成1， 因此dp[i] += dp[i-1] 即可
4.填表顺序
从左往右
5.返回值
以相同的字符为结尾的所有子串中，可能会出现重复的情况，比如:
"abcyzabc", 该子串中，以第一个字符'c'结尾的子串 abc 与 以第二个字符'c'结尾的子串abc就是重复的，因此我们需要去重(由于以第二个字符'c'结尾的所有子串一定是包含'abc'的，因此同一个字符结尾对应的dp值取最大的即可):
①创建一个大小为26的数组
②里面的值保存相应字符结尾的最大的dp值即可
最后返回 数组中所有元素的和即可
3.算法代码
class Solution {
public:
int findSubstringInWraproundString(string s)
{
//1.创建dp表
int n = s.size();
vector<int> dp(n, 1);
//2.填表
for(int i = 1; i < n; i++)
if(s[i-1] + 1 == s[i] || (s[i-1] == 'z' && s[i] == 'a'))
dp[i] += dp[i-1];
//3.返回值
int hash[26] = {0};
for(int i = 0; i < n; i++)
hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);
int sum = 0;
for(auto x : hash)
sum += x;
return sum;
}
};
