题目：

矩阵对角线 是一条从矩阵最上面行或者最左侧列中的某个元素开始的对角线，沿右下方向一直到矩阵末尾的元素。例如，矩阵 mat 有 6 行 3 列，从 mat[2][0] 开始的 矩阵对角线 将会经过 mat[2][0]、mat[3][1] 和 mat[4][2] 。

给你一个 m * n 的整数矩阵 mat ，请你将同一条 矩阵对角线 上的元素按升序排序后，返回排好序的矩阵。

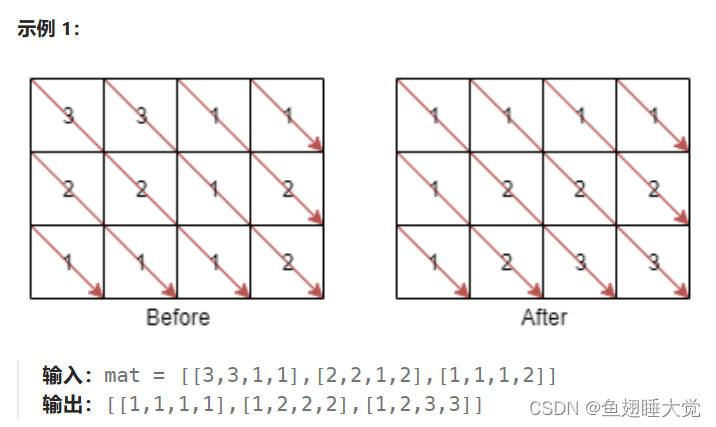
思考：

因为每一条对角线都彼此平行互不干扰，所以我们可以遍历每一条对角线上的元素，将其看成一个新数组，从小到大排序后填回原来矩阵中对应的位置。代码如下：

class Solution(object):
    def diagonalSort(self, mat):
        """
        :type mat: List[List[int]]
        :rtype: List[List[int]]
        """
        m = len(mat)
        n = len(mat[0])

        def diagonal(x, y, mat):
            # 遍历对角线上所有元素，看成一个新数组，从小到大排序
            diagonal_number = []
            i = x
            j = y
            while i < m and j < n:
                diagonal_number.append(mat[i][j])
                i += 1
                j += 1
            diagonal_number.sort()
            
            # 将排序后的元素填回矩阵
            index = 0
            i_ = x
            j_ = y
            while i_ < m and j_ < n:
                mat[i_][j_] = diagonal_number[index]
                index += 1
                i_ += 1
                j_ += 1
            return mat

        diagonals = []
        # 将第一行和第一列所有坐标都计入对角线起点列表diagonals中
        for p in range(n):
            diagonals.append((0, p))
        for q in range(1, m):
            diagonals.append((q, 0))

        # 遍历每一条对角线
        for diag in diagonals:
            diagonal(diag[0], diag[1], mat)

        return mat

提交通过：