递归与递推---题目练习

news2024/11/24 7:59:52

目录

1、递归实现指数型枚举

2、递归实现排列型枚举

3、递归实现组合型枚举

4、带分数

方法一

方法二

5、翻硬币

6、飞行员兄弟

7、费解的开关

递归是指在函数的定义中使用函数自身的方法。它通过不断地将问题分解为更小的子问题，直到达到基本情况，然后再逐层返回结果。

递推则是通过已知的前一个或前几个状态来推导出后续状态的方法。它是按照一定的规律逐步计算出后续结果的过程。

从宏观上来看，递归是将一个大问题分解为多个相同类型的小问题，不断重复；递推是根据前一个或前几个状态逐步推出后续状态，也就是从小问题解决到大问题。

本文是递归与递推的算法题练习，题目都源于网站Acwing

1、递归实现指数型枚举

输入样例：

3

输出样例：


3
2
2 3
1
1 3
1 2
1 2 3

当每个状态的可能情况都是相同的，那么此时就是指数型枚举

在这种枚举方式中，通常会以某种特定的顺序或规则来遍历所有可能的情况

比如本题，枚举1~n的每个数，每个数都有选或不选两种情况，共有2^n种结果

代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 20;
int n;
bool st[N];//每个数的状态，默认为都不选

void dfs(int x)
{
    if(x > n) 
    {
        for(int i=1;i<=n;i++)
            if(st[i]) cout<<i<<" ";
        cout<<endl;
        return ;
    }
    
    //不选
    st[x] = false;
    dfs(x+1);
    
    //选
    st[x] = true;
    dfs(x+1);
}

int main()
{
    cin>>n;
    
    dfs(1);

    return 0;
}

2、递归实现排列型枚举

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

所谓排列，就是对给定的元素，按照不同顺序，排列出所有可能的情况，每个元素不重不漏

特点：有序、不重不漏

代码实现时一般会为排列元素开一个状态数组，来判定是否选过

本题就是对1~n的全排列

代码：

#include<bits/stdc++.h>
using namespace std;

const int N =20;
bool st[N];//状态数组，是否选过，默认没选
int ans[N];
int n;

void dfs(int x)
{
    if(x > n)
    {
        for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
        cout<<endl;
    }
    
    for(int i=1;i<=n;i++)
    {
        if(!st[i])
        {
            st[i] = true;
            ans[x] = i;
            dfs(x+1);
            
            st[i] = false;//还原现场
        }
    }
}

int main()
{
    cin>>n;
    dfs(1);
    return 0;
}

3、递归实现组合型枚举

输入样例：

5 3

输出样例：

1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5

组合是从给定的元素集合中，选取若干个元素组成一组，而不考虑元素的排列顺序。

 

组合只关注选取哪些元素，而不关心这些元素的具体排列方式。

在代码实现中，组合型枚举区别于排列型、指数型枚举，它需要传参来标记枚举顺序（每次枚举的起始位置），防止枚举重复，同样的，因为每次标记了起始位置，所以从起始位置开始都是未选取的元素，不再像排列型枚举那样开状态数组

代码：

#include<bits/stdc++.h>
using namespace  std;

const int N = 30;
int n,m;
int ans[N];

void dfs(int x,int start)
{
    if(x-1 + n-start + 1 < m) return;
    
    if(x > m)
    {
        for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
        cout<<endl;
        return ;
    }
    
    for(int i=start;i<=n;i++)
    {
        ans[x] = i;
        dfs(x+1,i+1);
        
        ans[x] = 0;//还原现场，本题其实可以不用，会自动覆盖
    }
}

int main()
{
    cin>>n>>m;
    
    dfs(1,1);
    
    return 0;
}

4、带分数

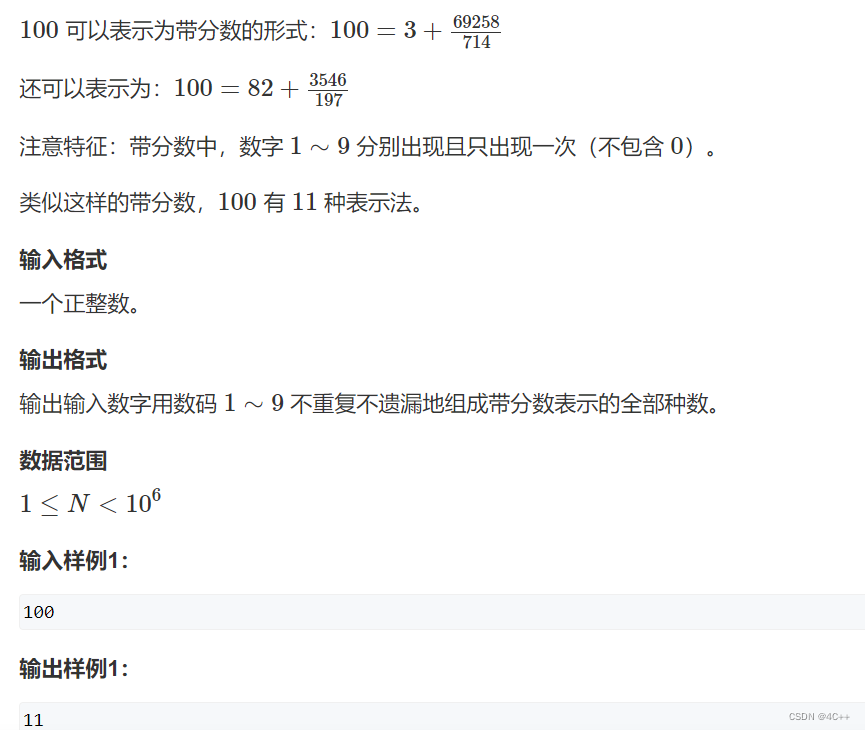
题意中的除法，没有特别指出时，一般都指正常的除法，而不是C++中的整除

题意表示，输入n，使得 n = a + b/c ，其中a、b、c包含的数字恰好为1~9各自出现一次

为了在编程时规避整除问题，我们一般把问题转化为乘法: n*c = a*c + b

方法一

每个元素恰好出现一次，正好对应全排列的性质，可以这么做：

  • 对1~9做全排列，共有 9！种情况
  • 枚举a、b、c分别有多少位（枚举了a、b就确定了c，两重循环即可）
  • 判断等式 n*c = a*c + b 是否相等

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10;
bool st[N];
int ans[N];
int n,cnt;

int to_nums(int l, int r)
{
    int res = 0;
    for(int i = l; i <= r; i++)
    {
        res = res*10 + ans[i];
    }
    return res;
}

void dfs(int x)
{
    if(x == 10)
    {
        for(int i = 1; i <= 7; i++)
        {
            for(int j = i+1; j<= 8; j++)
            {
                int a = to_nums(1,i);
                int b = to_nums(i+1,j);
                int c = to_nums(j+1,9);
                
                if(c*n == c*a + b) cnt++;
            }
        }
        
        return;
    }
    
    for(int i=1;i<=9;i++)
    {
        if(!st[i])
        {
            st[i] = true;
            ans[x] = i;
            dfs(x+1);
            
            st[i] = false;
        }
    }
}

int main()
{
    cin>>n;
    
    dfs(1);
    
    cout<<cnt<<endl;
    return 0;
}

方法一的做法虽然能够AC，但因为是全排列，罗列了所有的情况去判断，有没有更高效的做法呢？

方法二

对于等式：n*c = a*c + b ，要找出满足该等式的三个数a、b、c，在给定了n的情况下，其实只需要确定了a、c， 根据等式，b也就确定了，再用确定的一组a、b、c，去判断是否满足题目要求（三个数包含的数字有且只能1~9各出现一次），这样的做法，不会像全排列那样罗列所有情况，会更加高效

步骤：

  • 先搜索可能满足情况的数字a ( 0 < a < n)
  • 对于每一个a，再去搜索可能的c ( a、c用的数字个数小于9，c > 0 )
  • 对于每一组a、c，通过等式n*c = a*c + b计算得出b，再判断是否满足题意
  • 如何判断？先判断b的各个数字是否与a、c用的数字冲突，再怕判断1~9是否都被使用了

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 20;
bool st[N],backup[N];
int n,cnt;

bool check(int a, int c)
{
    long long b = c*(long long)n - c*a;
    if(!a || !b || !c) return false;
    
    memcpy(backup,st,sizeof st);
    
    while(b)
    {
        int t = b % 10;
        b /= 10;
        if(!t || backup[t]) return false;
        backup[t] = true;
    }
    
    for(int i=1; i <= 9; i++)
    {
        if(!backup[i]) return false;
    }
    
    return true;
}

void dfs_c(int x, int a, int c)
{
    if(x >= 9) return ;
    
    if(check(a,c)) cnt++;
    
    for(int i=1; i <= 9; i++)
    {
        if(!st[i])
        {
            st[i] = true;
            dfs_c(x+1,a,c*10+i);
            
            st[i] = false;
        }
    }
}

void dfs_a(int x,int a)
{
    if(a >=n) return ;
    if(a) dfs_c(x,a,0);
    
    for (int i = 1; i <= 9; i ++ )
    {
        if(!st[i])
        {
            st[i] = true;
            dfs_a(x+1,a*10+i);
            
            st[i] = false;
        }
    }
}


int main()
{
    cin>>n;
    
    dfs_a(0,0);
    
    cout<<cnt<<endl;
    return 0;
}

5、翻硬币

输入样例1：

**********
o****o****

输出样例1：

5

输入样例2：

*o**o***o***
*o***o**o***

输出样例2：

1

通过推演可以发现，我们只需用一个指针 i 从前向后扫描，如果当前 i 指向的位置初始状态和目标状态不同，就翻转 i 和 i+1 位置的硬币(并记录翻转次数+1)，保证 i 之前的初始状态和目标状态相同；因为题目说一定有解，如此遍历一遍，就一定能保证字符串的初始状态转变成了目标状态

代码：

#include<bits/stdc++.h>
using namespace std;

int main()
{
    string src,dst;
    cin >> src >> dst;
    
    int ans = 0;
    for(int i = 0; i < src.size(); i++ )
    {
        if(src[i] != dst[i])
        {
            src[i] = src[i] != '*' ? '*' : 'o';
            src[i+1] = src[i+1] != '*' ? '*' : 'o';
            ans++;
        }
    }
    
    cout << ans << endl;
    return 0;
}

6、飞行员兄弟

输入样例：

-+--
----
----
-+--

输出样例：

6
1 1
1 3
1 4
4 1
4 3
4 4

思路：题目数据是4 * 4的矩阵，对于每个开关我们可以有按或不按两种情况，也就是对于这个矩阵，枚举对矩阵的操作方案：共有2^16 可能；对于每种操作方案，去对矩阵操作一遍后判断是否满足题意（开关全开），保存操作次数最小的一种输出即可。

代码实现中，

  • 需要先枚举所有操作方案，每行用一个int数来代表，范围【0，15】；op[i]表示第 i 行的操作方案，所以需要对op[4]做指数型枚举，16^4种可能
  • 对于每一种操作方案，模拟一遍对矩阵的操作，所以需要一个备份矩阵backup，在每次矩阵操作、判断完成后，把被操作的矩阵恢复原样，方便下次操作
  • 矩阵的操作过程中，涉及到某个点的开关如果要按下，则需要用一个vector记录其坐标，方便后续输出；因为要更新最小值和对应得坐标，所以vector用tmp临时存储，如果要更新答案就把tmp赋值给ans，如果不更新答案就把tmp清空，以记录下一种操作方案的操作坐标

代码一：

#include<bits/stdc++.h>

using namespace std;


const int N = 20;
char g[N][N],backup[N][N];
int op[4];
bool st[16];
int ways = 50;

struct point
{
    int x;
    int y;
};

vector<struct point> tmp,ans;
void turn(int x, int y)
{
    for(int i = 0; i < 4; i++ )
    {
        g[x][i] = g[x][i] != '+' ? '+' : '-';
    }

     for(int i = 0; i < 4; i++ )
    {
        g[i][y] = g[i][y] != '+' ? '+' : '-';
    }

    g[x][y] = g[x][y] != '+' ? '+' : '-';
}


void check()
{
    int step = 0;
   
    for(int i = 0; i < 4; i++ )
    {
        for(int j = 0; j < 4; j++ )
        {
            if(op[i] >> j & 1)
            {
                step++;
                turn(i,j);
                tmp.push_back({i,j});
            }
        }
    }

    bool off = false;
    for(int i = 0; i < 4; i++ )
    {
        for(int j = 0; j < 4; j++ )
        {
            if(g[i][j] == '+')
            {
                off = true;
                break;
            }
        }
    }

    if(!off && (step < ways))
    {
        ways = min(ways,step);
        ans = tmp;
    }
    else
    {
        tmp.clear();
    }
    
    memcpy(g, backup, sizeof backup);
}


void dfs_op(int x)
{
    if(x == 4)
    {
        check();
        return ;
    }

    for(int i = 0; i < 16; i++ )
    {
       op[x] = i;
       dfs_op(x+1);
    }
}

int main()
{
    for(int i = 0; i < 4; i++ ) cin >> g[i];
    
     memcpy(backup, g, sizeof g);

    dfs_op(0);

    cout << ways << endl;
    for(auto& p : ans)
    {
        cout << p.x + 1 << " " << p.y + 1 <<endl;
    }
    return 0;
}

代码二：

这个版本，是枚举操作方案时，直接用一个int来表示4x4矩阵的开关操作，再通过映射函数来对应矩阵的每个元素（矩阵元素从0开始标序号）

#include<bits/stdc++.h>
using namespace std;
using PII = pair<int,int>;

char g[5][5],backup[5][5];
int cnt = 100;
vector<PII> ans;

void turn(int x, int y)
{
    for(int i = 0; i < 4; i++ )
    {
        g[x][i] = g[x][i] != '+' ? '+' : '-';
        g[i][y] = g[i][y] != '+' ? '+' : '-';
    }
    
    g[x][y] = g[x][y] != '+' ? '+' : '-';
}


int get(int x, int y)
{
    return x*4 + y;
}

int main()
{
    for(int i=0;i<4;i++) cin>>g[i];
    
    memcpy(backup, g, sizeof g);
    
    for(int op = 0; op < 1 << 16; op++)
    {
        vector<PII> tmp;
        for(int i = 0; i < 4; i++ )
        {
            for(int j = 0; j < 4; j++ )
            {
                if(op >> get(i,j) & 1)
                {
                    tmp.push_back({i,j});
                    turn(i,j);
                }
            }
        }
        
        bool off = false;
        for(int i = 0; i < 4; i++ )
        {
            for(int j = 0; j < 4; j++ )
            {
                if(g[i][j] == '+')
                {
                    off = true;
                    break;
                }
            }
        }
        
        if(!off && cnt > tmp.size())
        {
            cnt = tmp.size();
            ans = tmp;
        }
        
        memcpy(g, backup, sizeof g);
    }
    
    
    cout << cnt << endl;
    for(auto& op : ans) cout << op.first + 1 << " " << op.second + 1 <<endl;
    return 0;
}

7、费解的开关

你玩过“拉灯”游戏吗？

25 盏灯排成一个 5×5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

我们用数字 1 表示一盏开着的灯，用数字 0 表示关着的灯。

下面这种状态

10111
01101
10111
10000
11011

在改变了最左上角的灯的状态后将变成：

01111
11101
10111
10000
11011

再改变它正中间的灯后状态将变成：

01111
11001
11001
10100
11011

给定一些游戏的初始状态，编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。

输入格式

第一行输入正整数 n，代表数据中共有 n 个待解决的游戏初始状态。

以下若干行数据分为 n 组，每组数据有 5 行，每行 5 个字符。

每组数据描述了一个游戏的初始状态。

各组数据间用一个空行分隔。

输出格式

一共输出 n 行数据，每行有一个小于等于 6 的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。

对于某一个游戏初始状态，若 6 步以内无法使所有灯变亮，则输出 −1。

数据范围

0<<𝑛≤500

输入样例：

3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111

输出样例：

3
2
-1

要使灯泡全亮，25个格子的开关矩阵，每一个开关有开或关两种状态，一共有 2^25 种对矩阵的操作方案，再加上要检测的矩阵数n最高有500个，故暴力枚举所有方案再判断是否满足的方法会超时

通过推演我们发现，一个灯是否改变状态，是由它周围上下左右相邻的开关和它本身的开关决定的，和其他开关并无联系；

如果我们能先确定第一行灯的状态，那么第一行的灯状态的切换只能由第二行的开关决定！

那么如何确定第一行灯的状态呢？

就使用数据给出的第一行的状态去递推后面几行开关的操作可行吗？ 这样做最终的操作次数可能不是最小的；

我们可以枚举对第一行的所有开关的操作，共有2^5种操作方案，每一种操作方案对应了一种第一行的泡的亮暗，再去根据上一行操作后续几行开关；最后只需判断最后一行是否全亮即可（因为通过递推的操作前面几行，已经保证了前四行是全亮的）

这种方法，通过枚举第一行所有情况和题目特定的递推关系，枚举2^5就相当于枚举了2^25(通过递推关系过滤了2^25中很多不可能全亮的情况），因为每当第一行确定后，后续的开关操作都是对应的一种情况

代码：

#include<bits/stdc++.h>
using namespace std;
 
const int N = 30;
char g[N][N],backup[N][N];
int dx[5] = {-1, 0, 1, 0, 0};
int dy[5] = { 0, 1, 0,-1, 0};

void turn(int x, int y)
{
    for(int i = 0; i < 5; i++ )
    {
        int a = x + dx[i];
        int b = y + dy[i];
        if(a < 0 || a >=5 || b < 0 || b >= 5) continue;
        g[a][b] ^= 1; //通过对字符'0' '1'异或 1，可直接切换字符0/1
    }
}

int  solve()
{
    int res = 10;
    for(int i=0;i<5;i++) cin>>g[i];
    
    //备份矩阵g，枚举每次操作后还原，以便下一次枚举
    memcpy(backup, g, sizeof g);
    
    for(int op = 0; op < 32; op++ )//对第一行用二进制枚举，用int存储枚举结果
    {
        int step = 0;
        
        for(int i = 0; i < 5; i++ )
        {
            if(op >> i & 1) //通过右移 + 按位与的方式判断对每一个开关的操作
            {
                step++;
                turn(0, i);
            }
        }
        
        for(int i = 0; i < 4; i++ )
        {
            for(int j = 0; j < 5; j++ )
            {
                if(g[i][j] == '0')
                {
                    step++;
                    turn(i+1,j);
                }
            }
        }
        
        bool dark = false;
        for(int i = 0; i < 5; i++ )
        {
            if(g[4][i] == '0')
            {
                dark = true;
                break;
            }
        }
        
        if(!dark) res = min(res,step);
        memcpy(g,backup,sizeof backup);
    }
    
    if(res > 6) return -1;
    else return res;
}

int main()
{
    int T;
    cin>>T;
    
    while(T--)
    {
        cout << solve() << endl;
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1647820.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Gaea+UE5】创建基本的大型世界场景

【Gaea+UE5】创建基本的大型世界场景

目录 效果 步骤 一、在Gaea中生成地形 二、确定导出的地形规模 三、在UE中创建地形 四、验证UE创建的地形规模是否正确 五、使用M4自动地形材质 效果 步骤 一、在Gaea中生成地形 1. 打开Gaea官网下载软件 2. 打开Gaea软件&#xff0c;我们可以选择一个预设的山体 创…
阅读更多...
机器学习——4.案例: 简单线性回归求解

机器学习——4.案例: 简单线性回归求解

案例目的 寻找一个良好的函数表达式,该函数表达式能够很好的描述上面数据点的分布&#xff0c;即对上面数据点进行拟合。 求解逻辑步骤 使用Sklearn生成数据集定义线性模型定义损失函数定义优化器定义模型训练方法&#xff08;正向传播、计算损失、反向传播、梯度清空&#…
阅读更多...
Implicit Diffusion Models for Continuous Super-Resolution

Implicit Diffusion Models for Continuous Super-Resolution

CVPR2023https://github.com/Ree1s/IDM问题引入&#xff1a; – LIIF方法可以实现任意分辨率的输出&#xff0c;但是因为是regression-based方法&#xff0c;所以得到的结果缺少细节&#xff0c;而生成的方法(gan-based,flow-based&#xff0c;diffusion-based等)可以生成细节&…
阅读更多...
JavaScript中的RegExp和Cookie

JavaScript中的RegExp和Cookie

个人主页&#xff1a;学习前端的小z 个人专栏&#xff1a;JavaScript 精粹 本专栏旨在分享记录每日学习的前端知识和学习笔记的归纳总结&#xff0c;欢迎大家在评论区交流讨论&#xff01; 文章目录 &#x1f506;RegExp &#x1f3b2; 1 什么是正则表达式 &#x1f3b2;2 创建…
阅读更多...
从招标到合作：如何筛选与企业需求匹配的6sigma咨询公司

从招标到合作：如何筛选与企业需求匹配的6sigma咨询公司

在市场竞争激烈的环境中&#xff0c;领军企业需要不断改进和创新才能在行业中保持竞争优势。为了解决产品质量、生产流程和客户满意度等方面的挑战&#xff0c;许多企业选择与6sigma咨询公司合作&#xff0c;推动企业的全面变革和持续发展。下面是企业在选择合作伙伴时通常会经…
阅读更多...
一、Redis五种常用数据类型

一、Redis五种常用数据类型

Redis优势&#xff1a; 1、性能高—基于内存实现数据的存储 2、丰富的数据类型 5种常用&#xff0c;3种高级 3、原子—redis的所有单个操作都是原子性&#xff0c;即要么成功&#xff0c;要么失败。其多个操作也支持采用事务的方式实现原子性。 Redis特点&#xff1a; 1、支持…
阅读更多...
Golang日志实战教程：掌握log与syslog库的高效使用

Golang日志实战教程：掌握log与syslog库的高效使用

Golang日志实战教程&#xff1a;掌握log与syslog库的高效使用 简介理解 Golang 的 log 库基本概念创建日志记录器自定义日志记录器日志级别 深入 syslogsyslog 的基础配置和使用 syslog高级应用 日志格式化与管理日志格式化日志文件管理 日志的高级应用集成第三方日志框架使用 …
阅读更多...
Python程序中温度更新出现振荡问题的分析和解决方案

Python程序中温度更新出现振荡问题的分析和解决方案

在处理温度更新出现振荡问题时&#xff0c;可以考虑以下分析和解决方案&#xff1a;检查温度更新算法是否正确&#xff0c;可能存在错误导致振荡。检查温度更新的步长&#xff08;时间步长&#xff09;是否合适&#xff0c;步长过大可能导致振荡。检查系统动力学模型是否准确&a…
阅读更多...
场外个股期权和场内个股期权的优缺点是什么？

场外个股期权和场内个股期权的优缺点是什么？

场外个股期权和场内个股期权的优缺点 场外个股期权是指在沪深交易所之外交易的个股期权&#xff0c;其本质是一种金融衍生品&#xff0c;允许投资者在股票交易场所外以特定价格买进或卖出证券。场内个股期权是以单只股票作为标的资产的期权合约&#xff0c;其内在价值是基于标…
阅读更多...
如何用Kimi，5秒1步生成流程图

如何用Kimi，5秒1步生成流程图

引言 在当前快节奏的工作环境中&#xff0c;拥有快速、专业且高效的工具不可或缺。 Kimi不仅能在5秒内生成专业的流程图&#xff08;kimi&#xff09;&#xff0c;还允许实时编辑和预览&#xff0c;大幅简化了传统流程图的制作过程。 这种迅速的生成能力和高度的可定制性使得…
阅读更多...
员工账号生命周期如何“全场景”自动化管理？

员工账号生命周期如何“全场景”自动化管理？

当企业在信息化建设中引入越来越多的业务系统时&#xff0c;必然存在系统内账号互相独立、无法打通的情况。一有人事变动&#xff0c;HR、IT 管理员、应用管理员、业务部门主管等人就需要在系统里手动更新账号状态。重复、低效&#xff0c;且不可避免出现安全隐患。困扰着 IT 管…
阅读更多...
冯喜运：5.7全球紧张局势中，黄金原油投资者转向需谨慎

冯喜运：5.7全球紧张局势中，黄金原油投资者转向需谨慎

【黄金消息面分析】&#xff1a;周一&#xff08;5月6日&#xff09;&#xff0c;现货黄金触底回升&#xff0c;盘中交投于2320美元附近。自美国4月非农就业数据出炉和美联储主席鲍威尔货币政策新闻发布会以后&#xff0c;现货黄金从4月12日的历史高点2431美元下跌了大约6.3%&a…
阅读更多...
AI口语对话训练有哪些软件？推荐这5款，简单易用

AI口语对话训练有哪些软件？推荐这5款，简单易用

AI口语对话训练有哪些软件&#xff1f;AI口语对话训练软件在近年来得到了飞速的发展&#xff0c;为语言学习者提供了更为便捷、高效的学习方式。它们借助先进的自然语言处理技术和机器学习算法&#xff0c;不仅模拟了真实对话场景&#xff0c;还提供了个性化的学习建议和即时反…
阅读更多...
笔试强训Day15 二分 图论

笔试强训Day15 二分 图论

平方数 题目链接&#xff1a;平方数 (nowcoder.com) 思路&#xff1a;水题直接过。 AC code&#xff1a; #include<iostream> #include<cmath> using namespace std; int main() {long long int n; cin >> n;long long int a sqrtl(n);long long int b …
阅读更多...
苏州金龙荣获首届无人扫地机器人演示比赛“竞技领跑奖”

苏州金龙荣获首届无人扫地机器人演示比赛“竞技领跑奖”

4月30日&#xff0c;2024年苏州市首届无人扫地机器人演示比赛在高新区思益街展开比拼。五家企业参赛在道路上实地比拼无人扫地机器人技术&#xff0c;通过清扫垃圾、识别路障等环节展现城市清洁的“未来场景”。经过角逐&#xff0c;苏州金龙的无人驾驶清扫车获得步道演示比赛“…
阅读更多...
送给正在入行的小白：最全最有用的网络安全学习路线已经安排上了

送给正在入行的小白：最全最有用的网络安全学习路线已经安排上了

在这个圈子技术门类中&#xff0c;工作岗位主要有以下三个方向&#xff1a; 安全研发安全研究&#xff1a;二进制方向安全研究&#xff1a;网络渗透方向 下面逐一说明一下。 第一个方向&#xff1a;安全研发 你可以把网络安全理解成电商行业、教育行业等其他行业一样&#xf…
阅读更多...
centos7.9系统rabbitmq3.8.5升级为3.8.35版本

centos7.9系统rabbitmq3.8.5升级为3.8.35版本

说明 本文仅适用rabbitmq为RPM安装方式。 升级准备 查看环境当前版本&#xff1a; # cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core) # rabbitmqctl status Status of node rabbitmq01 ... RuntimeOS PID: 19333 OS: Linux Uptime (seconds): 58 Is under …
阅读更多...
Ollama +Docker+OpenWebUI

Ollama +Docker+OpenWebUI

1 Ollama 1.1 下载Ollama https://ollama.com/download 1.2 运行llama3 $ ollama run llama3 pulling manifest pulling 00e1317cbf74... 100% ▕███████████████████████████████████████████████████████████…
阅读更多...
Java 运行的底层原理

Java 运行的底层原理

Java是一种跨平台的编程语言&#xff0c;其底层原理涉及到了多个方面&#xff0c;包括Java虚拟机&#xff08;JVM&#xff09;、字节码、类加载机制、垃圾回收器等。让我们逐一深入了解Java运行的底层原理。 1. Java虚拟机&#xff08;JVM&#xff09; Java虚拟机是Java程序运…
阅读更多...
【前端】HTML基础（1）

【前端】HTML基础（1）

文章目录 前言一、什么是前端二、HTML基础1、 HTML结构1.1 什么是HTML页面1.2 认识HTML标签1.3 HTML文件基本结构1.3 标签层次结构1.4 创建html文件1.5 快速生成代码框架 三、Emmet快捷键 前言 这篇博客仅仅是对HTML的基本结构进行了一些说明&#xff0c;关于HTML的更多讲解以及…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023