题目一:不同路径的数目(一)
题目描述:
一个机器人在m×n大小的地图的左上角(起点)。机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。可以有多少种不同的路径从起点走到终点?
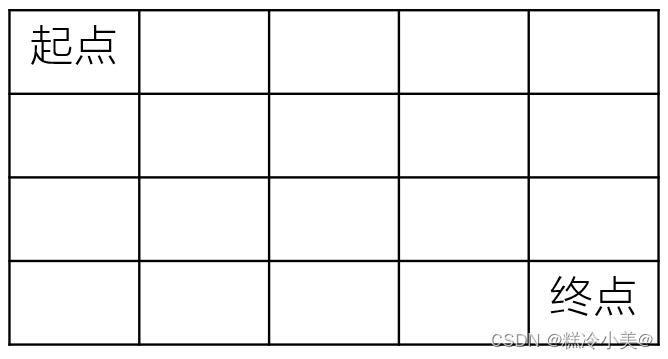
输入输出描述:
输入:2,2 返回值:2
题目解析:
- step 1:用
dp[i][j]表示大小为i∗j的矩阵的路径数量,下标从0开始。 - step 2:(初始条件) 当i或者j为0的时候,代表矩阵只有一行或者一列,因此只有一种路径。
- step 3:(转移方程) 每个格子的路径数只会来自它左边的格子数和上边的格子数,因此状态转移为dp[i][j]=dp[i−1][j]+dp[i][j−1]。
作答情况:
属于简单题,正确。
代码:
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param m int整型
* @param n int整型
* @return int整型
*/
public int uniquePaths (int m, int n) {
int[][] dp=new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0||j==0) {
dp[i][j]=1;
}else{
dp[i][j]=dp[i][j-1]+dp[i-1][j];
}
}
}
return dp[m-1][n-1];
}
}题目二:短距离最小路径和
题目描述:
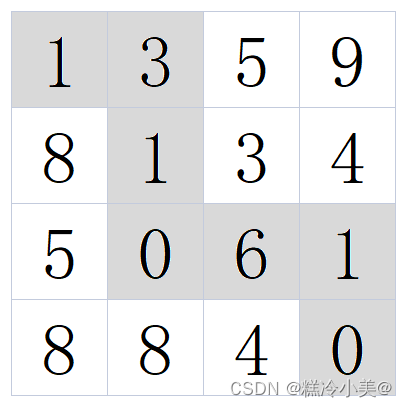
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
输入输出描述:
输入:[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]] 返回值:12
说明:
题目解析:
- step 1:我们可以构造一个与矩阵同样大小的二维辅助数组,其中dp[i][j]表示以(i,j)位置为终点的最短路径和。
- step2:判断特殊情况:二维数组只有一个值时,dp[0][0]=matrix[0][0]。
- step 3:很容易知道第一行与第一列,只能分别向右或向下,没有第二种选择,因此第一行只能由其左边的累加,第一列只能由其上面的累加。
- step4:只有一行或一列时,只能向右或向下走过来,(一行) dp[0][j]=matrix[0][j]+dp[0][j-1];
(一列) dp[i][0]=matrix[i][0]+dp[i-1][0]; - step 5:边缘状态构造好以后,遍历矩阵,补全矩阵中每个位置的dp数组值:因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]。
- step 4:最后移动到(n−1,m−1)的位置就是到右下角的最短路径和。
作答情况:
没有判断一行或一列情况下的特殊情况。
代码:
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param matrix int整型二维数组 the matrix
* @return int整型
*/
public int minPathSum (int[][] matrix) {
int m=matrix.length;
int n=matrix[0].length;
int[][] dp=new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
//终点即起点
if(i==0&&j==0) dp[i][j]= matrix[i][j];
//只有一行
else if(i==0) dp[i][j]=matrix[i][j]+dp[i][j-1];
//只有一列
else if(j==0) dp[i][j]=matrix[i][j]+dp[i-1][j];
//多行多列下任意位置,前一个只能向下或向右来到达
else dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+matrix[i][j];
}
}
//移动到右下角
return dp[m-1][n-1];
}
}题目三:把数字翻译成字符串
题目描述:
有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。现在给一串数字,返回有多少种可能的译码结果。
输入输出描述:
输入:"12" 返回值:2
说明:2种可能的译码结果(”ab” 或”l”)
输入:"31717126241541717" 返回值:192
题目解析:
1.用辅助数组dp表示前i个数的译码方法有多少种。
2.数字为单数:数字非零(1种),数字为零(0种)
3.数字为多位数:
3.1 数字种存在0:数字中有10和20(两位数:1种,多位数:dp[i]=dp[i-2]种)
数字不是10和20(0种)
3.2 数字中没有0:数字范围为11~19 21~26 (两位数:2种,多位数:dp[i]=dp[i-2]+dp[i-1]种)
数字范围大于26(两位数和多位数都是dp[i]=dp[i-1])
作答情况:
数字种存在0:数字中有10和20 没有判断两位数和多位数情况。
代码:
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 解码
* @param nums string字符串 数字串
* @return int整型
*/
public int solve (String nums) {
int m=nums.length();
//dp[i]:到了i位置上把数字翻译成字符串的方式有几种
int[] dp=new int[m];
//(数字是单数)
if(nums.charAt(0)!='0') dp[0]=1;
else dp[0]=0;
//(数字是多位数)从第二位开始遍历
for(int i=1;i<dp.length;i++){
//尾位置存在0
if(nums.charAt(i)=='0'){
//0前面是1或2开头
if(nums.charAt(i-1)=='1'||nums.charAt(i-1)=='2'){
//数字是两位
if(i==1) dp[i]=1;
//数字是多位
else dp[i]=dp[i-2];
}
// //0前面不是1或2开头
else{
dp[i]=0;
}
}
//尾位置不存在0
else {
if((nums.charAt(i-1)=='1'&&nums.charAt(i)<='9')||(nums.charAt(i-1)=='2'&&nums.charAt(i)<='6')){
//两位
if(i==1) dp[i]=2;
// 多位
else
dp[i]=dp[i-1]+dp[i-2];
}
else dp[i]=dp[i-1];
}
}
return dp[m-1];
}
}