算法原理

通过题目的第二条我们可以知道：这道题只有两种结果：
（1）一直循环并且变不成1；
（2）能变成1

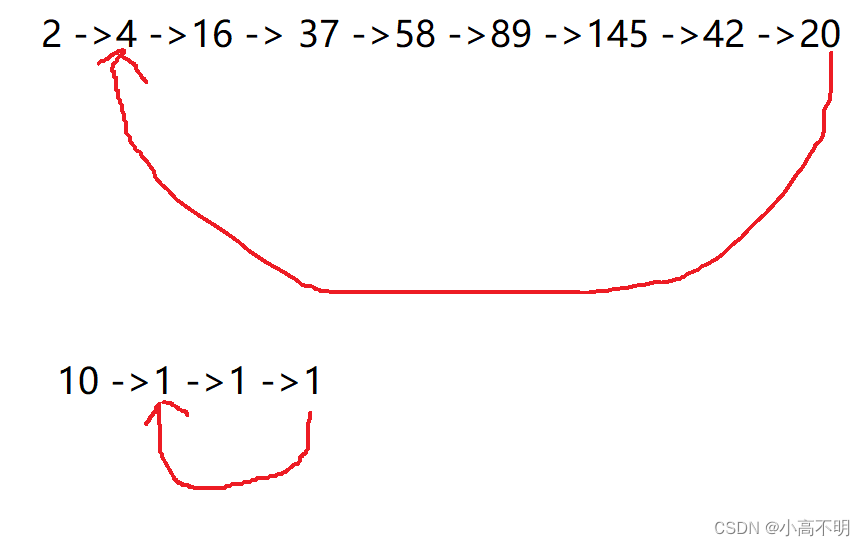
以上的两种情况其实我们可以归结成一种情况：都是无限循环但是第二种是对于1的无限循环。
因此我们可以使用快慢指针法：使用这个方法有一个好处就是：当没有环的时候快慢指针一定不会相遇，有环的时候才会相遇，这样也符合我们的分析。当快慢指针相遇的时候我们只需要判断相遇的点是否是1就行了。

趣味拓展

上述两种情况是题目告诉我们的，但是假如没有了第二条题目，这道题的复杂的度就直接上来了，因为我们要考虑是否有那种无限循环且不重复的情况。此时我们可以由一个定理来证明一下：雀巢定理。
雀巢定理的内容：有 n 个巣 ，有n + 1个鸽子，如果让所有鸽子都归巢，那至少有一个巣里面的鸽子的数量大于1。

代码实现：

class Solution {
    public int bitSqrt(int n ){
        int sum = 0,tmp;
        while( n !=0 ){
            tmp = n%10;
            sum+=tmp*tmp;
            n/=10;
        }
        return sum;
    }
    public boolean isHappy(int n) {
        int slow = n,fast = bitSqrt(n);
        while( slow != fast){
            //下面的操作就是保证快指针移动两位，慢指针移动一位
            slow = bitSqrt(slow);
            fast = bitSqrt(bitSqrt(fast));
        }
        return slow == 1;
    }
}

通过上面代码我们可以了解到，其实双指针只是一种思想，它可以是下标，也能是具体的数字（如上所示）。