[leetcode] 63. 不同路径 II

news2025/10/31 11:52:11

文章目录

题目描述
解题方法
- 动态规划
- - java代码
  - 复杂度分析
相似题目

题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：
在这里插入图片描述

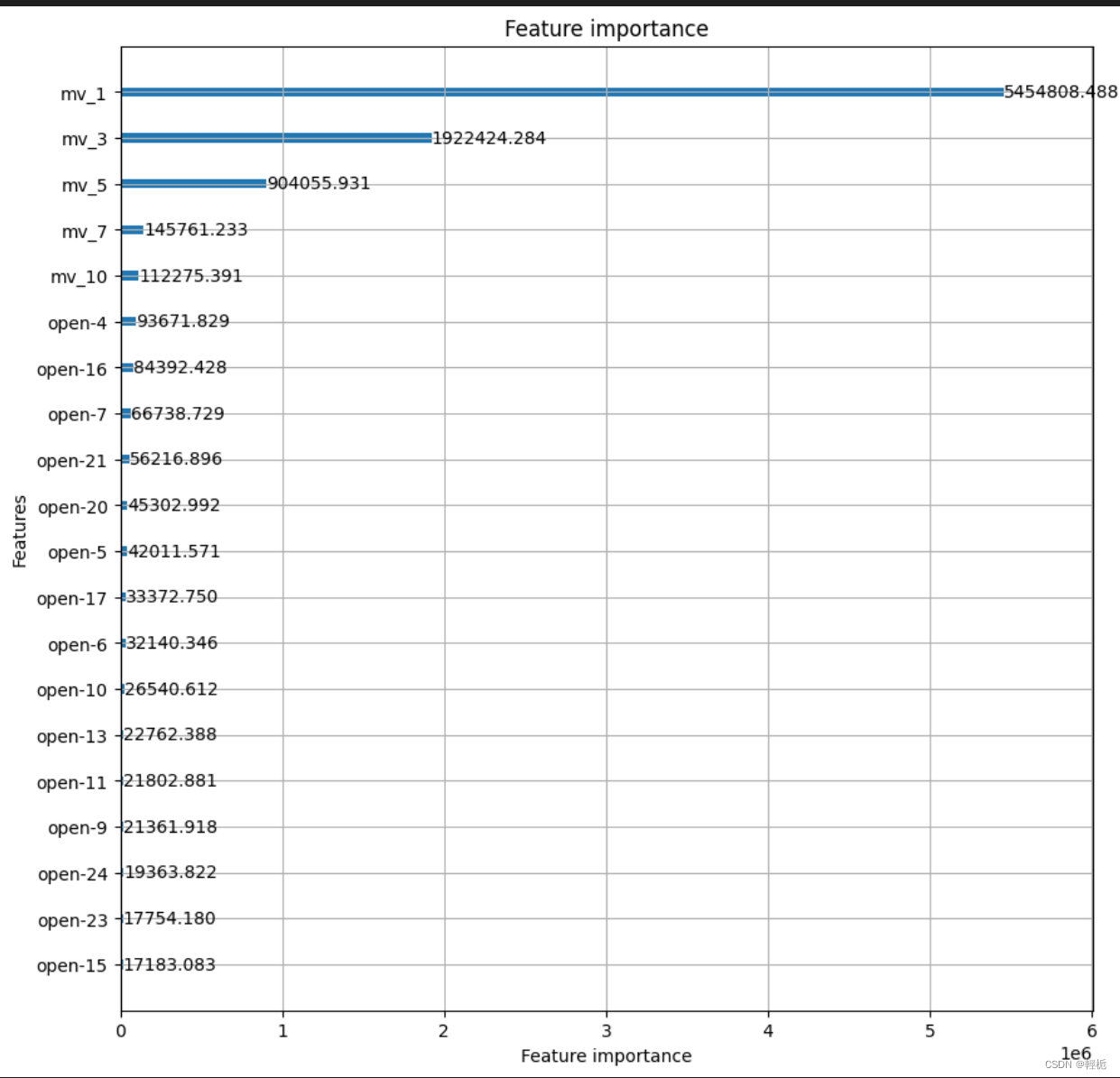
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：
在这里插入图片描述

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

解题方法

动态规划

这道题和第62题相似，只不过多了障碍物。我来总结下规律。

我们设 $f (i, j)$ 为机器人从左上角走到 $(i, j)$ 的路径数量，若机器人在 $(i, j)$ 处，则机器人上一步的位置在 $(i - 1, j)$ 或者 $(i, j - 1)$ 处，由此可推出

当 $i > 0$ 且 $j > 0$ 时，若 $o b s t a c l e G r i d [i] [j] = 0$ ，则 $f (i, j) = f (i - 1, j) + f (i, j - 1)$ ；若 $o b s t a c l e G r i d [i] [j] = 1$ ，则 $f (i, j) = 0$ 。
当 $i = 0$ 或 $j = 0$ 时，若 $(i, j)$ 处有障碍物或在障碍物后面，则 $f (i, j) = 0$ ；否则， $f (i, j) = 1$ 。

java代码

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length;
    int n = obstacleGrid[0].length;
    int[][] dp = new int[m][n];

    for (int i = 0; i < m; i++) {
        if (obstacleGrid[i][0] == 0) {
            dp[i][0] = 1;
        } else {
            break;
        }
    }

    for (int i = 0; i < n; i++) {
        if (obstacleGrid[0][i] == 0) {
            dp[0][i] = 1;
        } else {
            break;
        }
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[i][j] == 0) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    return dp[m - 1][n - 1];
}