Problem: 295. 数据流的中位数

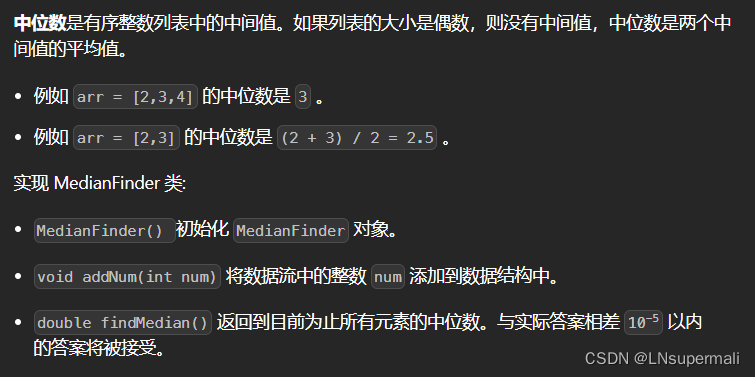
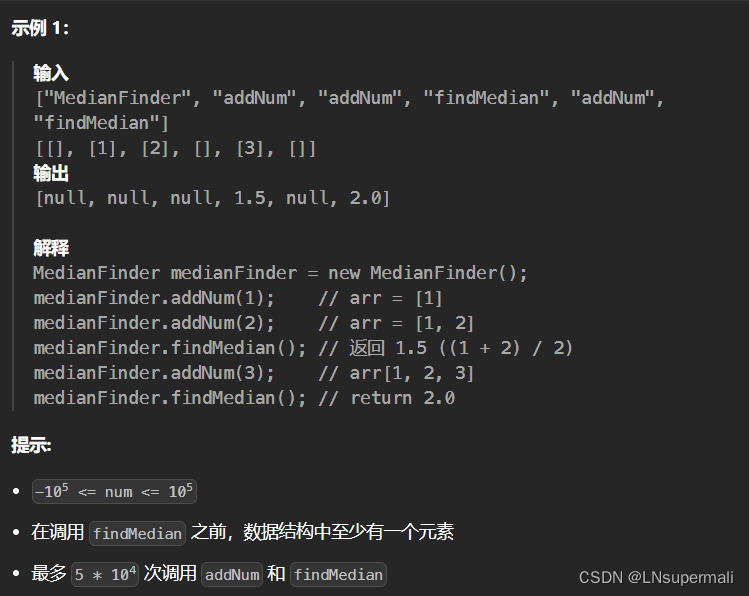
题目描述

思路

1.定义一个大顶堆和小顶堆；
2.当添加的数据小于大顶堆的堆顶元素或者大顶堆为空时，将元素添加到大顶堆；当元素大于大顶堆堆顶元素时添加到小顶堆；同时维护大小顶堆，当大顶堆的元素个数小于小顶堆时，将小顶堆多出大顶堆个数的堆顶元素拿出添加到大顶堆；当小顶堆元素小于大顶堆元素个数减1时将大顶堆多出的堆顶元素添加到小顶堆；
3.当大小顶堆的元素个数一样时，取各自的堆顶元素相加除以2；否则取出大顶堆的堆顶元素；

复杂度

时间复杂度:

$O(logn)$;其中$n$为数据数据流的数据个数

空间复杂度:

$O(n)$

Code

class MedianFinder {
    /* Maintain a large top heap and a small top heap */
    private PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });

    private PriorityQueue<Integer> minHeap = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    });

    public MedianFinder() {

    }

    /**
     * Data flow inserts data
     *
     * @param num Data to be inserted
     */
    public void addNum(int num) {
        if (maxHeap.isEmpty() || num <= maxHeap.peek()) {
            maxHeap.add(num);
        } else {
            minHeap.add(num);
        }
        /**
         Maintain the number relationship between two heaps
         1. The number of elements in the large top heap is not less than that in the small top heap
         2. The number of small top heap elements can be less than the number of large top heap elements minus 1
         */
        while (maxHeap.size() < minHeap.size()) {
            Integer temp = minHeap.poll();
            maxHeap.add(temp);
        }
        while (minHeap.size() < maxHeap.size() - 1) {
            Integer temp = maxHeap.poll();
            minHeap.add(temp);
        }
    }

    /**
     * Find the median
     *
     * @return double
     */
    public double findMedian() {
        if (maxHeap.size() == minHeap.size()) {
            return (minHeap.peek() + maxHeap.peek()) / 2f;
        } else {
            return maxHeap.peek();
        }
    }
}