使用C语言实现杨氏矩阵并找出数字

news2024/12/23 22:58:45

前言

过了五一假期，咋们经过了一个假期的休息，要继续学习了，不能偷懒哦！！

今天让我们来看看如何在一个杨氏矩阵中找出自己想找到的数字。

首先，我们要了解一下杨氏矩阵到底是什么，如果一个矩阵中的每行元素从左到右，从上到下都是递增的，并且它的行和列的长度也是递增的，那么我们可以称这个矩阵为杨氏矩阵。

来让我们看看今天的题目

题目描述

有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。

要求：时间复杂度小于O(N);

输入描述：

无

输出描述：

一行，

题目解析

我们之前已经了解了杨氏矩阵的概念，在这道题中，其实就是让我们在杨氏矩阵中找到一个数字，但是还有一个要求，是时间复杂度小于O(N)，这是什么意思呢？

时间复杂度解释

我们把这个杨氏矩阵看作一个二维数组，如果这个数组中有n个元素，你去遍历数组，去找你想要找的那个元素的话，最坏的情况是找n次，如果我们去遍历，我们就叫它的时间复杂度为O(N)，时间复杂度讨论的是这个算法最坏的情况下的一个数量级。

不知道这样说大家能不能理解，这个时间复杂度小于O(N)其实就是告诉我们，不能通过遍历这个数组的方式去找到我们想要找的数字，遍历这个数组的时候时间复杂度是等于O(N)的，我们要去观察杨氏矩阵的规律，使用自己的方式解决问题。

杨氏矩阵图解

我们就画一个简单的杨氏矩阵来观察一下它的特点吧

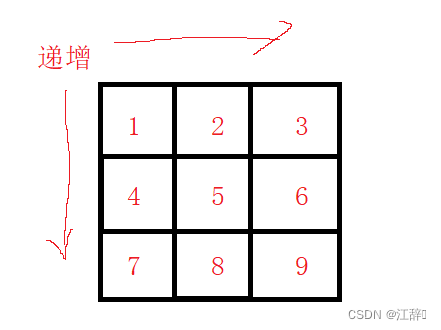
我们发现，在这个杨氏矩阵中，根据杨氏矩阵的特点来看，它又上角的数字是一行里面最大的，又是一列里面最小的，我们可以使用这个特征去写代码。

基本逻辑

当我们要去找7这个数字的时候，我们拿3与他比较，发现7比3大，那么3已经是第一行里最大的元素了，我们就可以将第一行排除出去，在其他的元素中找我们要找的数字

当我们要去找2这个数字的时候，我们还是拿3与他比较，我们发现2比3小，那么这个时候3已经是他自己那一列最小的元素了，这一列就不可能有我们要找的元素，所以可以将有3的这一列给排除，在其他的元素中找我们要找的数字。

基本逻辑我们清楚了，上代码

代码展示

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void find_k(int arr[3][3], int r, int c, int k)
{
	int x = 0;
	int y = c - 1;
	int flag = 0;//假设找不到元素
	//当行x下标小于等于2的时候，列元素下标大于等于0的时候进入循环，防止越界
	while (x<=r-1&&y>=0)
	{
		//使用右上角元素与k进行比较，如果右上角元素比k小那么行x+1，在下一行里寻找
		if (arr[x][y] < k)
		{
			x++;
		}
		//右上角元素比k大列减1，排除列
		else if (arr[x][y] > k)
		{
			y--;
		}
		else
		{
			printf("找到了，下标是：%d %d", x, y);
			flag = 1;
			break;
		}
	}
	if (flag == 0)
	{
		printf("找不到\n");
	}
}
int main()
{
	int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };
	int k = 7;
	find_k(arr, 3, 3,k);
}