CNN笔记详解

CNN(卷积神经网络)

计算机视觉，当你们听到这一概念的是否好奇计算机到底是怎样知道这个图片是什么的呢？为此提出了卷积神经网络，通过卷积神经网络，计算机就可以识别出图片中的特征，从而识别出图片中的物体。看到这里充满疑惑了把！接下来我们将依次介绍人工神经网路，CNN（卷积神经网络）并详细介绍卷积层，池化层，全连接层。来教你理解CNN的工作流程。

1. 人工神经网路

1.1 神经元

如下图所示，每个神经元接受线性组合的输入后，最开始只是简单的线性加权，后来给每个神经元加上了非线性的激活函数，从而进行非线性变换后输出。线性变换就是 $y = w_1 * x_1 + b$

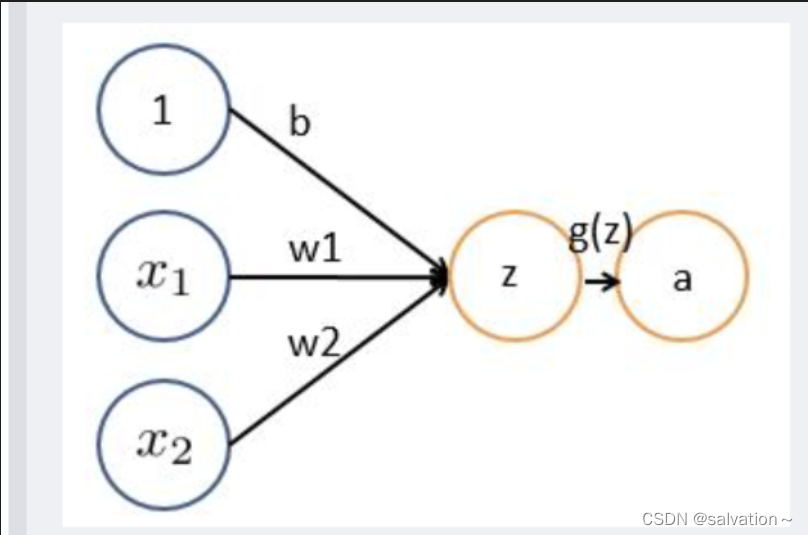
在这里插入图片描述

之前没了解过的人看到这里就很蒙了，为什么一个线性变化就可以得到所需要的特征呢？这里我们举个例子来说明：

明天有一场聚会，你去不去呢？影响的因素有：
聚会内容记为 $x_1$ , $x_1 = 1$ 代表有你喜欢的聚会内容，如果你有5个聚会内容都很喜欢你可以将 $w_1 = 5$ ， $x_1 = 0$ 代表没你喜欢聚会的内容。
聚会参与者记为 $x_2$ , $x_2 = 1$ 代表有你喜欢的白月光，如果有可以将 $w_2 = 100$ , $x_2 = 0$ 代表没有喜欢的人。
最后通过加权求和 $y = w_1 * x_1 + w_2 * x_2 + b$ ,就可以得到你想不想去的结果了。假如你喜欢聚会内容，并且有喜欢的人，那么 $y = 100 + 5 + 10 = 115$ ，b是偏置项，这里理解为为更好达到目的而设置的偏置项，那么你就可以去参加这个聚会了。但是有人会提出疑问了，去不去似乎用概率来描述更合适，所以我们可以对y进行一个非线性变化，也就是增加非线性激活函数来使结果在0到1之间。常见的非线性激活函数有：

sigmoid函数：
$\frac{1}{1 + e^{-x}}$
tanh函数：
$\frac{e^x - e^{-x}}{e^x + e^{-x}}$
ReLU函数：
$y = ma x (0, x)$
Leaky ReLU函数：
$y = ma x (0.01 x, x)$

这里对sigmoid函数进行一个简单的解释：

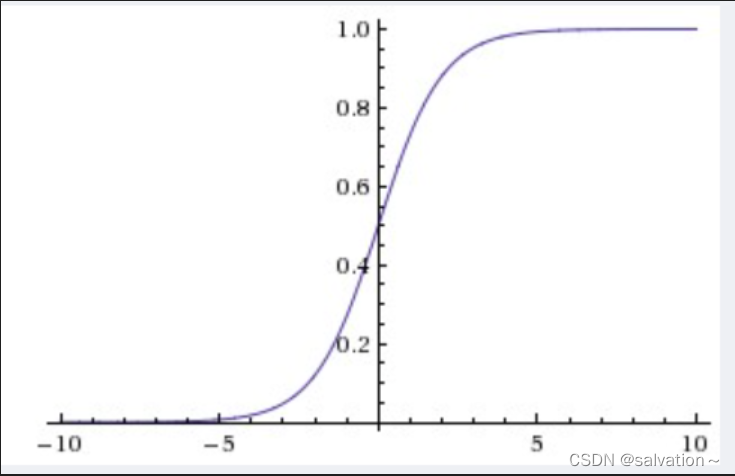
在这里插入图片描述

通过图像我们知道该激活函数将输入映射到0-1之间，可以很好的实现我们的目标。下面我们用代码实现一下：

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

print(sigmoid(115))

1.0

输出结果为1，代表我们特别特别想去这个聚会。

1.2 神经网络

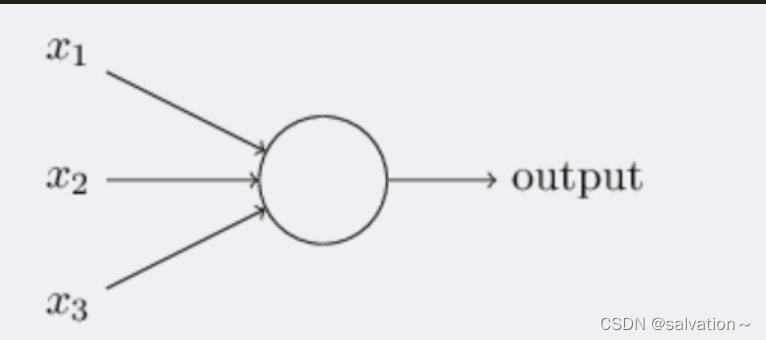
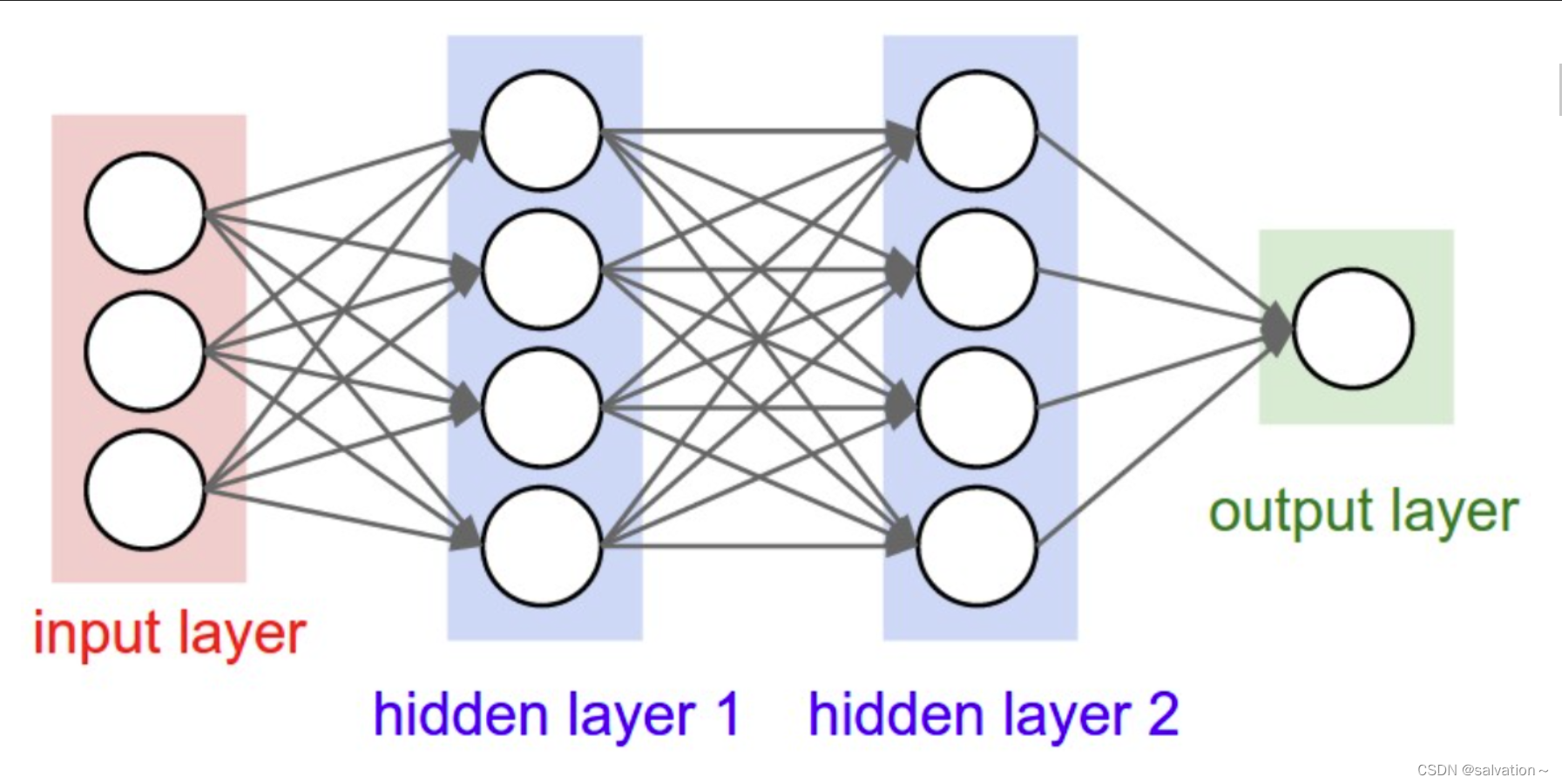
在这里插入图片描述

将多个上图中的神经元连接起来就可以得到下图中的神经网络。

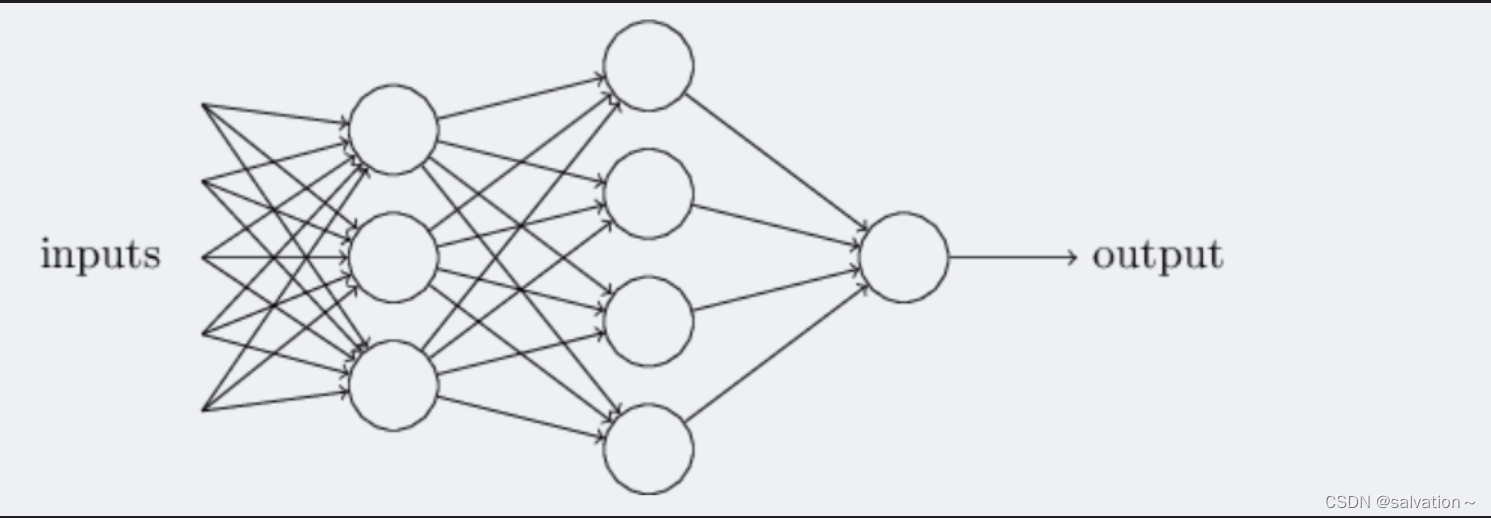
在这里插入图片描述

上图最左边叫做输入层，中间部分叫做隐藏层，最右边叫做输出层。
输入层：你将要喂入的数据，通常用于处理原始数据，如数据归一化，数据输入的形状等
隐藏层：神经网络的计算过程，隐藏层通常用于提取特征，学习输入数据之间的关联和模式。隐藏层的状态(神经元的输出值)通常被认为是模型的知识库。
输出层：神经网络的输出结果，可能包含一个或多个神经元。

在这里插入图片描述

2. CNN（卷积神经网络）

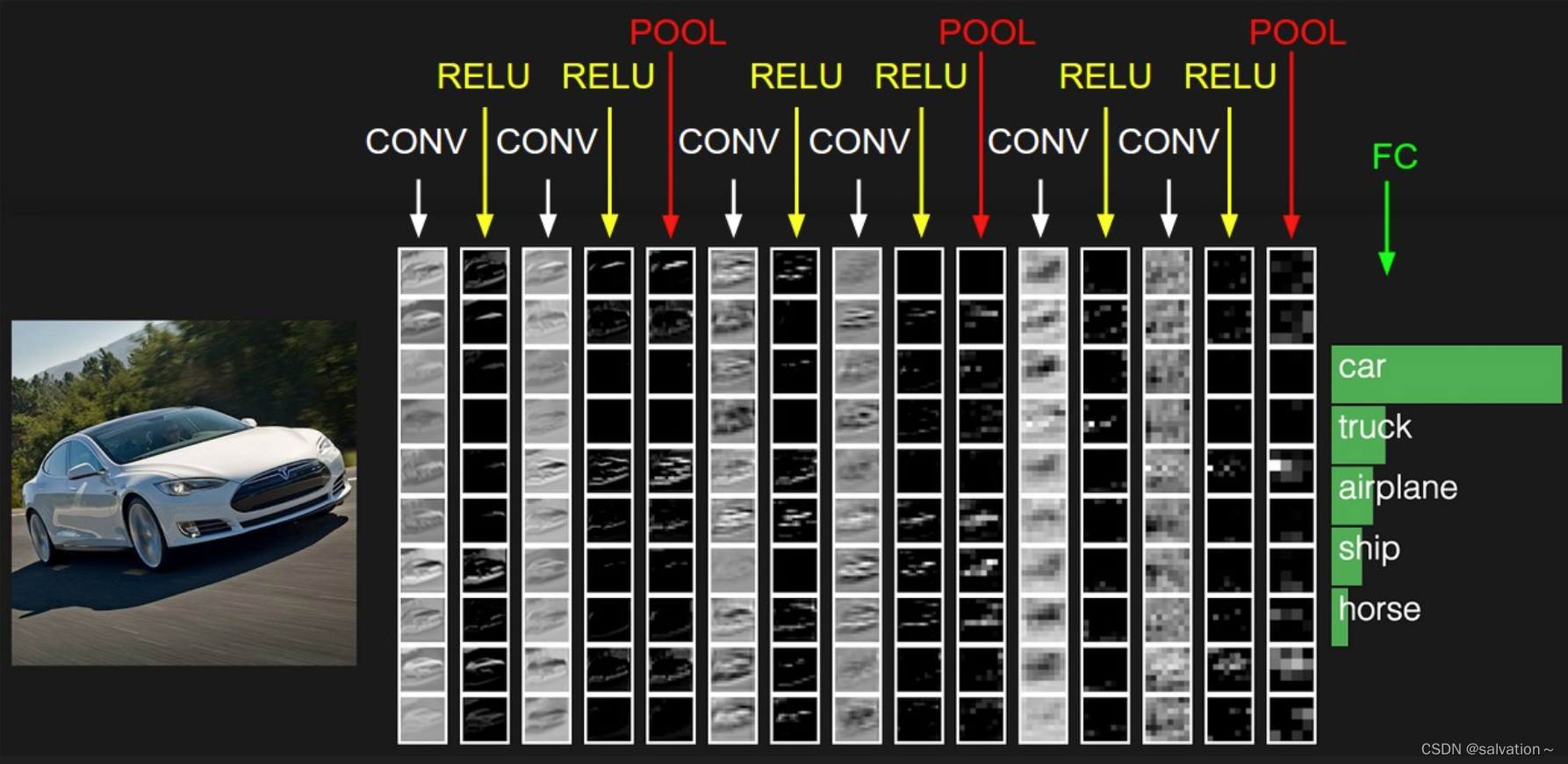
在这里插入图片描述

上图中最左边输入的是一张图片，那么电脑是如何来提取图片特征，来识别出他是马还是车还是人的呢？在我们眼中图片就是图片，但是在计算机中图片就是由一个个像素点组成的，每个像素点都有RGB三个值，分别代表红，绿，蓝。下图中我们将展示一个灰度图像。

在这里插入图片描述

上图又称为灰度图像，因为其每一个像素值的范围是0_{255（由纯黑色到纯白色），表示其颜色强弱程度。另外还有黑白图像，每个像素值要么是0（表示纯黑色），要么是255（表示纯白色）。我们日常生活中最常见的就是RGB图像，有三个通道，分别是红色、绿色、蓝色。每个通道的每个像素值的范围也是0}255，表示其每个像素的颜色强弱。但是我们日常处理的基本都是灰度图像，因为比较好操作（值范围较小，颜色较单一），有些RGB图像在输入给神经网络之前也被转化为灰度图像，也是为了方便计算，否则三个通道的像素一起处理计算量非常大。当然，随着计算机性能的高速发展，现在有些神经网络也可以处理三通道的RGB图像。

# 使用opencv打开图片
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('./image/v2-efd4f4517d5bdb43858a04f7e4ff5f7f_r.jpg')

print(img)

[[[156 172 185]
  [156 172 185]
  [156 172 185]
  ...
  [116 127 141]
  [115 126 140]
  [115 126 140]]

 [[156 172 185]
  [156 172 185]
  [156 172 185]
  ...
  [116 127 141]
  [115 126 140]
  [115 126 140]]

 [[156 172 185]
  [156 172 185]
  [156 172 185]
  ...
  [116 127 141]
  [115 126 140]
  [115 126 140]]

 ...

 [[210 219 232]
  [208 217 230]
  [205 214 227]
  ...
  [173 182 196]
  [173 182 196]
  [170 179 193]]

 [[209 218 231]
  [208 217 230]
  [207 216 229]
  ...
  [174 183 197]
  [172 181 195]
  [170 179 193]]

 [[209 218 231]
  [209 218 231]
  [208 217 230]
  ...
  [174 183 197]
  [172 181 195]
  [169 178 192]]]

print(img.shape)

(1350, 1080, 3)

img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

plt.axis('off')
plt.imshow(img)

<matplotlib.image.AxesImage at 0x1b06eb1fb50>

在这里插入图片描述

通过上面的代码我们可以知道图片在计算机中是以矩阵来存储的。上述代码只是演示的作用不需要读者理解，如果感兴趣可以去自行学习

那么CNN是怎么进行识别的呢？

计算机中存储了一个正确的图片例如‘X’，然后将输入的图片跟正确的图片进行比较，如果二者一致则判定为‘X’，并且经过旋转、缩放、平移等变换后，计算机也能正确识别出‘X’。因为我们识别的图片不可能跟保存的图片一模一样。

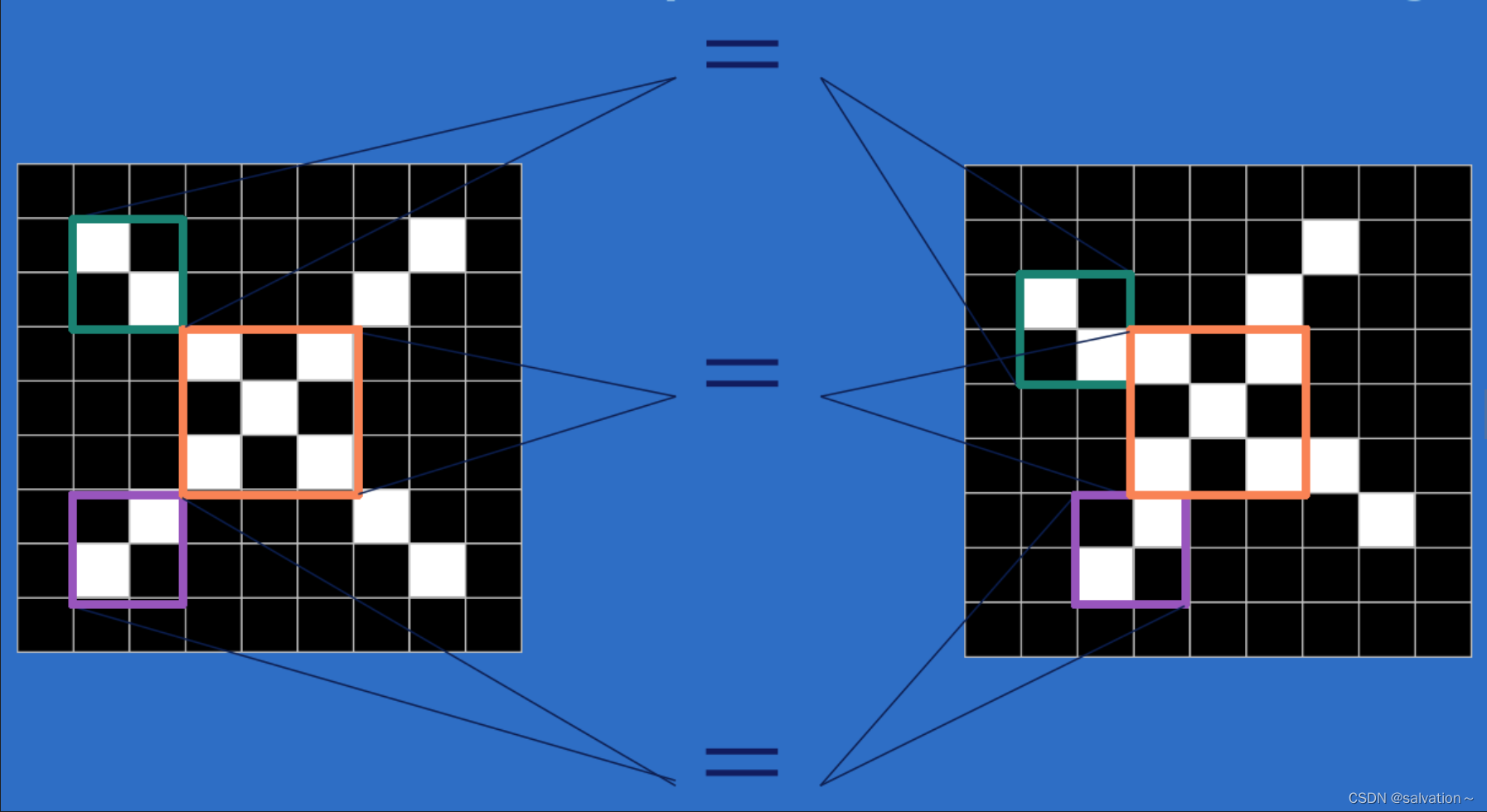
在这里插入图片描述

上图中左右两个图片都是’X‘，但是它们在计算机中存储的矩阵完全不同。假如我们这里黑色为0，baise为1，那么两张图片的矩阵肯定不一样，如果按照像素值一个一个的对比那么计算机会死板的觉得两个是不一样的东西，所以CNN就是用来解决这一问题的。CNN是将两幅图片的一部分进行挨个比较。例如上图中有绿色，紫色，橙色三个小部分，通过对三个小区域的比较来进行判断远远优于对整幅图片进行比较。

看到这里是不是对CNN有点感觉了，下面我们将详细介绍卷积操作。

什么是卷积？

卷积：对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。
这里的滤波矩阵称为卷积核

在这里插入图片描述

卷积核通过在输入图像上不断的移动，每一次移动都进行一次乘积求和，作为此位置的值。上图形象的展示了卷积核的移动过程，通过不断的移动我们可以得到图片每个区域的特征。浅蓝色的部分为输入的原图像，深色为卷积核，不动的绿色为输出的特征值。这完全实现了我们想要的，提取图片每个区域的特征后进行比较。
但是有人就会发现每次卷积核移动的时候中间部分都被计算了，而边缘的只被计算了一次，这样子中间的特征加强了，边缘的特征不就被弱化了（特征丢失），导致结果并不准确。所以为了解决这个问题我们可以在原图像的周围扩展几圈用0进行填充，这样就不会造成特征丢失了。如下图所示。

在这里插入图片描述

下图展示了更复杂的特征提取，我们都知道彩色图片是RGB三通道组成的，下图是用两个卷积核对彩色图片进行特征提取，卷积过程如下所示。最后我们会得到两个特征矩阵。

在这里插入图片描述

卷积整体过程就如下图所示：卷积核在图片上不断移动得到特征值。

在这里插入图片描述

以上就是卷积层的基础知识。感觉还不错把！接下里我们将解释涉及到池化层，和全连接层

3. 池化层

池化：池化层是卷积神经网络中的一种特殊层，用于对输入数据进行降维，减少参数数量，提高网络的泛化能力。池化层通常位于卷积层之后，可以对卷积层的输出进行下采样操作。池化层可以分为最大池化和平均池化两种类型。最大池化是指选择每个池化区域的最大值作为输出，平均池化是指选择每个池化区域的平均值作为输出。池化层可以用于减少特征图的尺寸，同时保持主要特征不变。

在这里插入图片描述

上图展示的就是最大池化，取区域最大值作为输出。

全连接层

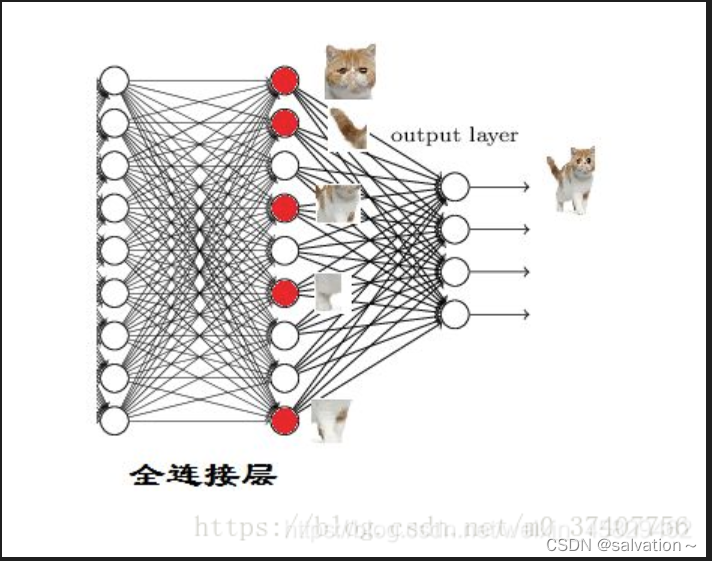
全连接层：就是将之前的卷积层和池化层得到的特征值进行拼接，然后将拼接后的特征值输入到全连接层中，全连接层的作用就是将特征值映射到输出层，从而实现对输入数据的分类。例如我们通过卷积和池化提取到了这个眼睛，嘴巴，鼻子等特征，如果我们利用这些特征来判断是为人还是猫，我们只需要将提取到的所有特征图进行“展平”，将其维度变为1 × x，这个过程就是全连接的过程，也就是说，此步我们将所有的特征都展开并进行运算，最后会得到一个概率值，这个概率值就是输入图片是否是人的概率，这个过程如下所示：

在这里插入图片描述

import torch.nn as nn
import torch.nn.functional as F
import torch

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
        
    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        print(x.shape)
        x = x.view(-1, 16 * 5 * 5)
        print(x.shape)
        x = F.relu(self.fc1(x))
        print(x.shape)
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

net = Net()
print(net)

Net(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
  (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

image = torch.randn(1, 3, 32, 32)
output = net(image)
print(output)

torch.Size([1, 16, 5, 5])
torch.Size([1, 400])
torch.Size([1, 120])
tensor([[-0.1083,  0.0951,  0.0376, -0.0808,  0.0035,  0.0367,  0.0273,  0.1101,
         -0.1449,  0.0607]], grad_fn=<AddmmBackward0>)

通过代码的输出结果我们可以知道，第一个全连接层将[1, 16, 5, 5]展平成了[1, 400]的形状，第二个全连接层展平成了[1, 120]的形状，第三个全连接层展平成了[1, 84]的形状，最后输出层展平成了[1, 10]的形状。这样的输出就可以用来解决10分类问题。

借鉴文章：
CNN

CNN

全连接层