一、LoRA
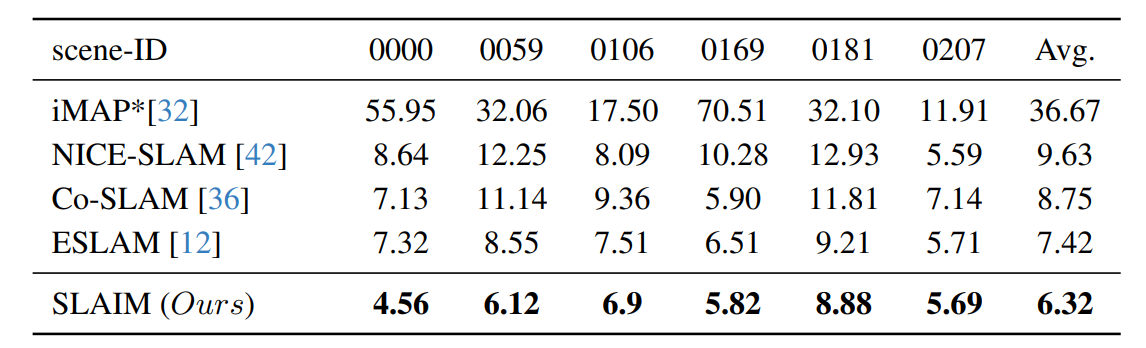
在大语言模型中,参数矩阵 W ∈ R d × d W\in \mathbb{R}^{d \times d} W∈Rd×d的维度往往可以达到百亿甚至千亿,如果从头开始训练将会特别的消耗时间和资源。因此往往大家都会预先训练好一组初始参数 W 0 ∈ R d × d W_0\in \mathbb{R}^{d \times d} W0∈Rd×d,然后针对不同的任务进行微调,即 W = W 0 + Δ W W = W_0+\Delta W W=W0+ΔW。对于微调量,通常假设 Δ W \Delta W ΔW是一个低秩矩阵,即 Δ W = B A \Delta W = BA ΔW=BA, B ∈ R d × r B \in \mathbb{R}^{d \times r} B∈Rd×r, A ∈ R r × d A \in \mathbb{R}^{r \times d} A∈Rr×d, r < < d r << d r<<d,实际结果中也往往能得到很好的效果[2],如图1所示。因此我们针对特定任务只需要重新训练矩阵 B , A B,A B,A即可,它们的维度也远远小于原矩阵 W W W的维度。初始化时设置 A A A是随机生成的矩阵(高斯分布均值为0, 标准差为 σ \sigma σ), B B B为零矩阵可以保证初始微调量 Δ W \Delta W ΔW为0。
而在推理过程中,推理输出
h
=
W
x
h = Wx
h=Wx也可以表示成
h
=
W
0
x
+
B
A
x
.
h = W_0 x + BAx.
h=W0x+BAx.

图1:LoRA算法原理图[1]
下图是截取原文中的部分实验结果。相比于fine-tuning (FT)的方法,LoRA算法只需要很少的训练模型参数就可以得到相似的效果。
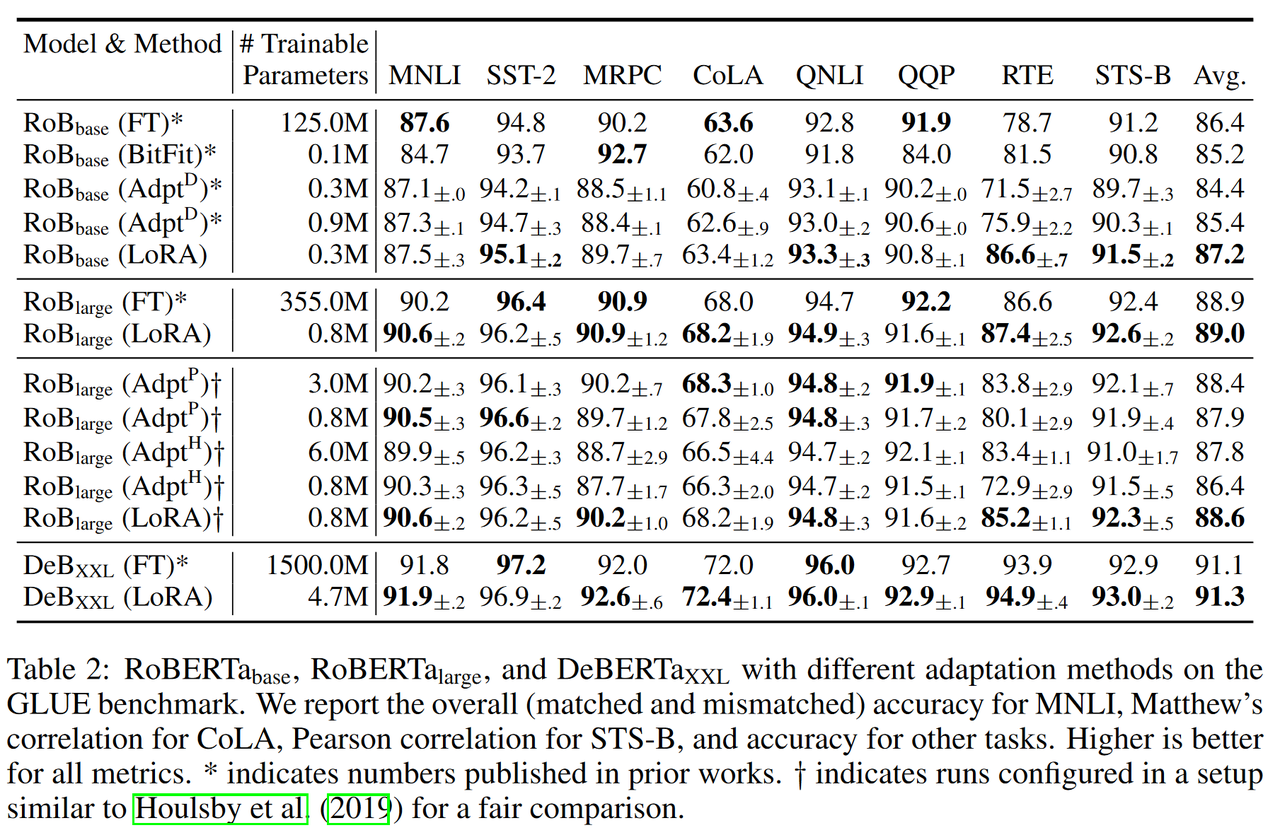
图2:LoRA实验结果[1]
二、LoRA性能加速
2.1 LoRA+
LoRA给两个低秩适配器矩阵 A , B A,B A,B设置了相同的学习率。在LoRA+[3]中,研究人员为适配器矩阵A和B设置不同的学习率,通过对学习率进行精细调整,确保在大模型宽度下,微调过程可以有效地进行特征学习。文中实验说明在相同的计算成本下,LoRA+能获得1% - 2%的性能提高和2倍的计算加速。
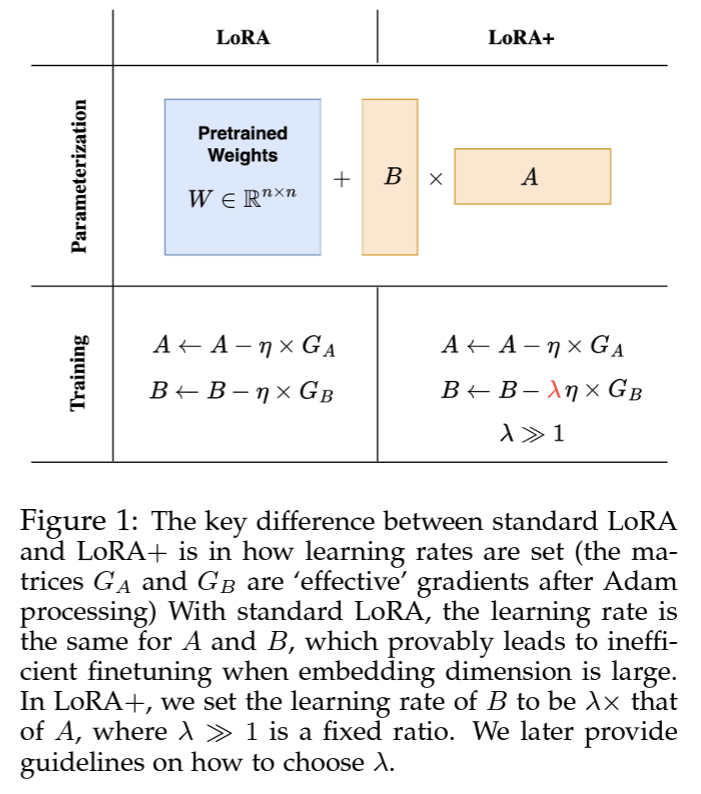
图3:LoRA和LoRA+算法比较[3]
2.2 QLoRA
LoRA成功地减少了所需要的模型的参数个数。除此之外,我们还需要注意模型的实际计算时间(包括训练和推理)也和使用的数据结构有紧密的关系。对于相同的运算,低精度(如FT4)的数据相比于高精度(FT32)的数据花费的时间要少很多。同时,存储高精度数据还需要更多的内存,对于大语言模型而言也是一笔很大的开销。
对于LoRA的计算公式

QLoRA的降精度操作具体如下:

可以看到,高维参数 W W W只使用低精度4 bit的FT4数据类型,只有和梯度有关的参数 L 1 , L 2 L_1,L_2 L1,L2的计算用到相对高精度的BF16数据类型,而 L 1 , L 2 L_1,L_2 L1,L2本身的维度远小于 W W W(低秩假设)。这样数据存储时使用FT4可以大大减少 W W W所需内存,而在需要计算时,我们将需要更新的部分的 W W W(例如1%的参数量)从FT4转化为高精度数据进行计算,这样只需要更新参数时候需要高精度数据,并且参数更新完后又变成低精度数据存储。
关于QLoRA方法,数据量化也分两层:
4比特量化(Quantization)
在对 W W W的量化过程中,首先要将参数 W W W归一化使其满足正态分布,即 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1)。通常会采用分块归一化,每一块会有对应的系数 c 1 c_1 c1。
二次量化(Double Quantization)
对于每一个block都会一个系数 c 1 c_1 c1,在计算的过程中我们可以使用高精度数据类型(FT32),但是存储的时候我们也只需要使用低精度数据类型(FT8)就可以了。这样可以进一步减少所需要的内存空间。
基于LoRA算法还有很多改进的方法,感兴趣的同学可以参看[5],列举了一些最新相关成果。
参考文献
[1] LoRA: Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: Low-rank adaptation of large language models. International Conference on Learning Representations (ICLR), 2022
[2] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning. Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing
[3] Hayou, S., Ghosh, N., & Yu, B. (2024). LoRA+: Efficient Low Rank Adaptation of Large Models. arXiv preprint arXiv:2402.12354.
[4] Dettmers, Tim and Pagnoni, Artidoro and Holtzman, Ari and Zettlemoyer, Luke (2023). QLoRA: Efficient Finetuning of Quantized LLMs. arXiv preprint arXiv:2305.14314
[5] https://towardsdatascience.com/an-overview-of-the-lora-family-515d81134725