朴素贝叶斯是一种用于分类和预测任务的算法,他的原理是基于贝叶斯定理。其中朴素的意思是假设各特征之间相互独立。这个实验我是用的老师课后作业的题目预测某天是否会打乒乓球,假设每个特征独立。
目录
贝叶斯公式:
训练集:
处理训练集数据:
先验概率:
后验概率:
思路分析:
代码及其运行结果截图:
总代码及其运行截图:
总代码:
运行结果截图:
实验中遇到的问题:
实验优缺点分析:
优点:
缺点:
贝叶斯公式:
(不知道为什么这个公式不能正常显示)
训练集:

处理训练集数据:
我在程序种用三个变量分别存储,定义一个字典ynum来存储每个预测类别的样本数量在这里也就是存储yes和no的数量,用xnum来存储每个预测类别的样本对应特征的数量。classes是个集合来存储预测的类别。
ynum = defaultdict(int)
xnum = defaultdict(lambda: defaultdict(int))
classes = set()我们先把训练集处理一下得到每个样本种类的数量以及总的数量。看下面代码。通过遍历我们训练集中的数据,每次循环一个数据,假设我们取到第一个数据
| sunny | hot | high | weak | no |
可以看到他有五个变量,我们就对这个进行处理,他的预测类别为no,就把他加入到集合中,再在ynum中对应no标签上加一,表示到这个数据no的数量。接下来就是依次取出sunny, hot, high, weak。我们先取到sunny,在xnum的no标签上的sunny上加上一,表示sunny分类为no的数量,下面依次得到就好了。
leny = len(y)
for i in range(leny):
fea = X[i]
label = y[i]
classes.add(label)
ynum[label] += 1
for fea1 in fea:
xnum[label][fea1] += 1最后我们得到处理完毕的数据。因为是字典型的数据,所以打印除其中的一部分看看。

先验概率:
根据以往经验和分析得到的概率
按照我的理解他就是统计每个类别出现的次数,除以总样本数,计算得到了每个类别的先验概率。
在我这个训练集中只有yes和no两种情况,那么他的先验概率也就是直接样本数除以总数得到。
for label in classes:
ynum[label] /= leny我们打印得到的后验概率得到:
如图所见,他两个分类的先验概率,分类为no的概率为5/14,分类为yes的概率为9/14。

后验概率:
某件事已经发生,想要计算这件事发生的原因是由某个因素引起的概率
思路分析:
后验概率也就是说在某个已知条件下发生,也就是条件概率,这时候就要用到朴素贝叶斯公式
对于每个测试集得到一个对应的预测分类,存储在predictions = [];我们每一次取到一个测试集数据。假设取到的是sunny, mild, normal, strong,我们要预测他是否会外出打乒乓球。我们就要遍历每一种类别得到这个数据预测为改类别的概率。我们用max_prob和predicted_class来记录预测概率最大的类别。因为我们是朴素贝叶斯,是假设每个特征之间相互独立的,所以计算起来就只需要把该类别对应的特征的概率累乘运行就可以得到该类别i下的后验概率,我们在所有类别后验概率中选取概率最大的那一个作为答案即可。
代码及其运行结果截图:
def predict(X):
predictions = []
for fea in X:
maxp = -0.01
ans = None
for label in classes:
p = ynum[label]
for fea1 in fea:
p *= xnum[label][fea1] / sum(xnum[label].values())
if p > maxp:
maxp = p
ans = label
predictions.append(ans)
return predictions运行结果截图:

总代码及其运行截图:
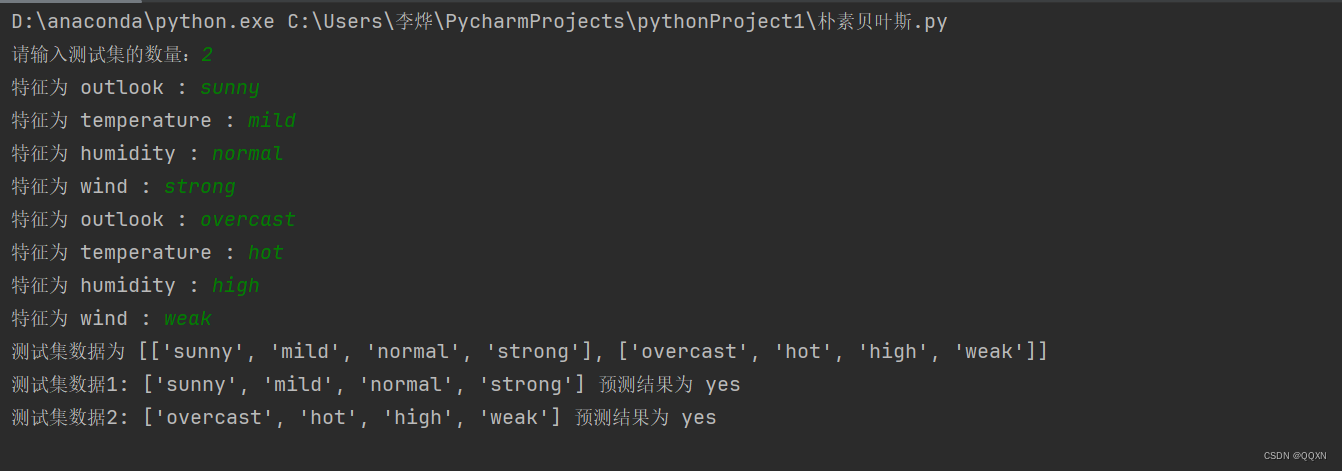
这边的测试集我就选取了两组:
['sunny', 'mild', 'normal', 'strong'], ['overcast', 'hot', 'high', 'weak']
总代码:
from collections import defaultdict
ynum = defaultdict(int)
xnum = defaultdict(lambda: defaultdict(int))
classes = set()
def xygl(X, y):
leny = len(y)
for i in range(leny):
fea = X[i]
label = y[i]
classes.add(label)
ynum[label] += 1
for fea1 in fea:
xnum[label][fea1] += 1
for label in classes:
ynum[label] /= leny
#for label in classes:
# for feature in X[0]:
# print(label,fea, feature_counts[label][fea]);
#for label in classes:
# print(label,"=",class_probabilities[label]);
def predict(X):
predictions = []
for fea in X:
maxp = -0.01
ans = None
for label in classes:
p = ynum[label]
for fea1 in fea:
p *= xnum[label][fea1] / sum(xnum[label].values())
if p > maxp:
maxp = p
ans = label
predictions.append(ans)
return predictions
T = ['outlook','temperature' ,'humidity', 'wind']
X = [
['sunny', 'hot', 'high', 'weak'],
['sunny', 'hot', 'high', 'strong'],
['overcast', 'hot', 'high', 'weak'],
['rain', 'mild', 'high', 'weak'],
['rain', 'cool', 'normal', 'weak'],
['rain', 'cool', 'normal', 'strong'],
['overcast', 'cool', 'normal', 'strong'],
['sunny', 'mild', 'high', 'weak'],
['sunny', 'cool', 'normal', 'weak'],
['rain', 'mild', 'normal', 'weak'],
['rain', 'mild', 'normal', 'strong'],
['overcast', 'mild', 'high', 'strong'],
['overcast', 'hot', 'normal', 'weak'],
['rain', 'mid', 'high', 'strong']
]
y = ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
xygl(X, y)
test_data = []
cnt = int(input("请输入测试集的数量:"))
for t in range(cnt):
sample = []
for i in range(4): # 假设每个样本有4个特征值
test = input(f"特征为 {T[i]} : ")
sample.append(test)
test_data.append(sample)
print("测试集数据为", test_data)
predictions = predict(test_data)
lenp = len(predictions)
for i in range(lenp):
print(f"测试集数据{i+1}:",test_data[i],"预测结果为",predictions[i])
运行结果截图:
实验中遇到的问题:
朴素贝叶斯算法的实现相比于决策树和ROC曲线都相对简单一点,又有给定公式,在算法的实现上相对容易。我在这个所以中遇到的问题主要在对数据集的选择上面,我原本打算直接采用之前的鸢尾花数据集的,但是我在实现算法之后,对测试集进行预测,发现这个程序的预测准确率非常低,几乎是对测试集中的预测都是错误的,朴素贝叶斯法虽然是假设每个特征之间仙湖独立的,但是每个特征之间的相关性对预测结果影响很大,然后就想起了老师上课小测的数据集,比较适合这个实验。
另一个遇到的问题就是数据的处理上面,刚开始没有想到用字典型,就导致我的程序处理数据比较麻烦,局限性比较强,后来学习了一下,改进了我的算法。
实验优缺点分析:
优点:
该算法的实现比较简单,因为假设每个特征相互独立,所以使得这个算法只需要简单的相乘就可以得到结果。相比于knn算法于决策树算法,他的时间和空间复杂度都是较小的,所以对比knn算法和决策树算法,在处理大规模数据上更具有优势,而且在每个特征之间相关性越小,朴素贝叶斯算法的预测结果就会更为准确。
缺点:
朴素贝叶斯算法的缺点也是最明显的,该算法假设了每个特征之间相互独立,而如果特征之间的相关性比较强,那朴素贝叶斯算法的预测准确率就会大大减低。而且在实验中的每一个特征值或多或少都有关联,所以朴素贝叶斯算法的局限性就比较强,容易造成欠拟合。