一、概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者具有以下性质的二叉树：

若它的左子树不为空，则左树上所有节点的值都小于根节点的值。

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。

它的左右子树也分别为二叉搜索树。最多找O(N)。

二、查找、插入、删除

插入

bool Insert(K& k)
{
	
	if (_root == nullptr)
	{
		_root = new BSNode(k);
		return true;
	}
	BSNode* cur = _root;
	BSNode* parent = nullptr;
	while (cur)
	{
		if (cur->_k < k)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_k > k)
		{
			parent = cur;
			cur = cur->_left;
		}
	}
	if (parent->_k < k)
	{
		parent->_right = new BSNode(k);
	}
	else if (parent->_k > k)
	{
		parent->_left = new BSNode(k);
	}
	else
	{
		return false;
	}
	return true;
}

查找

bool Find(K k)
{
	BSNode* cur = _root;
	while (cur)
	{
		if (cur->_k < k)
		{
			cur = cur->_right;
		}
		else if (cur->_k > k)
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	return false;
}

删除

依次删除7、14、3、8。7和14属于直接删除的场景

3、8属于需要替换法进行删除的场景。

1、没有孩子

2、一个孩字

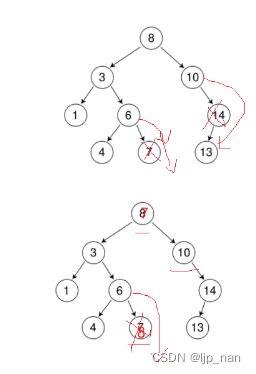
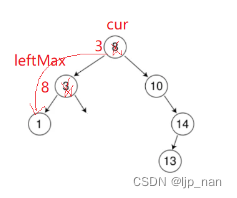
3、两个孩子，需要进行替换，也就是替换法，用左子树的最大节点或者右子树的最小节点。

最大节点为最右节点，最小节点就是最左节点 ，还需要处理要删除的节点为根节点，它没有左子树或者没有右子树的情况。

还有一种情况就是leftmax就是root的左子树的根，此时parent为nullptr所以我们需要让parent = cur

void Erase(K& k)
{
	BSNode* cur = _root;
	BSNode* parent = nullptr;
	while (cur)
	{
		if (cur->_k < k)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_k > k)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			//开始托孤
			//要删除的节点，左孩子为空
			if (cur->_left == nullptr)
			{
				//需要判断删除节点就是根节点的情况
				if (cur == _root)
				{
					_root = cur->_right;
				}
				else
				{
					if (parent->_right == cur)
					{
						parent->_right = cur->_right;
					}
					else
					{
						parent->_left = cur->_right;
					}
				}
				
			}
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_left;
				}
				else
				{
					if (parent->_right == cur)
					{
						parent->_right = cur->_left;
					}
					else 
					{
						parent->_left = cur->_left;
					}
				}
			}
			else //两个孩子的情况，就需要替代法来删除
			{
				//找到左子树中最大的节点
				BSNode* leftMax = cur->_left;
				//注意为什么这里等于cur;
				BSNode* parent = cur;  
				while (leftMax->_right)
				{
					parent = leftMax;
					leftMax = leftMax->_right;
				}
				//找到以后把删除节点和leftmax节点的值做交换
				std::swap(cur->_k, leftMax->_k);

				//我们该把父亲的那个孩子和cur节点的孩子连接起来呢需要判断
				if (parent->_left == leftMax)
				{
					parent->_left = leftMax->_left;
				}
				else
				{
					parent->_right = leftMax->_left;
				}

				cur = leftMax;
			}

			delete cur;
			cur = nullptr;
		}
	}
}

有序数组：二分查找，问题：插入删除效率不行

二叉搜索树：插入删除效率还行。

如果退化成下面的情况，插入删除的效率就变成了O(N)，所以我们引出了AVL树红黑树B树系列。

接下来我们看一下递归版本的删除，插入和发现

bool _EraseR(BSNode*& root, const K& k)
{
	
	if (root == nullptr)
	{
		return false;
	}
	if (root->_k < k)
	{
		_EraseR(root->_right, k);
	}
	else if (root->_k > k)
	{
		_EraseR(root->_left, k);
	}
	else
	{
		BSNode* del = root;
		if (root->_left == nullptr)
		{
			root = root->_right;
		}
		else if (root->_right == nullptr)
		{
			root = root->_left;
		}
		else
		{
			BSNode* leftMax = root->_left;
			while (leftMax->_right)
			{
				leftMax = leftMax->_right;
			}
			std::swap(leftMax->_k, root->_k);

			return _EraseR(root->_left, k);
		}
		delete del;
		del = nullptr;
		return true;
	}
}
bool _InsertR(BSNode*& root,const K& k)
{
	if (root == nullptr)
	{
		root = new BSNode(k);
		return true;
	}
	if (root->_k < k)
	{
		_InsertR(root->_right, k);
	}
	else if (root->_k > k)
	{
		_InsertR(root->_left, k);
	}
	else
	{
		return false;
	}
}
bool _FindR(BSNode* root, const K& k)
{
	if (root == nullptr)
		return false;
	BSNode* cur = root;
	if (cur->_k < k)
	{
		_FindR(root->_right, k);
	}
	else if (cur->_k > k)
	{
		_FindR(root->_left, k);
	}
	else
	{
		return true;
	}
}