地表温度LST(Land Surface Temperature)是区域和全球尺度上陆地表层系统过程的关键参数,它综合了地表与大气的相互作用以及大气和陆地之间能量交换的结果。地表温度作为众多基础学科和应用领域的一个关键参数,能
够提供地表能量平衡状态的时空变化信息,在农业干旱、农作物估产、火灾监测、数值预报、全球环流模式以及区域气候模式等研究领域得到广泛的应用。精确的地表温度不仅有助于评估地表能量与水文平衡、热惯量和土壤湿度,而且有助于获取全球表面温度及掌握其长期的变化。
长久以来,人们普遍采用地面站点观测的方式获得地表温度。然而,受太阳辐射、地形地貌、地表覆盖、大气环流等因素的影响,地表温度的动态变化性强,因此地面站点观测获取的地表温度区域代表性有限,无法精确表征区域或全球尺度地表温度的时空分布特征,严重制约了地球科学领域某些学科的深入研究与发展。要获取区域和全球尺度上地表温度的时空分布,常规的地面定点观测难以实现,而卫星遥感技术是唯一可能的手段。
随着科学技术的进步,新兴的热红外遥感( Thermal Infrared remote sensing )技术为高时效、高精度获取区域或全球尺度的地表温度带来了曙光。热红外遥感是一种通过热红外谱段对检测物体发射的热辐射进行探测的技术,它利用物体吸收和发射辐射的物理特性,通过测量目标物体发射的红外辐射的强度、分布和光谱等参数,来了解目标物体的热学特性、表面温度分布等信息。热红外遥感对研究全球能量变换和可持续发展具有重要的意义,在地表温度反演、城市热岛效应、林火监测、旱灾监测、探矿、探地热,岩溶区探水等领域都有很广泛的研究。
⛄辐射物理量基本概念
[1]阎广建,谢天,穆西晗.辐射物理量概念介绍[J].遥感学报,2023,27(10):2445-2448.
定量遥感研究的前提是量化遥感传感器接收的电磁波信息。遥感传感器通过获取从目标物反射和辐射的电磁波能量来得到所需的信息,所以遥感探测通常意义上指的是对电磁波辐射能量的测定。物理学把某个物理量在空间中的分布称为场,如温度场、引力场、电场、磁场等。电磁波辐射能量在空间中的分布被称为辐射场。几乎所有物体都可以作为产生辐射场的辐射源,因为任何温度大于绝对零度的物体,都以电磁波的形式向周围辐射能量,并且几乎所有物体都可以反射外界辐射。辐射源可以被简单地划分为点源和面源。
-
点源是一种理想的情况,辐射源的大小可以忽略不计,近似为一个点,点源可以向四面八方发射能量;当辐射源的大小不可忽略不计,不能被近似为一个点时,需要当作面源。
-
整个面源的辐射可以基于微面元的积分得到,每个微面元往往被近似为平面。一个无限大平面可将三维空间分割为两部分,每个部分都是一个半球空间,辐射可以从微面元出射到半球空间,也可以从半球空间入射被微面元所接收。
遥感传感器直接接收的是电磁波的辐射能量,然而这些辐射能量产生的时间长短、空间范围、方向和角度范围并不确定。因此,需要引出一系列辐射物理量,对物体发射或反射电磁波能量的能力统一描述:
-
辐射能量 Q Q Q(
Radiant Energy):电磁波所传输的能量称为辐射能量,国际单位制 (以下简称SI)单位为焦耳 ( J J J)。辐射能量是最基础的辐射物理量,不会随着时间、空间、角度等物理量的积分而改变量纲,也因此在不加限定的情况下单独一个辐射能量数值不能表征电磁波辐射的强弱,于是基于辐射能量进一步定义以下物理量。 -
辐射通量 Φ \Phi Φ(
Radiant Flux):单位时间内通过任一平面或曲面的辐射能量,也称为辐射功率,国际单位制的基本单位为瓦特 ( W W W),即焦耳/秒( J / s J/s J/s)。辐射通量定义式为:
Φ = d Q d t \Phi=\frac{ {\rm d}Q}{ {\rm d}t} Φ=dtdQ -
辐射通量密度 (
Radiant Flux Density):单位时间内通过单位平面面积的辐射能量,国际单位制的基本单位为瓦特每平方米 ( W / m 2 W/m^2 W/m2)。根据辐射的方向又可以分成辐照度和辐射出射度,分别表示单位面积接收或向外辐射的辐射通量。辐照度和辐射出射度描述的电磁波传输方向相反。此外,不论是平面还是曲面,它们都被划分为无限个微面元,辐照度和辐射出射度均是针对微面元而定义的。要得到整个表面的辐射通量,可以对辐射通量密度在整个表面求积分得到。辐照度和辐射出射度都可以表示为:
E , M = d Φ d A E,M=\frac{ {\rm d}\Phi}{ {\rm d}A} E,M=dAdΦ- 辐照度
E
E
E(
Irradiance):物体表面接收的辐射通量密度。 - 辐射出射度
M
M
M (
Radiant Exitance):面辐射源表面发出的辐射通量密度。
- 辐照度
E
E
E(
-
辐射强度 I I I(
Radiant Intensity):点源在某一给定方向上单位立体角内发出的辐射通量。国际单位制的基本单位为瓦特每球面度 ( W / s r W/sr W/sr)。辐射强度定义式为: I = d Φ / d Ω I={\rm d}\Phi/{\rm d}\Omega I=dΦ/dΩ。式中立体角常用希腊字母 Ω \Omega Ω表示。
I = d Φ d Ω I=\frac{ {\rm d}\Phi}{ {\rm d}\Omega} I=dΩdΦ(1)某立体角的大小可以被简单地定义为该立体角投影到一个以其顶点为球心的球面时,投影的球面面积A与球半径r平方的比值: Ω = A / r 2 \Omega=A/r^2 Ω=A/r2
(2)立体角的单位用球面度 ( s r sr sr) 表示,假设一个球半径为 r r r,其表面积为 4 π r 2 4\pi{r^2} 4πr2,所以整个球面对球心张成的立体角是 4 π 4{\pi} 4π,而半球空间的立体角为 2 π 2{\pi} 2π。
(3)对于一个以 θ \theta θ为天顶角、 φ \varphi φ为方位角的立体角微元 d Ω {\rm d}\Omega dΩ,它在以其顶点为球心的球面上截得的面积可以近似用矩形的面积求得: d Ω = d A / r 2 = r d θ ⋅ r sin θ d φ / r 2 = sin θ d θ d φ {\rm d}\Omega={\rm d}A/r^2=r{\rm d}\theta·r\sin{\theta}{\rm d}\varphi/r^2=\sin{\theta}{\rm d}{\theta}{\rm d}{\varphi} dΩ=dA/r2=rdθ⋅rsinθdφ/r2=sinθdθdφ
(4)对于面辐射源,定义辐射亮度来描述其在不同方向的辐射能力。
-
辐射亮度 L L L (
Radiance):简称辐亮度,描述的是面辐射源在某一方向单位立体角单位时间内,垂直于辐射方向单位面积上的辐射能量。国际单位制的基本单位是瓦特每球面度每平方米 ( W ⋅ s r − 1 ⋅ m − 2 W·sr^{-1}·m^{-2} W⋅sr−1⋅m−2)。辐亮度定义式为:
L = d 2 Φ d Ω d A cos θ = d I d A cos θ = d M d Ω cos θ L=\frac{ {\rm d^2}\Phi}{ {\rm d}\Omega{\rm d}A\cos{\theta} }=\frac{ {\rm d}I}{ {\rm d}A\cos{\theta} }=\frac{ {\rm d}M} { {\rm d}\Omega\cos{\theta} } L=dΩdAcosθd2Φ=dAcosθdI=dΩcosθdM
式中, θ \theta θ是辐射方向与辐射面源法线夹角。对于无限大的各向同性面辐射源,辐亮度不随观测角度的变化而变化。
遥感传感器一般不在全部光谱范围内收集能量,而是在特定的波段内接收能量。为描述特定波段内的辐射物理量,在上述辐射物理量的名称前均可加上“光谱”两字,表示单位波长宽度的辐射物理量,对应的表达式需在原有定义式基础上再对波长求导。例如,光谱辐射亮度 (Spectral Radiance)表示的是单位波长宽度的辐射亮度,单位是瓦特每球面度每平方米每微米 (
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
−
1
W·sr^{-1}·m^{-2}·μm^{-1}
W⋅sr−1⋅m−2⋅μm−1)。
一般来说,面辐射源向不同方向的辐射能力是不同的,也就是说,观察者在不同方向上测量的辐亮度值不同。特别地,各角度观察到的辐亮度相同的辐射源称为朗伯体 (朗伯源),辐亮度大小和角度有关的辐射源称为非朗伯体。对于朗伯体,根据辐亮度定义,可以计算它在 2 π 2{\pi} 2π空间内的辐射出射度: M = π L M=\pi{L} M=πL,可见,朗伯体在 2 π 2{\pi} 2π空间内的辐射出射度在数值上是辐亮度的 π {\pi} π倍。
辐射能量和辐射通量是相对基础的辐射物理量,在它们的基础上派生的辐照度和辐射出射度,是地表辐射能量平衡计算等应用中常用的关键参量。当被观测表面的尺寸小于像元大小时,适合用辐射强度表征所接收的辐射信号,比如在天文领域。而遥感往往观测的是远大于像元大小的物体表面,适用辐亮度的概念。辐亮度限定了单位时间、单位投影面积、单位立体角的辐射,便于不同传感器接收电磁辐射信号的比较,是辐射传输理论中的常用物理量。实际应用中,传感器先将接收到的电磁波转换为电信号数值,经过辐射定标后可以直接转为辐亮度。
光谱响应曲线:光谱响应函数是表示传感器性能的一个关键参数,描述了传感器对不同波长的光的响应程度,它反应了传感器的线性度、灵敏度和选择性等特征,在创建和评估传感器的功效时,必须考虑到光谱响应函数。光谱响应函数文件通常由两列组成,一列代表波长或波数,另一列代表波长对应的响应函数值。
热力学温度:热力学温度是热力学当中的基本参数之一,又被称为动力学温度,它是温度的一个特殊定义,由热力学第二定律得到,单位是开尔文( K K K)。热力学温度描述了物体的热状态,表现形式为物质内部分子间能量的传递。热力学温度是世界七大基本物理量之一,热力学温度的最低温度是绝对零度(0 K K K),即:零点。
亮度温度:亮度温度是指黑体辐射的温度,物体的亮度温度等于辐射温度相同的黑体的物理温度。简单来说,亮度温度是一个普通的温度概念,具有温度的量纲,但不具有温度的物理意义。在一定条件下,亮度温度与物体的实际温度有一定的关系,但并不总是一致的,通常情况下,亮度温度与实际温度的偏差来自于表面辐射率和大气的影响。
⛄黑体辐射的基本规律
👀基尔霍夫定律(1859年)
基尔霍夫定律表明:任何物体在任意给定的温度(
T
T
T)和波长(
λ
\lambda
λ)条件下,其辐射通量密度
M
(
T
,
λ
)
M(T,\lambda)
M(T,λ)和吸收系数
α
(
T
,
λ
)
\alpha(T,\lambda)
α(T,λ)之比是一个常数,等于同一温度波长下,绝对黑体的辐射通量密度
M
b
(
T
,
λ
)
M_b(T,\lambda)
Mb(T,λ):
M
b
(
T
,
λ
)
=
M
(
T
,
λ
)
α
(
T
,
λ
)
M_b(T,\lambda)=\frac{M(T,\lambda)}{\alpha(T,\lambda)}
Mb(T,λ)=α(T,λ)M(T,λ)
因此,物体的吸收率越大,辐射能力就越强,即黑体的辐射能量最大。 发射率是物体辐射能力的度量,其定义为:在同一给定温度(
T
T
T)和波长(
λ
\lambda
λ)下,物体的辐射能力与黑体辐射能力之比。由定义可知,发射率为值在0~1之间无量纲的量,物体的发射率与物体的组成成分、表面状态、物理性质等因素有关。根据定义,发射率的表达式如下:
ε
(
T
,
λ
)
=
M
(
T
,
λ
)
M
b
(
T
,
λ
)
\varepsilon(T,\lambda)=\frac{M(T,\lambda)}{M_b(T,\lambda)}
ε(T,λ)=Mb(T,λ)M(T,λ)
故有:
ε
(
T
,
λ
)
=
α
(
T
,
λ
)
\varepsilon(T,\lambda)=\alpha(T,\lambda)
ε(T,λ)=α(T,λ),即物体的吸收率等于它的发射率。
👀斯特藩-玻尔兹曼定律(1879年和1884年)
斯特藩定律是现代热力学领域的基本定律,描述了物体的温度与辐射之间的关系。具体来说,当物体的温度不为零时,它会发出电磁辐射,其能量密度与温度有关。1879年物理学家约瑟夫斯特藩经过多年整理各种实验的结果得出了这个定律。1884 年,物理学家、路德维希·玻尔兹曼根据热力学理论,实验性地假设用光能(电磁辐射)代替气体作为电热机的工作介质,最终成功地推导出与斯特藩归纳相同的结论。 斯特藩定律的内容为:一个黑体在单位时间内的黑体辐射出射度
j
∗
j^*
j∗与其本身具有的热力学温度
T
T
T的四次方呈正比关系,即:
j
∗
=
ε
σ
T
4
j^*=\varepsilon\sigma{T^4}
j∗=εσT4
式中,物体的辐射出射度
j
∗
j^*
j∗的单位为
W
/
m
2
W/m^2
W/m2,国际单位制标准单位为:
J
/
(
s
⋅
m
2
)
J/(s·m^2)
J/(s⋅m2);
T
T
T为黑体的热力学温度,单位是开尔文(
K
K
K);
ε
\varepsilon
ε为物体的发射率,黑体的发射率为1;系数
σ
\sigma
σ为斯特藩常量,单位为:
W
/
(
m
2
⋅
K
4
)
W/(m^2·K^4)
W/(m2⋅K4)。若一个黑体的温度增加一倍,则它的辐射出射度会增加16倍。
σ
=
2
π
5
k
4
15
c
2
h
3
=
5.67032
×
1
0
−
8
\sigma=\frac{2\pi^5k^4}{15c^2h^3}=5.67032×10^{-8}
σ=15c2h32π5k4=5.67032×10−8
其中,
h
h
h为普朗克常数,
h
=
6.6262
×
1
0
−
34
J
⋅
s
h=6.6262×10^{-34}J·s
h=6.6262×10−34J⋅s;
c
c
c为光速,
c
=
2.998
×
1
0
8
m
/
s
c=2.998×10^8m/s
c=2.998×108m/s;
k
k
k为玻尔兹曼常数,
k
=
1.3806
×
1
0
−
23
J
/
K
k=1.3806×10^{-23}J/K
k=1.3806×10−23J/K。该定律表明:物体的热力学温度越高其辐射的电磁波能量越强;受发射率的影响,当一个物体为黑体时辐射能力最强;具有相同温度的地物,会因为发射率的不同导致完全不同的辐射出射度。
👀维恩位移定律(1893年)
维恩位移定律是物理学中的一个基本定律,它解释了黑体辐射中峰值波长与温度之间相关性。1893年,德国物理学家威廉·维恩,通过多年对大量实验数据研究的丰富经验总结,提出了维恩位移定律,该定律研究表明,当一个物体被加热时,其辐射的波长分布会发生变化,峰值波长会随温度的升高而变短,即呈现负相关,它的数学表示为:
λ
m
a
x
=
b
T
\lambda_{max}=\frac{b}{T}
λmax=Tb
式中,
λ
m
a
x
\lambda_{max}
λmax为对应于黑体辐射亮度最大值的波长,单位为
μ
m
μm
μm;
b
b
b为比例常数,成为维恩位移常数,
b
=
2897.8
μ
m
⋅
K
b=2897.8μm·K
b=2897.8μm⋅K;
T
T
T为黑体的绝对温度,单位为开尔文(
K
K
K)。维恩定律表明,一个物体的温度越高,其辐射的峰值波长越短。
👀普朗克辐射定律(1900年)
普朗克定律(Planck’s law),也被称为黑体辐射定律,是描述黑体辐射的物理定律之一,解释了黑体辐射能量根据一定波长的分布。根据普朗克定律,绝对温度大于0
K
K
K的任何物体都会向外以电磁波的形式辐射能量。1900年,普朗克引进量子理论并将黑体辐射源视为离散的量子发射,推导出绝对黑体辐射源辐射出射度(
M
M
M)随着波长(
λ
\lambda
λ)和温度(
T
T
T)的分布函数,并且能够与实验精确的吻合,该分布函数如下:
M
(
T
,
λ
)
=
2
π
h
c
2
λ
5
[
e
x
p
(
c
h
k
λ
T
)
−
1
]
=
C
1
λ
5
[
e
x
p
(
C
2
λ
T
)
−
1
]
M(T,\lambda)=\frac{2{\pi}hc^2}{\lambda^5[exp(\frac{ch} {k\lambda{T} })-1]}=\frac{C_1}{\lambda^5[exp(\frac{C_2}{\lambda{T} })-1]}
M(T,λ)=λ5[exp(kλTch)−1]2πhc2=λ5[exp(λTC2)−1]C1
式中,
M
M
M为黑体辐射出射度,单位为
W
⋅
m
−
2
⋅
μ
m
−
1
W·m^{-2}·μm^{-1}
W⋅m−2⋅μm−1;
h
h
h为普朗克常数,
h
=
6.6262
×
1
0
−
34
J
⋅
s
h=6.6262×10^{-34}J·s
h=6.6262×10−34J⋅s;
c
c
c为光速,
c
=
2.998
×
1
0
8
m
/
s
c=2.998×10^8m/s
c=2.998×108m/s;
k
k
k为玻尔兹曼常数,
k
=
1.3806
×
1
0
−
23
J
/
K
k=1.3806×10^{-23}J/K
k=1.3806×10−23J/K;
λ
\lambda
λ为波长,单位为
μ
m
μm
μm;
T
T
T为热力学温度,单位为
K
K
K;
C
1
C_1
C1和
C
2
C_2
C2分别为第一、第二辐射常数,大小分别为:
C
1
=
2
π
h
c
2
=
3.74203
×
1
0
8
W
⋅
m
−
2
⋅
μ
m
4
C_1=2\pi{h}c^2=3.74203×10^8W·m^{-2}·μm^{4}
C1=2πhc2=3.74203×108W⋅m−2⋅μm4,
C
2
=
c
h
/
k
=
14388
μ
m
⋅
K
C_2=ch/k=14388μm·K
C2=ch/k=14388μm⋅K。
注意单位换算的问题:(这里暂时只考虑单位,不考虑数值)
C 1 = 2 π h c 2 = J ⋅ s ⋅ m 2 ⋅ s − 2 = W ⋅ m 2 C_1=2\pi{h}c^2=J·s·m^2·s^{-2}=W·m^2 C1=2πhc2=J⋅s⋅m2⋅s−2=W⋅m2,注意 M M M的单位用的是 W ⋅ m − 2 ⋅ μ m − 1 W·m^{-2}·μm^{-1} W⋅m−2⋅μm−1,那么 C 1 / λ 5 C_1/\lambda^5 C1/λ5的单位也必须是 W ⋅ m − 2 ⋅ μ m − 1 W·m^{-2}·μm^{-1} W⋅m−2⋅μm−1,所以:
C 1 / λ 5 = W ⋅ m 2 μ m 5 = W ⋅ m − 2 ⋅ m 4 μ m 5 = 1 0 24 ⋅ W ⋅ m − 2 ⋅ μ m 4 μ m 5 C_1/\lambda^5=\frac{W·m^2} {μm^5}=\frac{W·m^{-2}·m^4} {μm^5}=\frac{10^{24}·W·m^{-2}·μm^4}{μm^5} C1/λ5=μm5W⋅m2=μm5W⋅m−2⋅m4=μm51024⋅W⋅m−2⋅μm4,即 C 1 C_1 C1的计算结果必须乘以 1 0 24 10^{24} 1024。
C 2 = c h k = m ⋅ s − 1 ⋅ J ⋅ s J ⋅ K − 1 = m ⋅ K = 1 0 6 ⋅ μ m ⋅ K C_2=\frac{ch}{k}=\frac{m·s^{-1}·J·s}{J·K^{-1} }=m·K=10^6·μm·K C2=kch=J⋅K−1m⋅s−1⋅J⋅s=m⋅K=106⋅μm⋅K,即 C 2 C_2 C2的计算结果必须乘以 1 0 6 10^6 106。
⛄红外辐射传输基础理论
[1]李召良,段四波,唐伯惠,等.热红外地表温度遥感反演方法研究进展[J].遥感学报,2016,20(05):899-920
根据普朗克定律(Planck’s law),绝对温度大于0
K
K
K的任何物体都会向外以电磁波的形式辐射能量。处于热平衡状态下的黑体在温度
T
T
T和波长
λ
\lambda
λ处的辐射能量可以用普朗克定律表示,即:
B
λ
(
T
)
=
C
1
λ
5
[
e
x
p
(
C
2
λ
T
)
−
1
]
B_\lambda(T)=\frac{C_1}{\lambda^5[exp(\frac{C_2}{\lambda{T} })-1]}
Bλ(T)=λ5[exp(λTC2)−1]C1
式中,
B
λ
(
T
)
B_\lambda(T)
Bλ(T)是黑体在温度
T
(
K
)
T(K)
T(K)和波长
λ
(
μ
m
)
\lambda(μm)
λ(μm)处的光谱辐亮度(
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
−
1
W·sr^{-1}·m^{-2}·μm^{-1}
W⋅sr−1⋅m−2⋅μm−1);
C
1
C_1
C1和
C
2
C_2
C2分别是物理常量:
C
1
=
2
h
c
2
=
1.19113
×
1
0
8
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
4
C_1=2{h}c^2=1.19113×10^8W·sr^{-1}·m^{-2}·μm^{4}
C1=2hc2=1.19113×108W⋅sr−1⋅m−2⋅μm4,
C
2
=
c
h
/
k
=
1.439
×
1
0
4
μ
m
⋅
K
C_2=ch/k=1.439×10^4μm·K
C2=ch/k=1.439×104μm⋅K。(小编反复计算后,上下两种方式的
C
1
C_1
C1是
π
{\pi}
π倍关系)
由于绝大多数自然地物都是非黑体,它们的热辐射需要在上式中加入地表发射率 ε \varepsilon ε的影响。地表发射率可定义为地物的实际热辐射与同温同波长下黑体热辐射的比值。自然地物的热辐射可以用地表发射率乘以上式的普朗克函数得到。显然,如果大气对卫星获取的辐亮度信号没有影响,那么在已知地表发射辐射和发射率的情况下,地表温度就能根据上式反演得到。
黑体在特定温度 T ( K ) T(K) T(K)下单色辐射强度的极大值所对应的波长 λ m a x \lambda_{max} λmax可以用维恩位移定律表示,根据这一性质,对于温度在(250—330) K K K的地表来说,其峰值波长 λ m a x \lambda_{max} λmax主要处于热红外波长范围(8.8—11.6) μ m μm μm,而对于诸如火灾、火山喷发的高温地表,其温度可高于800 K K K,那么它们的峰值波长 λ m a x \lambda_{max} λmax主要处于中红外波长范围(3—5) μ m μm μm。因此,可以根据不同的需求选择不同的波长范围来探测地表热辐射状况。
卫星红外传感器能够接收到视线方向上来自地表经大气传输的辐射信息。在局地热平衡的晴空无云条件下,根据辐射传输方程,传感器在大气顶部所接收到的通道辐亮度
I
i
I_i
Ii可以表示为
I
i
(
θ
,
φ
)
=
R
i
(
θ
,
φ
)
τ
i
(
θ
,
φ
)
+
R
a
t
i
↑
(
θ
,
φ
)
+
R
s
l
i
↑
(
θ
,
φ
)
I_i(\theta,\varphi)=R_i(\theta,\varphi)\tau_i(\theta,\varphi)+R_{a t_i \uparrow}(\theta,\varphi)+R_{s l_i \uparrow}(\theta,\varphi)
Ii(θ,φ)=Ri(θ,φ)τi(θ,φ)+Rati↑(θ,φ)+Rsli↑(θ,φ)
式中,地表辐亮度
R
i
R_i
Ri可以表示为
R
i
(
θ
,
φ
)
=
ε
i
(
θ
,
φ
)
B
i
(
T
s
)
+
[
1
−
ε
i
(
θ
,
φ
)
]
R
a
t
i
↓
+
[
1
−
ε
i
(
θ
,
φ
)
]
R
s
l
i
↓
+
ρ
b
i
(
θ
,
φ
,
θ
s
,
φ
s
)
×
E
i
cos
(
θ
s
)
τ
i
(
θ
s
,
φ
s
)
\begin{aligned} & R_i(\theta,\varphi)=\varepsilon_i(\theta,\varphi) B_i\left(T_s\right)+\left[1-\varepsilon_i(\theta, \varphi)\right] R_{a t_i \downarrow}+{\left[1-\varepsilon_i(\theta, \varphi)\right] R_{s l_i \downarrow}+\rho_{b i}\left(\theta, \varphi,\theta_s,\varphi_s\right) \times} E_i \cos \left(\theta_s\right) \tau_i\left(\theta_s, \varphi_s\right)\end{aligned}
Ri(θ,φ)=εi(θ,φ)Bi(Ts)+[1−εi(θ,φ)]Rati↓+[1−εi(θ,φ)]Rsli↓+ρbi(θ,φ,θs,φs)×Eicos(θs)τi(θs,φs)
式中,
θ
\theta
θ和
φ
\varphi
φ分别表示观测天顶角和观测方位角,为简单起见,观测天顶角和方位角在之后公式中将被忽略。
τ
i
\tau_i
τi是通道
i
i
i的大气等效透过率;
ε
i
\varepsilon_i
εi和
T
s
T_s
Ts分别是通道
i
i
i地表发射率和地表温度;
R
a
t
i
↓
R_{a t_i \downarrow}
Rati↓是大气下行热辐射,
R
s
l
i
↓
R_{s l_i \downarrow}
Rsli↓是大气散射的下行太阳辐射;
ρ
b
i
\rho_{b i}
ρbi是地表双向反射率,
E
i
E_i
Ei是大气顶部的太阳辐照度,
θ
s
\theta_s
θs和
φ
s
\varphi_s
φs分别是太阳天顶角和方位角。
-
路径①: R i τ i R_i \tau_i Riτi表示经大气衰减之后的近地表处辐亮度(经大气衰减之后的地表离地辐射);
-
路径②: R a t i ↑ R_{a t_i \uparrow} Rati↑表示大气上行热辐射;
-
路径③: R s l i ↑ R_{s l_i \uparrow} Rsli↑表示大气散射的上行太阳辐射;
-
路径④: ε i B i ( T S ) \varepsilon_i B_i\left(T_S\right) εiBi(TS);表示地表自身发射的辐亮度;
-
路径⑤和⑥: ( 1 − ε i ) R a t i ↓ \left(1-\varepsilon_i\right) R_{a t_i \downarrow} (1−εi)Rati↓和 ( 1 − ε i ) R s l i ↓ \left(1-\varepsilon_i\right) R_{s l_i \downarrow} (1−εi)Rsli↓分别表示经地表反射的下行大气热辐射和散射的太阳辐射;
-
路径⑦: ρ b i E i cos ( θ s ) τ i ( θ s , φ s ) \rho_{b i} E_i \cos \left(\theta_s\right) \tau_i\left(\theta_s, \varphi_s\right) ρbiEicos(θs)τi(θs,φs)表示经地表反射的太阳直射辐射。
由于在8—14
μ
m
μm
μm波谱区的白天和夜间数据和3—5
μ
m
μm
μm波谱区的夜间数据中,大气顶部的太阳辐射可以忽略不
计,因此上式中太阳辐射部分(路径③⑥和⑦)均可以忽略,而不会影响精度。
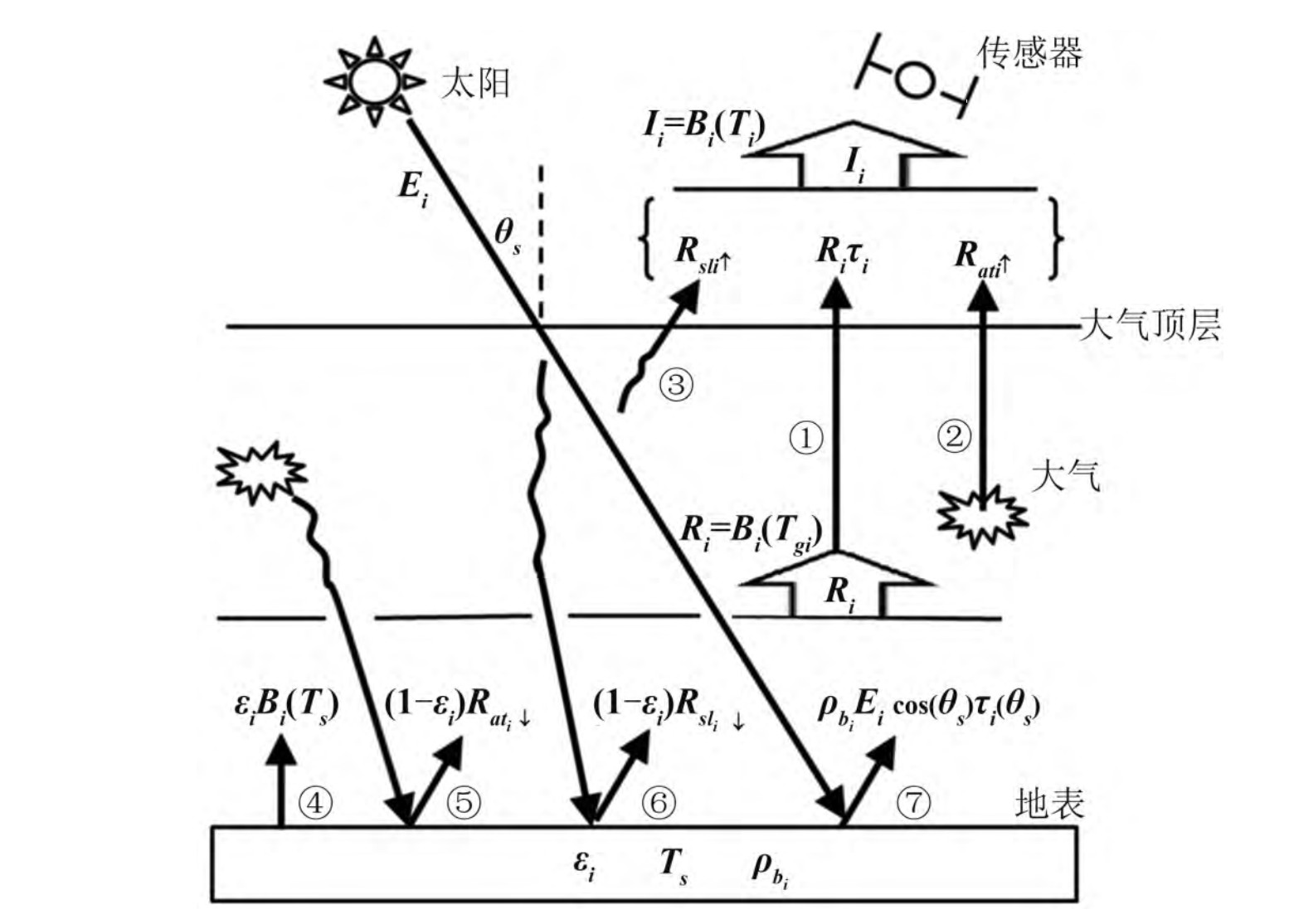
为了方便和数学简写起见,大气顶部辐亮度 I i I_i Ii和地表辐亮度 R i R_i Ri一般用亮度温度来表示,即发射率为1。大气顶部亮温 T i T_i Ti和地表亮温 T g i T_{gi} Tgi定义为: B i ( T i ) = I i B_i\left(T_i\right)=I_i Bi(Ti)=Ii, B i ( T g i ) = R i B_i\left(T_{g i}\right)=R_i Bi(Tgi)=Ri
值得注意的是,上式中除了角度变量
(
θ
,
φ
,
θ
s
,
φ
s
)
(\theta, \varphi,\theta_s,\varphi_s)
(θ,φ,θs,φs),其他的变量和参数都是通道等效值。大多数的卫星传感器都只能探测有限光谱带宽的辐射信号。各参数的通道等效值通过加权平均计算,表达式为:
X
i
=
∫
λ
1
λ
2
g
i
(
λ
)
X
λ
d
λ
∫
λ
1
λ
2
g
i
(
λ
)
d
λ
X_i=\frac{\int_{\lambda_1}^{\lambda_2}\,g_i(\lambda)X_\lambda{\rm d}{\lambda}}{\int_{\lambda_1}^{\lambda_2}\,g_i(\lambda){\rm d}{\lambda}}
Xi=∫λ1λ2gi(λ)dλ∫λ1λ2gi(λ)Xλdλ
式中,
g
i
(
λ
)
g_i(\lambda)
gi(λ)是通道
i
i
i的光谱响应函数,
λ
1
\lambda_1
λ1和
λ
2
\lambda_2
λ2分别是通道
i
i
i的波长下边界和上边界,
X
X
X代表
B
(
T
)
B(T)
B(T),
I
I
I,
R
R
R,
R
a
t
i
↑
R_{a t_i \uparrow}
Rati↑,
R
s
l
i
↑
R_{s l_i \uparrow}
Rsli↑,
R
a
t
i
↓
R_{a t_i \downarrow}
Rati↓,
R
s
l
i
↓
R_{s l_i \downarrow}
Rsli↓,
E
E
E,
ε
\varepsilon
ε,
τ
\tau
τ和
ρ
b
\rho_b
ρb。
⛄热红外辐射传输方程
地表热辐射传输方程是描述热辐射传播通过介质时与介质发生相互作用( 吸收、散射、发射等)而使热辐射能按一定规律传输的方程。遥感器所接受到的热辐射主要有由地表热辐射经大气衰减后被遥感器接受的热辐射( 即被测目标本身的热辐射) 、大气向上的热辐射( 大气直接热辐射) 和大气向下热辐射( 大气向地面的热辐射) 经地表反射后又被大气衰减最终被遥感器接受的热辐射3部分。
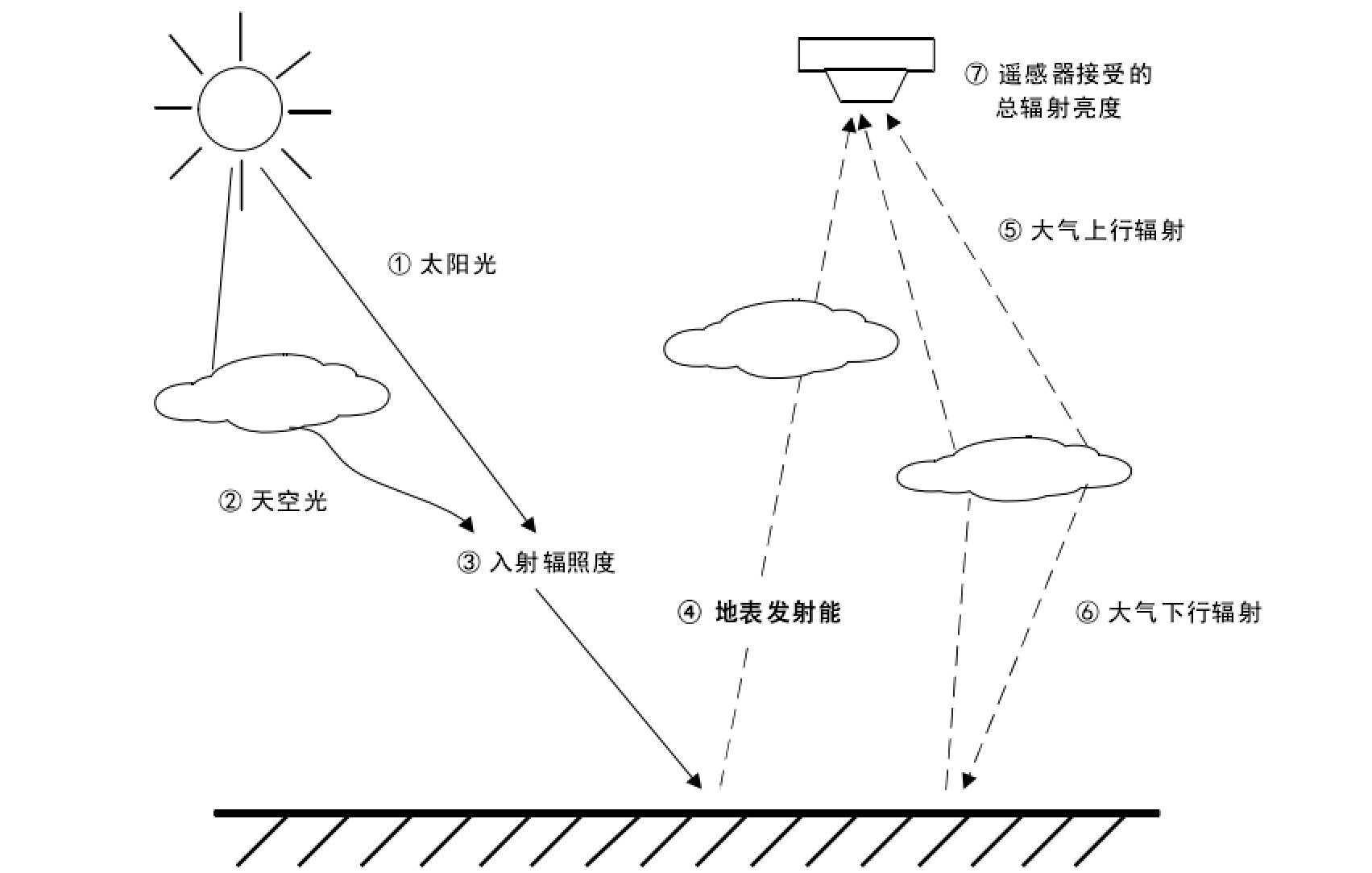
上图展示了热红外辐射的传输过程,地物和大气最主要的辐射来源是太阳,太阳光穿透大气到达地面后,地表吸收太阳辐射能开始升温,然后,将吸收的太阳能转换为自身热能后再向外发射能量,最后,地面发射的能量经过大气的散射、吸收和发射后到达传感器。大气不仅是削弱热红外辐射的介质,大气本身也会向外发射辐射,因此传感
器不仅会接收到大气自身的上行辐射,还会接收到经过大气衰减的地面反射的大气下行辐射。
大气热红外辐射的性质很复杂,大气中最主要的吸收物质是水汽,水汽在6.3
μ
m
μm
μm有一个较强的吸收带,占有较宽的谱段;大气在14
μ
m
μm
μm以上可近似看作黑体,14
μ
m
μm
μm以上的热红外辐射无法穿透大气。因此在地-气辐射传输过程中,地表热辐射可以通过3-5
μ
m
μm
μm和8-14
μ
m
μm
μm两个大气窗口,MODTRAN的中纬度夏季模型对应的大气透过率如下图:
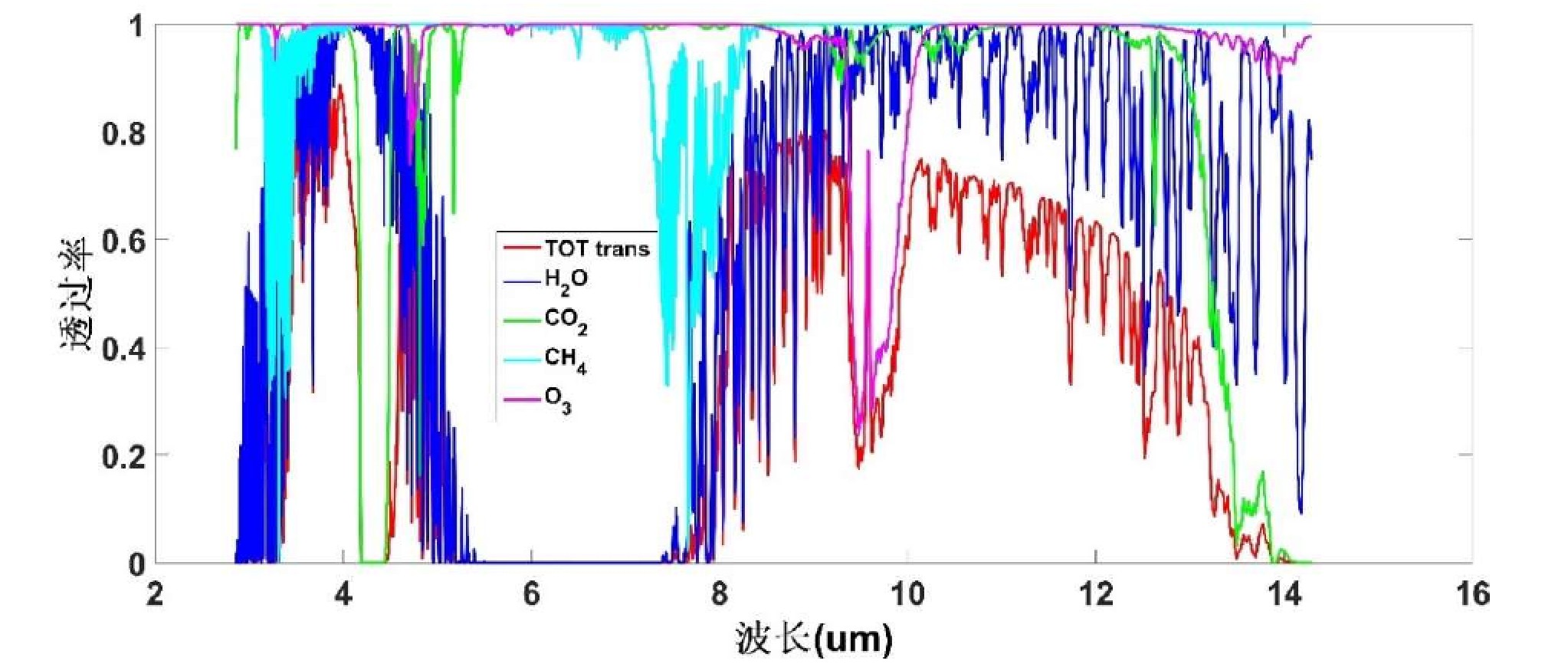
在局地热平衡及地表对大气热辐射具有朗伯体性质的假设下,根据辐射传输理论,在晴空大气下,热红外大气辐射传输方程可以表示为:
L
s
e
n
=
B
λ
(
T
i
)
=
τ
λ
(
θ
)
⋅
[
ε
λ
⋅
B
λ
(
T
s
)
+
(
1
−
ε
λ
)
⋅
L
λ
↓
]
+
L
λ
↑
L_{sen}=B_\lambda(T_i)=\tau_\lambda(\theta)·[\varepsilon_\lambda·B_\lambda(T_s)+(1-\varepsilon_\lambda)·L_\lambda\downarrow]+L_\lambda\uparrow
Lsen=Bλ(Ti)=τλ(θ)⋅[ελ⋅Bλ(Ts)+(1−ελ)⋅Lλ↓]+Lλ↑
式中,
L
s
e
n
L_{sen}
Lsen为星上辐亮度(
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
−
1
W·sr^{-1}·m^{-2}·μm^{-1}
W⋅sr−1⋅m−2⋅μm−1);
B
B
B为普朗克函数;
B
λ
(
T
i
)
B_\lambda(T_i)
Bλ(Ti)是遥感传感器在每个波长
λ
\lambda
λ上所接收到的辐射强度(
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
−
1
W·sr^{-1}·m^{-2}·μm^{-1}
W⋅sr−1⋅m−2⋅μm−1);
T
i
T_i
Ti为通道
i
i
i的亮度温度(星上亮温(
K
K
K));
B
λ
(
T
s
)
B_\lambda(T_s)
Bλ(Ts)是在地表温度为
T
s
T_s
Ts时黑体辐射强度;
T
s
T_s
Ts表示地表温度(
K
K
K);
τ
λ
(
θ
)
\tau_\lambda(\theta)
τλ(θ)波长
λ
\lambda
λ在遥感器视角为
θ
\theta
θ下从地面到遥感器的大气透射率;
L
λ
↑
L_\lambda\uparrow
Lλ↑和
L
λ
↓
L_\lambda\downarrow
Lλ↓为波长
λ
\lambda
λ上的大气上行辐射和大气下行辐射(
W
⋅
s
r
−
1
⋅
m
−
2
⋅
μ
m
−
1
W·sr^{-1}·m^{-2}·μm^{-1}
W⋅sr−1⋅m−2⋅μm−1);
ε
λ
\varepsilon_\lambda
ελ为波长
λ
\lambda
λ上的地表发射率(地表比辐射率)。大多数卫星传感器探测到的光谱带宽的辐射信号是有限的,每个参数的谱段等效值可以通过积分表示为:
X
i
=
∫
λ
1
λ
2
g
i
(
λ
)
X
λ
d
λ
∫
λ
1
λ
2
g
i
(
λ
)
d
λ
X_i=\frac{\int_{\lambda_1}^{\lambda_2}\,g_i(\lambda)X_\lambda{\rm d}{\lambda}}{\int_{\lambda_1}^{\lambda_2}\,g_i(\lambda){\rm d}{\lambda}}
Xi=∫λ1λ2gi(λ)dλ∫λ1λ2gi(λ)Xλdλ
式中,
g
i
(
λ
)
g_i(\lambda)
gi(λ)是通道
i
i
i的光谱响应函数,
λ
1
\lambda_1
λ1和
λ
2
\lambda_2
λ2分别是通道
i
i
i的波长下边界和上边界,
X
X
X代表
B
(
T
)
B(T)
B(T),
ε
\varepsilon
ε,
τ
\tau
τ,
L
λ
↑
L_\lambda\uparrow
Lλ↑,
L
λ
↓
L_\lambda\downarrow
Lλ↓。辐射传输方程作为热红外数据陆表面温度反演的基础,各种温度反演算法的发展都是基于对辐射传输方程的不同假设和近似。
⛄热红外地表温度遥感反演方法
[1]段四波,茹晨,李召良,等.Landsat卫星热红外数据地表温度遥感反演研究进展[J].遥感学报,2021,25(08):1591-1617.
[2]李召良,段四波,唐伯惠,等.热红外地表温度遥感反演方法研究进展[J].遥感学报,2016,20(05):899-920.
[3]肖尧,马明国,闻建光,等.复杂地表地表温度反演研究进展[J].遥感技术与应用,2021,36(01):33-43.
[4]奉澜博.林火多源遥感监测中地表温度反演标准化研究[D].中南林业科技大学,2022.
[5]徐林.多谱段遥感数据地表温度反演方法研究[D].大连海事大学,2023.
| 反演算法 | 特点 |
|---|---|
| 单通道算法 | 对单个红外通道进行建模,需要输入地表发射率、大气传输模型、精确大气廓线。 |
| 多通道算法 | 对多个红外通道进行建模,无需大气廓线数据,反演精度较高,地表发射率具有不确定性,对算法结果影响较大。 |
| 多角度算法 | 根据特定通道在不同角度的亮温差异来消除大气的影响,无需大气廓线数据,数据源稀缺。 |
| 多时相算法 | 基于地表发射率不随时间变化的假设,无需输入地表发射率,结果对传感器噪声、大气校正误差和影像配准精度敏感,现在主要应用于MODIS地表温度反演。 |
| 高光谱反演算法 | 利用地表发射率固有的光谱特征,无需输入地表发射率,需要精确大气校正。 |
| 统计模型 | (单通道回归/多通道回归)算法简单,模型回归需要大量实验数据,模型系数具有较强局地性。 |
| 物理模型 | (微波辐射传输方程/基于发射率求解/基于发射率不变)具有物理意义,且反演精度较经验模型高,过于依赖输入参数和假设条件的准确性。 |
| 神经网络模型 | 方法简单易行,但不具有实际物理意义,通过输入有代表性的训练样本建立数学公式推导结果,对训练样本的依赖性较大。 |
👀单通道算法
单通道算法主要应用卫星单一热红外谱段观测数据,首先假设地表发射率是已知的,然后使用大气廓线数据(即大气透过率、大气下行辐射和大气上行辐射)对大气进行校正,然后,使用大气辐射传输方程结合校正后的大气数据反演得到地表温度。 常用的单通道算法包括:
(1)基于辐射传输方程的算法
该算法是最早发展起来的一种地表温度反演算法。Sobrino等(2004)基于热红外辐射传输方程,去除辐射传输过程中大气对热辐射的影响,从而较为精确地获得地表温度。该算法具有广泛的适用性,能够被应用于任何传感器上的热红外遥感数据。总的来看,基于辐射传输方程的算法不仅具有坚实的物理基础,且计算精度较高。但是该算法计算过程复杂,难以获取实时的大气廓线数据(包括不同高度的温度、湿度等)。而使用标准大气廓线数据替代实时的大气廓线数据则会影响大气对地表辐射的模拟,从而降低地表温度的反演精度。
(2)单窗算法
为了减少对大气廓线的依赖,Qin等(2001)通过引入大气平均作用温度,提出了一种基于Landsat 5 TM第6波段数据的单窗算法。该算法将大气和地表的影响直接包含在反演公式中,只需要大气平均作用温度和大气透过率两个大气参数,估算得到地表温度。总的来看,单窗算法既考虑了地表比辐射率的影响,也考虑了大气辐射的影响。在地表温度反演过程中所需要的大气参数比传统的辐射传输方程要少,且反演精度较高,普适性较强。
(3)普适性单通道算法
Jiménez-Muñoz和Sobrino(2003)针对Landsat5 TM数据提出一种反演地表温度的普适性单通道算法。该算法假设地表比辐射率已知,根据辐射传输方程对普朗克函数进行一阶泰勒级数展开,仅需通过大气水汽含量反演地表温度。JiménezMuñoz等(2009)对普适性单通道算法进行改进,并扩展到Landsat4、5 TM和Landsat7 ETM+。Jiménez-Muñoz等(2014)和Cristóbal等(2018)提出了针对Landsat 8 TIRS数据的单通道算法。总的来看,普适性单通道算法既考虑了地表比辐射率的影响,也考虑了大气辐射的影响,适用于任何带宽约为1 μ m μm μm的热红外传感器,并且因为其需要的实时大气参数较少而被广泛使用。
(4)实用单通道算法
针对现有单通道算法中线性化普朗克函数和大气参数系数求解引入的误差,Wang等 (2019)提出了实用单通道算法PSC(Practical SingleChannel)。实用单通道算法直接构建地表黑体辐射亮度与星上辐射亮度之间的关系,避免线性化普朗克函数带来的误差。通过分析大气参数构建最优大气参数估算模型,并基于全局拟合方法求解大气参数模型的系数,规避多个大气参数误差的叠加。实用单通道算法包含两种形式:①基于大气水汽含量的实用单通道算法 ;②基于大气水汽含量和近地表气温的实用单通道算法。实用单通道算法对输入参数误差的敏感性比普适性单通道算法弱,具有更好的稳定性;与普适性单通道算法相比,实用单通道算法地表温度反演精度提升了0.47 K K K。
需要注意的是,单通道算法是对辐射传输方程的简单变形,前提是地表发射率和大气廓线已知。这些方法虽然在理论上能够精确反演地表温度,但高精度的地表发射率在实际应用中很难获取。
👀多通道算法
(1)昼夜法
昼夜法是专门为MODIS传感器研发的反演地表温度的算法。该算法利用MODIS七个热红外通道分别在白天和夜间观测到的数据获取地表发射率,然后利用分裂窗算法反演地表温度。该算法是针对MODIS传感器开发的,在其他传感器中应用较少。其反演精度可保证在0.5 K K K之内,最大误差为3 K K K。目前,该算法己成为MODIS温度产品的官方算法之一。
(2)温度/发射率分离法(Temperature/Emissivity Separation, TES)
温度发射分离法是Gillespie A.等人根据Terra ASTER 5个热红外波段的特点,专门提出的一种温度发射率分离算法,但使用TES算法会造成由于波段间高度相关性引起的不稳定问题。张猛在其文中已详细地描述了目前己经发展的各种TES算法。相关数值模拟实验表明,该算法的温度反演精度为±1.5 K K K,地表发射率的反演精度为±0.015,该算法已经成为ASTER温度产品的官方算法。
👀分裂窗算法
劈窗算法也称分裂窗算法,主要是利用在一个大气窗口内具有不同大气吸收特性的两个相邻热红外通道表面的不同线性组合来消除大气影响,反演地表温度。该算法是目前热红外遥感反演地表温度中最成熟、最精确的地表温度反演算法。
- 基于NOAA/AVHRR数据的劈窗算法
- 基于MODIS/TERRA数据的劈窗算法
- 基于FY-4A/AGRI数据的劈窗算法
- 基于Himawari-8/AHI数据的劈窗算法
- 基于Landsat-8/OLI-TIRS数据的劈窗算法
详细的劈窗算法技术流程,大家可以调研相关论文进行学习。
👀多角度算法
多角度算法是建立在同一物体由于从不同角度观测时所经过的大气路径不同而产生的大气吸收不同的基础上。由于大气吸收体的相对光学物理特性在不同观测角度下保持不变,大气透过率仅随角度的变化而变化。与分裂窗算法的基本原理类似,大气的作用可以通过特定通道在不同角度观测下所获得亮温的线性组合来消除。这种算法主要基于第一代双角度模式卫星,即搭载在第一代欧洲遥感卫星(ERS-1)上的沿轨扫描辐射计(ATSR)发展而来。双角度算法应用于卫星数据时有几个实际困难:
-
多角度算法中的一个重要现象是发射率的角度相关性,因为在卫星空间分辨率尺度下,自然地表的角度效应是未知的,如裸土和岩石。
-
地表温度的角度相关性也是一个问题。除了需要大气晴空无云并且水平均一,还必须要求在不同斜程路径下的多角度测量有明显差异。否则,不同角度下的测量会高度相关,导致算法不稳定,并对仪器噪声极其敏感。
-
在不同观测角度下对同一目标地物进行观测会覆盖不同的传感器区域(即像元)。即使可能会观测到同样的像元大小,但由于地物的3维结构,在不同观测角度下观测到的地物仍可能明显不同。
-
不同观测角度像元的配准不好会导致地表温度反演结果的巨大误差。
所以,多角度算法仅适用于理想大气条件下的均质区域(如海洋表面或浓密森林植被),而不适用于非均质地表。
👀多时相算法
多时相算法是在假定地表发射率不随时间变化的前提下利用不同时间的测量结果来反演地表温度和发射率的,比较有代表性的是两温法(Watson,1992)和日夜双时相多通道物理反演法(Wan和Li,1997)。
(1)两温法
两温法的思路是通过多次观测来减少未知数的个数。假设热红外通道已经经过精确的大气校正并且发射率不随时间而发生变化,那么如果地表被N个通道两次观测,2N次测量将会有N+2个未知数(N个通道的发射率以及2个地表温度)。因此,当N≥2时,这N个地表发射率和2个地表温度可以从2N个方程中同时得到(Watson,1992)。注意到地表发射率不随时间而变化的假设暗示地表是均匀的并且有相对稳定的土壤湿度,所以首先是要减小由于像元大小和观测角度带来的地表发射率的变动,其次要避免地表发射率随土壤湿度的变化而变化,比如要考虑降雨和露水的发生。两温法的主要优势是它对地表发射率的光谱形状没有作出假设,只是假定发射率是不随时间而变化的。存在的问题如下:
-
虽然这一方法有一个简单直接的公式,但是由于这2N个方程是高度相关的,因此方程的解可能不稳定,并且对传感器噪声和大气校正产生的误差非常敏感(Caselles等,1997;Gillespie等,1996;Watson,1992)。
-
由于在没有实测大气廓线数据的情况下,很难进行非常精确的大气校正,因此在反演地表温度和发射率时使用近似的廓线可能导致比较大的误差。
-
Peres和DaCamara(2004)发现增加观测的次数和(或)温差可以提高反演的精度,但是这种提高会受到热红外测量高相关性的限制。
-
这一方法还需要在两个不同的时间点对影像进行精确的几何配准(Gillespie等,1996;Watson,1992)。对于下垫面均匀的区域,不精确配准带来的地表温度和发射率误差较小,但对于下垫面不均匀的区域,这一误差将较大(Wan,1999)。
-
卫星观测天顶角的改变会引起地表发射率的改变,因此违背了地表发射率不随时间改变的假设,导致两温法的精度降低(Li等,2013)。
(2)日夜双时相多通道物理反演法(昼夜法)
Wan和Li(1997)受到日夜温度无关波谱指数法和两温法的启发,进一步提出了日夜物理反演法,即通过结合白天和晚上的中红外以及热红外数据来同时反演地表温度和发射率。这一方法假定从白天到夜晚地表发射率不会发生太大的改变,并且在中红外波段感兴趣范围角度形式因子的变化很小(<2%),以此减少未知数的个数,从而使反演更加稳定。通常来讲,日夜物理反演法是之前提到的使用两次观测的两温法的发展,与之前提到的两温法和日夜温度无关波谱指数法相比,日夜算法在以下几个方面较为突出:
-
对于中红外通道,白天太阳辐射的存在会显著地减小方程之间的相关性,从而使方程的解更加稳定和精确。
-
通过考虑初始大气廓线带来的误差,引入两个变量(大气底层的空气温度: T a T_a Ta、大气水汽含量: W V WV WV)后,地表温度和发射率的反演精度得到很大的提高。
-
日夜算法不需要12小时间隔的测量(白天和夜晚),只要地表发射率不发生大的改变,几天内获得的白天和夜晚的数据也同样可用。
但是,和其他的多时相反演方法类似,日夜算法同样面临着几何配准精度低以及观测天顶角变化等关键问题。
👀高光谱反演算法
高光谱反演算法依靠的是地表发射率固有的光谱特性而不是时相信息,其中比较有代表性的是迭代光谱平滑温度发射率分离法(Borel,2008)和线性发射率约束法(Wang等,2011)。在一些合理的假设和约束下,通过减少未知数的个数或者增加方程的数量,利用这些方法可以使用经过大气校正后的辐射值反演出地表温度和发射率。
⛄复杂地表温度反演的局限性
(1)病态反演问题
无论是热红外辐射传输模型还是被动微波传输模型,反演过程始终是个病态问题,即方程未知数个数总是比方程个数多。因此在反演过程中,各种模型的建立都基于一定的约束条件和假设,使方程可解。但是约束方程和条件不确定性往往是反演算法的重要误差来源。
(2)地表复杂性
相比平坦均一的地表,山区地形更为复杂,景观破碎度和空间异质性更强,对地表发射率的估算带来更大困难。
- 复杂的地形对土壤物理性质、水分分布和地表植被类型存在影响。①不同土壤类型对辐射的吸收、反射、透射不同,影响地表能量通量变化和地表发射率、反射率和吸收率;②山地水分分布受地形和海拔高度的影响,地表起伏使气流抬升或下沉,山体遮挡阻止水汽移动,使山地地表水分的水平和垂直方向分布表现出异质性。地表水分分布不均,影响土壤湿度和植被生长,同种土壤或同种植被可能有不同的发射率;③植被对地表温度有冷却和保温的作用,可以抑制地表温度剧烈改变,现有地表发射率的估算多基于地表植被与土壤比例或植被覆盖度分级阈值,对于植被类型丰富、地形起伏的复杂地表,以单一的发射率估算方法不能有效解决发射率精度问题。复杂地表区域,下垫面破碎,水分、土壤和植被复杂多变,因子间相互影响,由此地表发射率的估算必须考虑环境因素。输入参数多源且不确定性大,是复杂地表地表温度反演难度大的主要影响因素。
- 山区地表具有复杂三维结构,热辐射与地表存在复杂的相互作用。研究山区热辐射传输过程,必须考虑地表方向性,近年来国内外专家学者构建了许多热红外模型,包括辐射传输模型、几何光学模型、3D模型、混合模型和参数模型等。模型的发展需要考虑方向性、地形因素和热力因素,目前的模型多建立于条件可控的实验场或小区域试验区,应用于复杂多变的山区地表温度建模仍存在着挑战性。在坡度、坡向和地形不断变化和相互遮蔽的山区,地表接收到的太阳入射辐射能量,包括直接辐射、散射辐射和邻近地形的反射辐射,辐射间差异显著。坡度、坡向和地形直接影响地表辐射的分布,地形的遮蔽作用同样使温度在空间分布上存在差异。对山地热辐射建模,不仅需要考虑复杂的地形因素,还需要考虑能量平衡和流体力学等影响。山地地形条件直接影响地表辐射收支和能量平衡,提高复杂地区地表温度反演精度,还需要进一步建立统一且普适性强的模型。提高山区地表温度反演精度,需要考虑地形因素对发射率的影响、邻近效应、能量平衡等,优化复杂地表辐射传输模型、动力模型、核驱动模型,并结合地面多角度观测数据对模型进行修订。
(3)水汽与云的影响
水汽是大气中重要的吸收气体,其吸收系数与频率、大气温度、大气压强和水汽密度相关,并在时间空间上都有很大变化。云中包含液态水和各种微粒能吸收和散射辐射。当天空晴朗无云时,消光系数主要是水汽和氧气的吸收,在云雨天气,云的存在致使热红外信号失真,使用热红外反演方法无法获取地面温度信息。微波虽然能穿透云层,但是在云中传播还应考虑到液态水的瑞利散射。云覆盖区下不同地表类型,云对其有不同程度的影响;对于像元的位置而言,位于云边缘像元影响程度小于位于云覆盖中心的像元;云覆盖时间越长,对地表温度影响越大;云阴影与云遮挡的地区,云覆盖对其影响也不一样。现有的地表温度反演算法主要是针对晴空像元,云下地表温度反演仍是一个难题。水汽和云是复杂地表温度反演重要障碍,热红外波段的重建、对不同厚度云像元的识别、云遮挡区域数据填补等问题还有待进一步深入研究。
(4)真实性验证的不确定性
遥感反演的真实性检验,包含对算法可行性和精度进行检验,对温度产品的精度、稳定性、适用性、生产效能进行检验,以及算法应用是否满足地球科学应用需求的检验。对于地形复杂、地表破碎的复杂地表区域,反演的温度像元与地面观测值存在尺度差异,单个像元值难以反映地面实际状况,有效的检验方法和尺度转换是提高检验可信性的基本要求。目前用于复杂地表的地表温度检验方法还是常规地表温度真实性检验方法,主要有基于温度方法、基于辐射的方法、交叉验证以及时间序列分析4种典型的检验方法。
| 检验方法 | 参考对象 | 适用范围 | 特点 |
|---|---|---|---|
| 基于温度检验 | 地表实测温度 | 下垫面均一,地势平坦地区 | 简单直接,对站点数据质量要求高,不适用于无站点和地物破碎区域 |
| 基于辐射检验 | 辐射传输方程模拟辐射值 | 无地面监测站点地区 | 需要输入实测大气廓线和地表发射率,复杂地表区域参数获取困难 |
| 交叉验证 | 设为真值的温度产品 | 无实测温度和模拟参数情况 | 对参考产品要求高,山区和云覆盖区产品精度无保证;产品匹配问题影响验证结果 |
| 时间序列验证 | 目标物长序列变化 | 传感器本身监测 | 传感器运行时间较长,对异常值敏感,不适用于地表温度检验 |
地表温度真实性检验方法不断被改进,并在复杂地形区开展应用,但是仍存在以下问题:①空间异质性问题,地表破碎区同温像元内部存在较大差异,缺少绝对均一的地表,真实性检验标准存在不确定性。②辐射方向性问题,复杂地表地物多样,地势起伏,地表方向亮温角度差异大,制约地表温度反演精度和长波估算精度。③时空、角度不匹配问题,卫星数据反演的地表温度是卫星过境的瞬时温度,而地面是不断变化的,参考值和比较值间存在着差异性,尤其是对站点分布少的山地区域,得到与卫星过境同时段的高质量观测值更加困难。④仪器观测不确定性,仪器获取数据存在不确定性,站点的布设不均一。复杂地表区域站点数过少,山地区域仪器维护困难,数据质量和参数完整性不能得到有效保障。
多谢!多谢!
笔者不才,请多交流!!!
欢迎大家关注预览我的博客Blog:HeartLoveLife
能力有限,敬请谅解!!





![[力扣题解]102.二叉树的层序遍历](https://img-blog.csdnimg.cn/direct/d7964db06551417b81720b617de34a1b.png#pic_center)