继续学习

一、判断链表是否带环

141. 环形链表 - 力扣（LeetCode）

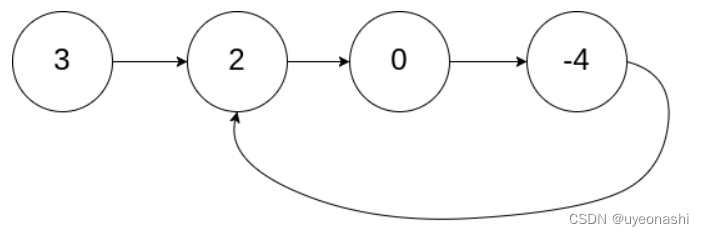
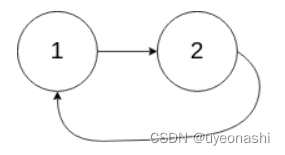
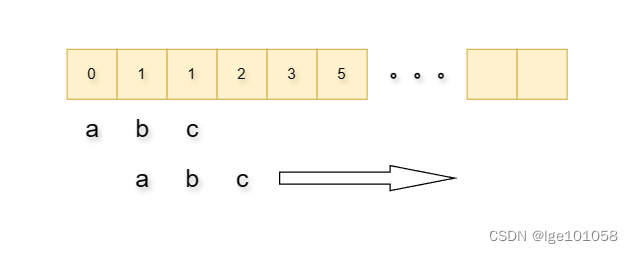
思路：用快慢指针，快指针走两步，慢指针走一步，当慢指针走一半快指针进到环里

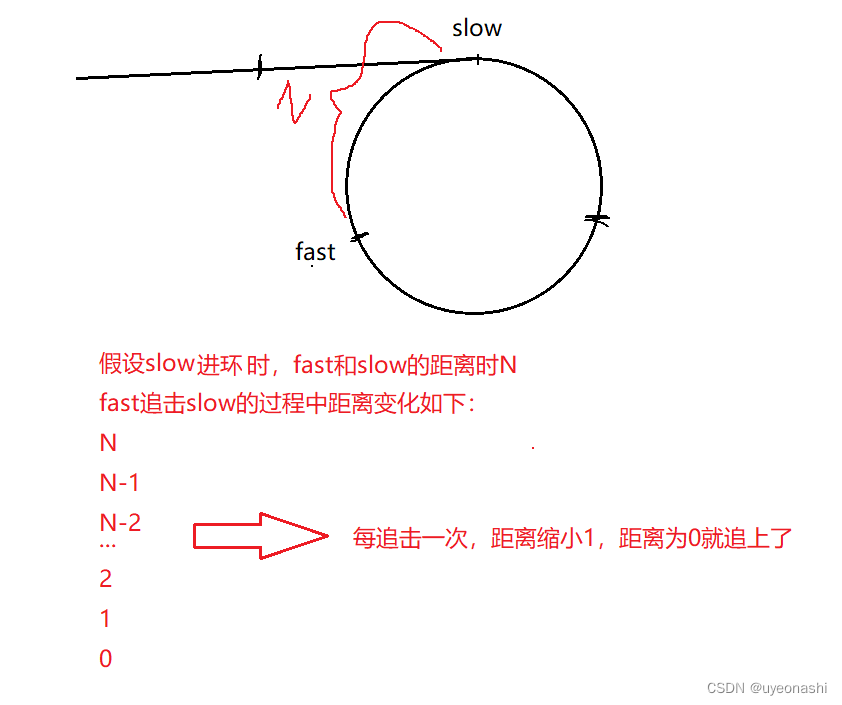
           当慢指针进环，快指针已经在环中转了一会儿了

      | |     

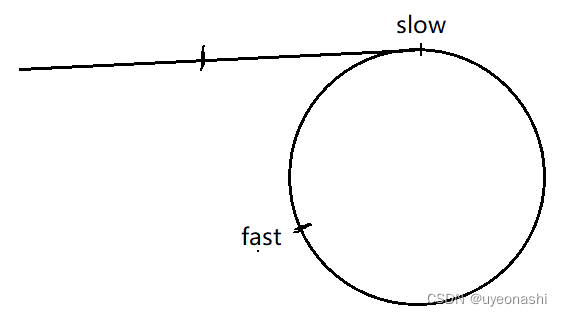
当慢指针进环，快指针就开始追击， 快指针如果追上慢指针就带环

如果不带环，慢指针走一半，快指针就走完了

代码如下：

 typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
    ListNode *slow = head;
    ListNode *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        return true;     
    }
    return false;
}

二、拓展

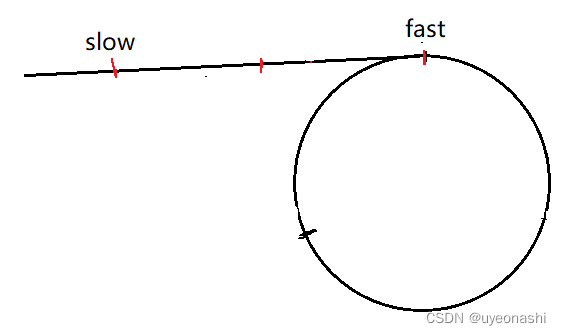
2.1、为什么一定会相遇，有没有可能会错过？

2.2.slow一次走一步，fast一次走3步，4步，5步，N步行不行？

这里我已fast走三步为例，当slow进环的时候，fast已经在环中转了一会儿了，还是追击问题

---

我们假设当slow指针刚进入环的时候与fast指针相差N步，由于此次fast指针每次走3步，也就意味着fast相对于slow的速度是2，就是说fast每走一次与slow的差距就会减少两步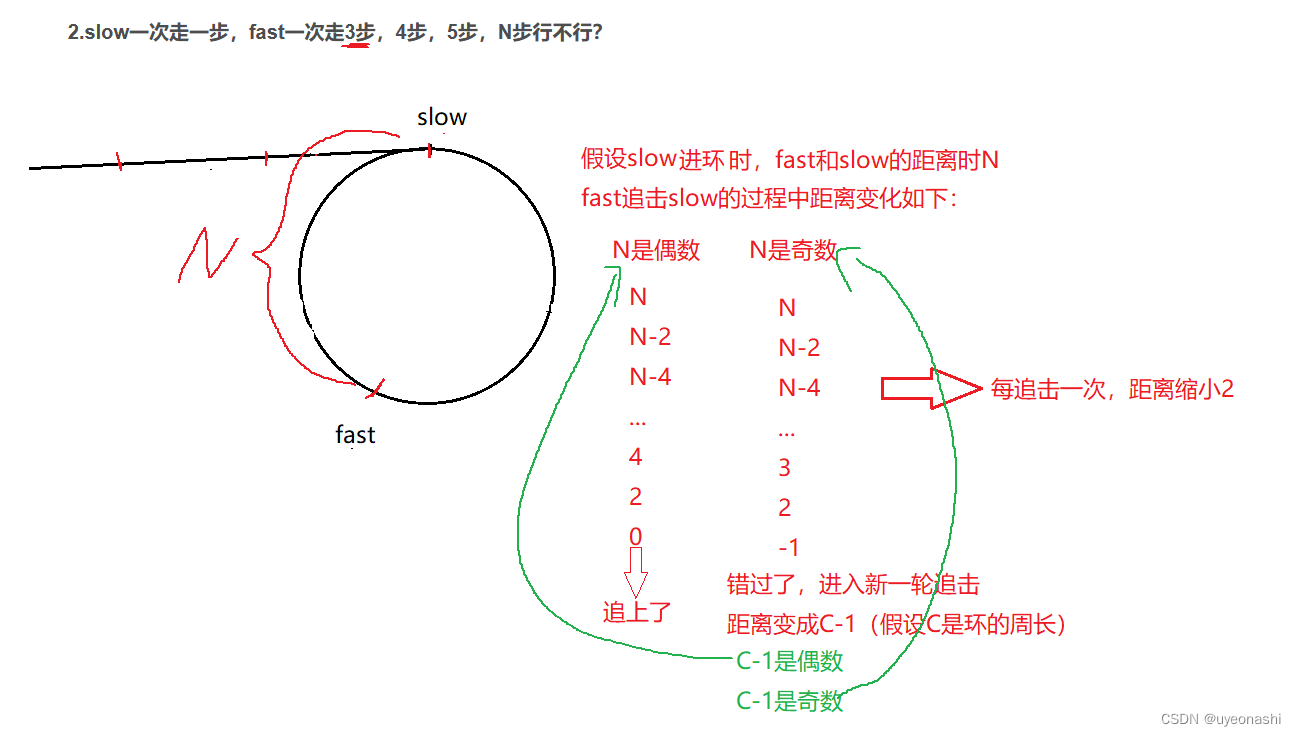

会出现上述的两种情况，

第一种情况：fast与slow最终相差0步，证明fast与slow可以相遇。

第二种情况：最终fast与slow相差-1步，就是说fast反超slow了，此时进入到新一轮的追击问题了，他们相差的步数为（假设圆圈的周长为C）C-1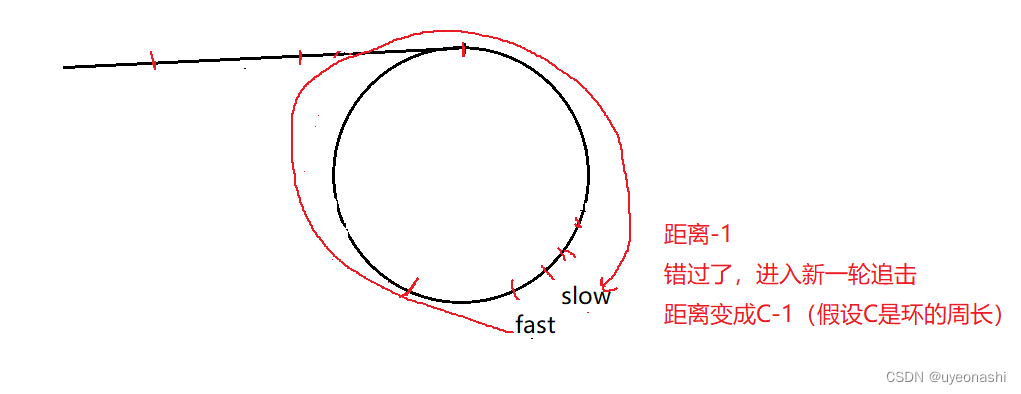

如果C是一个奇数那么C-1就为偶数，那么最终fast就会与slow相遇。
如果C是一个偶数那么C-1就为奇数，就会导致fast永远不会与slow相遇，是一个死循环

总结：1、N是偶数，第一轮就追上

           2、N是奇数，第一轮就会错过，距离变成C-1

                a、如果C-1是偶数，下一轮就追上

                b、如果C-1是奇数，那么永远追不上

2.3 永远追不上的条件存在吗？

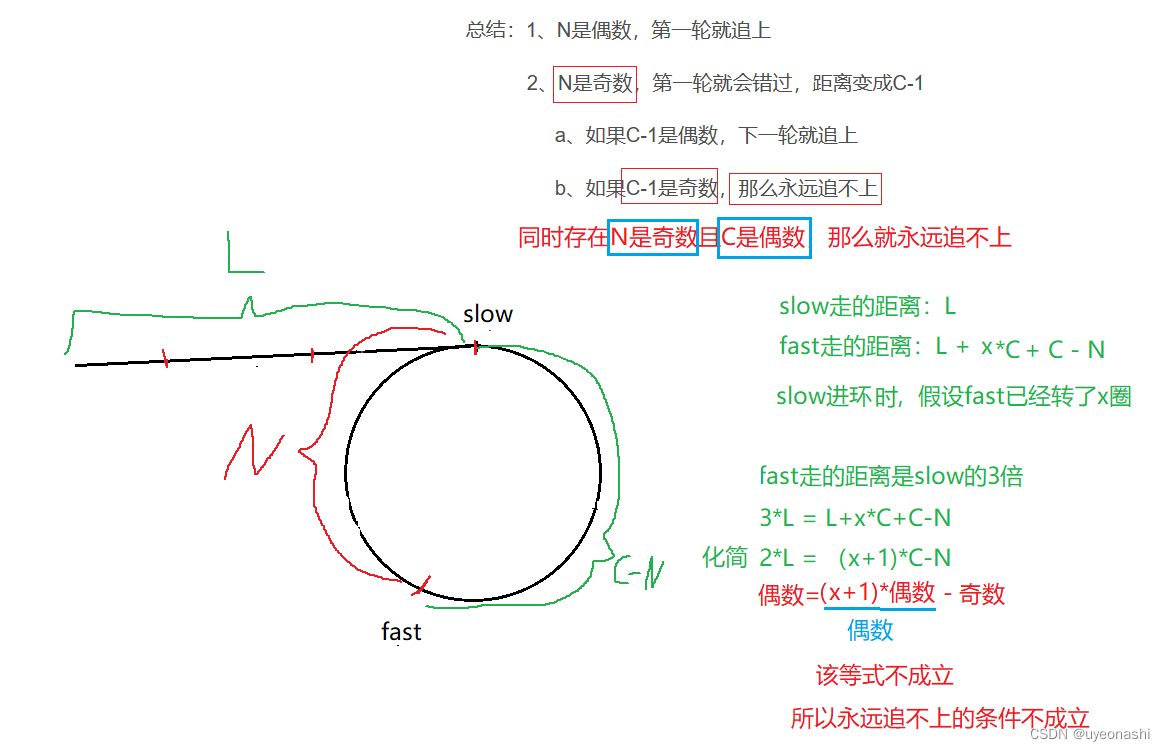
结论：一定能追上，N是偶数第一轮就追上，N是奇数第一轮追不上，C-1是偶数第二轮就能  追上

看到这里是不是有一部分小伙伴就要迷茫了，上面不是说追不上了吗，怎么有追上了，那么从数学方面分析是不是会简单一些呢？

可以将（N是奇数时，C也是奇数；N是偶数时，C也是偶数）带入到2.2的图中去反证

---

本篇到此结束，可以自己下去画一画，想一想，如有问题欢迎在评论区指正。