一、学习目标

1. 理解深度学习的基本概念和原理：学习深度学习的起源、发展历程以及核心思想，理解神经网络、反向传播、优化算法等基本概念和原理。
2. 掌握深度学习的基础知识和技术：包括线性回归、多层感知机、卷积神经网络（CNN）、循环神经网络（RNN）等深度学习模型的基本原理和实现方法。
3. 培养动手实践能力：通过大量的编程实践，让读者能够亲自构建、训练和评估深度学习模型，从而加深对深度学习技术的理解和掌握。
4. 提升问题解决能力：结合具体的案例和项目，培养读者运用深度学习技术解决实际问题的能力，如图像识别、语音识别、自然语言处理等。
5. 培养批判性思维和创新能力：在学习的过程中，读者需要不断思考、分析和总结，从而培养批判性思维和创新能力，为未来的研究和应用打下坚实的基础。
6. 了解深度学习的前沿技术和应用：介绍深度学习领域的最新研究成果和应用案例，让读者了解深度学习技术的发展趋势和应用前景。

二、环境搭建

• 安装Anaconda，注意选择合适版本，先查看版本 nvidia-smi

• 安装GPU版本的Tensorflow和Pytorch

• 作者的显卡驱动 511.23
  

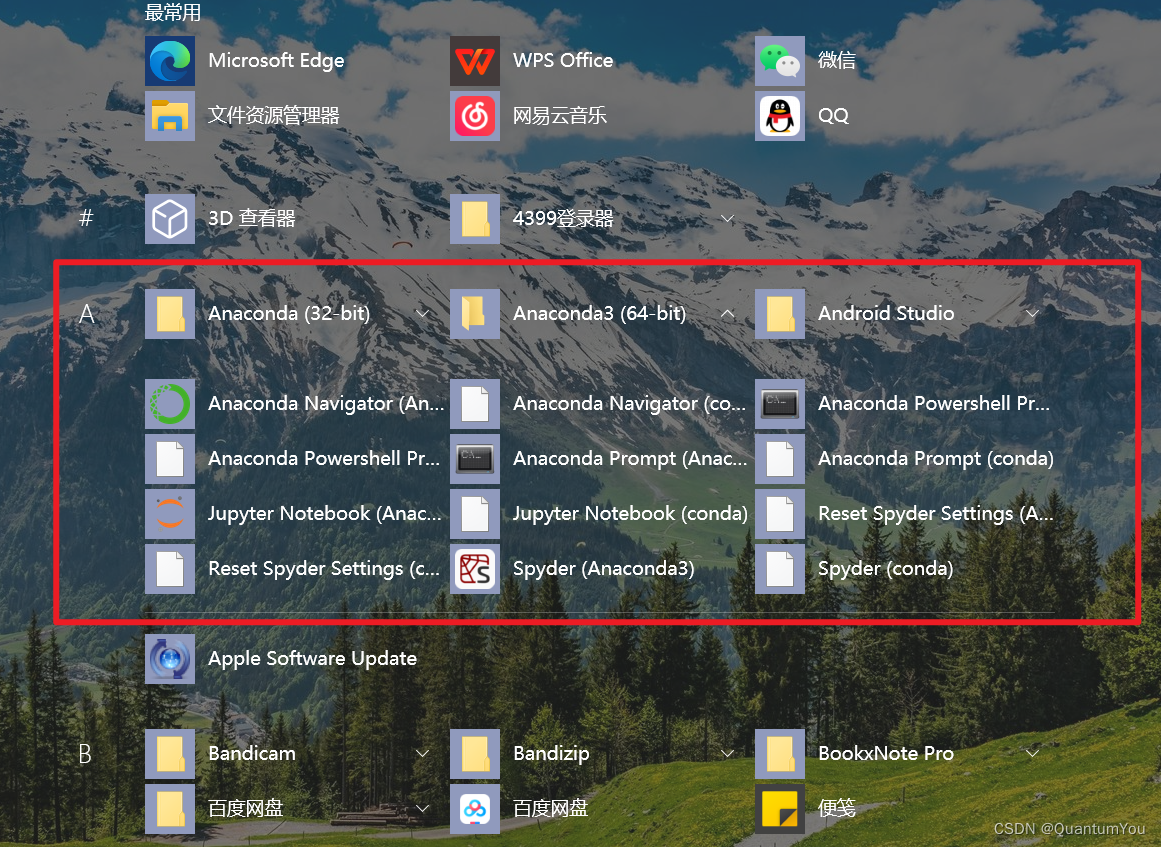
技巧：可以借助图形化Navigator工具，查看安装内容和开发环境等

安装Pytorch

pip install torch torchvision -i http://mirrors.aliyun.com/pypi/simple/  --trusted-host mirrors.aliyun.com
pytorch jingxiang

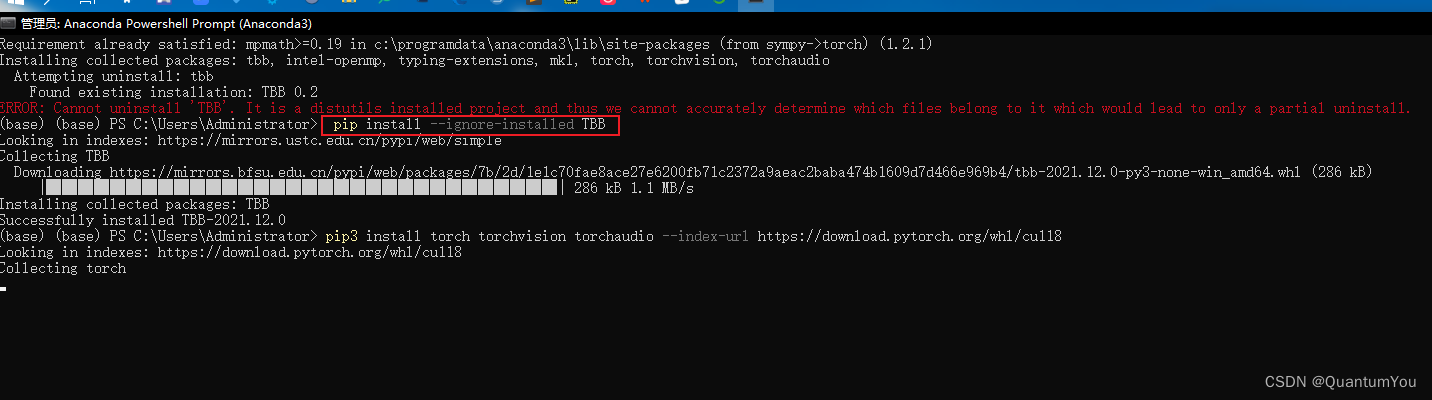
GPU 版tensoflow 安装

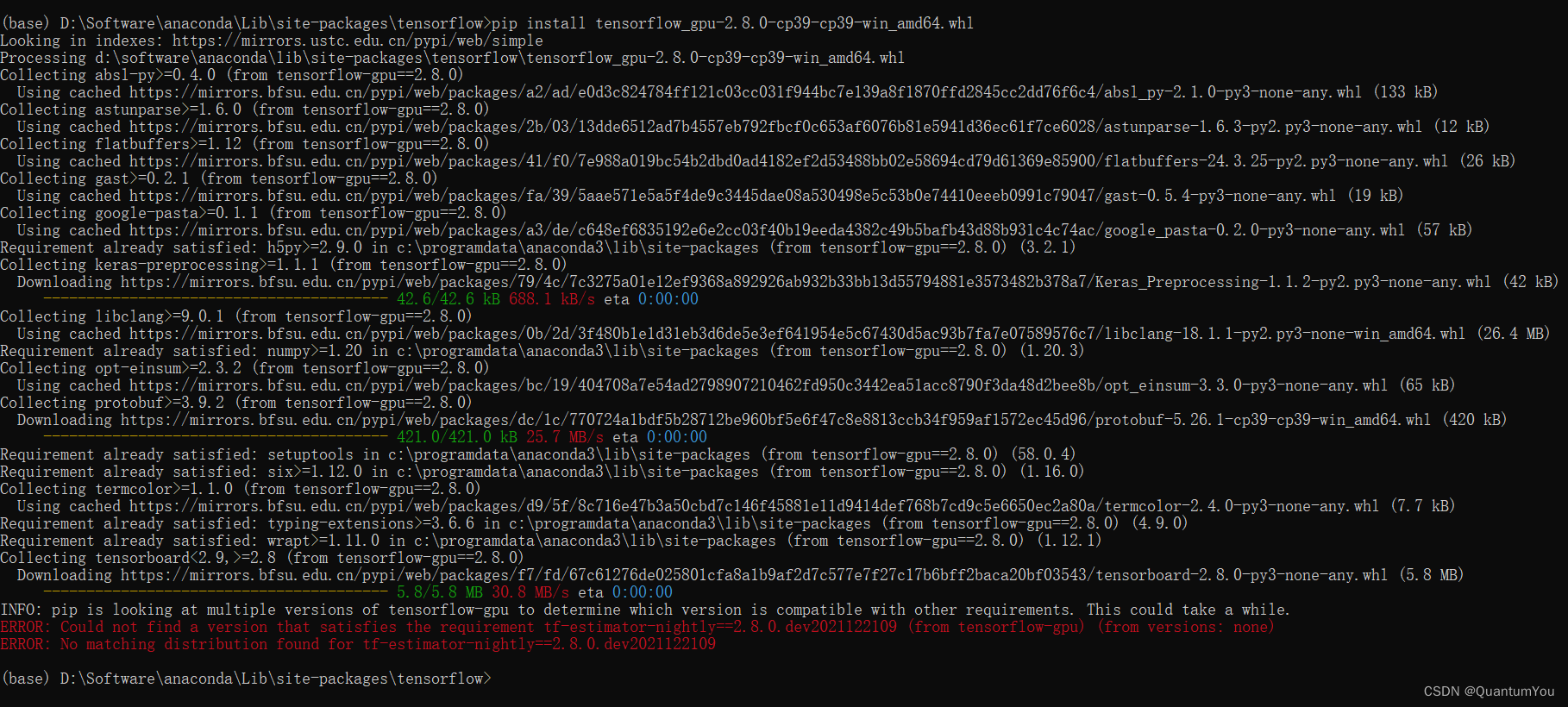
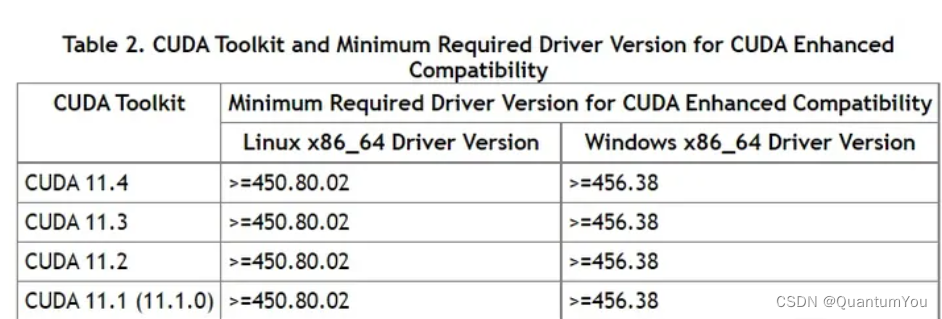
• 注意这里有个大坑要！🔥 要选择对应的版本

• 版本对应表

• GPU tensorflow
  
  

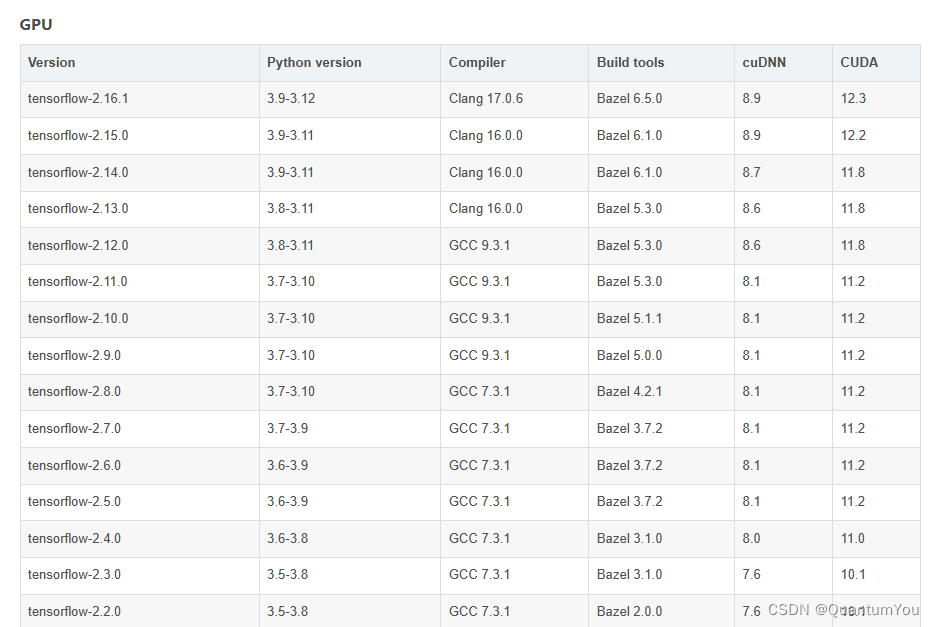
• 测试成功 成功安装GPU 版本🚀

• 可以在可视化工具中的环境里查看安装的插件（脚本）

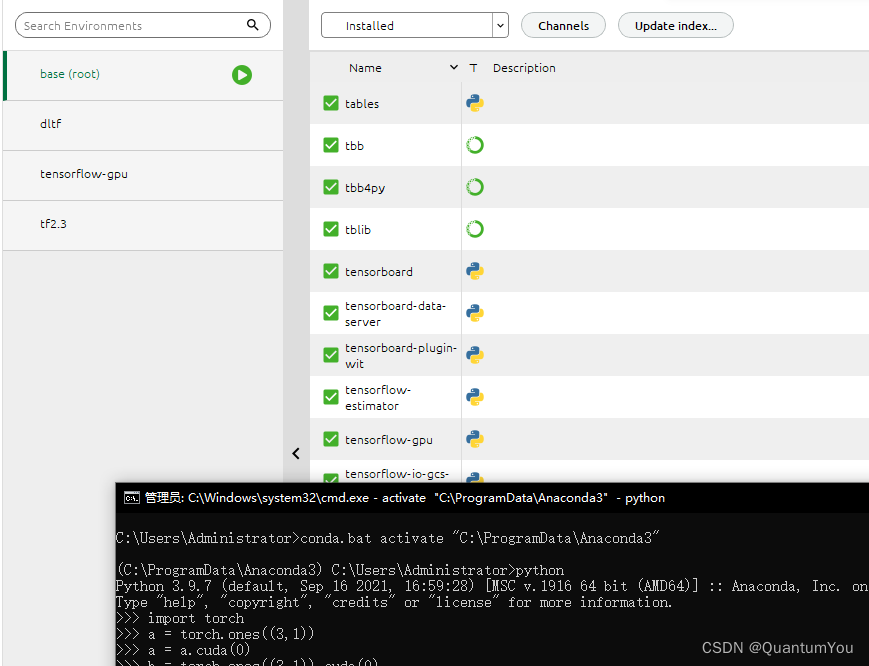
解决Jupyter notebook找不到内核的问题

①在prompt 中进行搭建

②输入pip install jupyter d2l 安装d2l 或者把原文件直接放在目录下

③解决 No module named 'd2l' 的问题

④最后 jupyter notebook 启动！！🚀

• 正在训练

三、数据操作

建议参考官方文档 如下⬇️

https://zh.d2l.ai/chapter_preliminaries/index.html

数据类型介绍

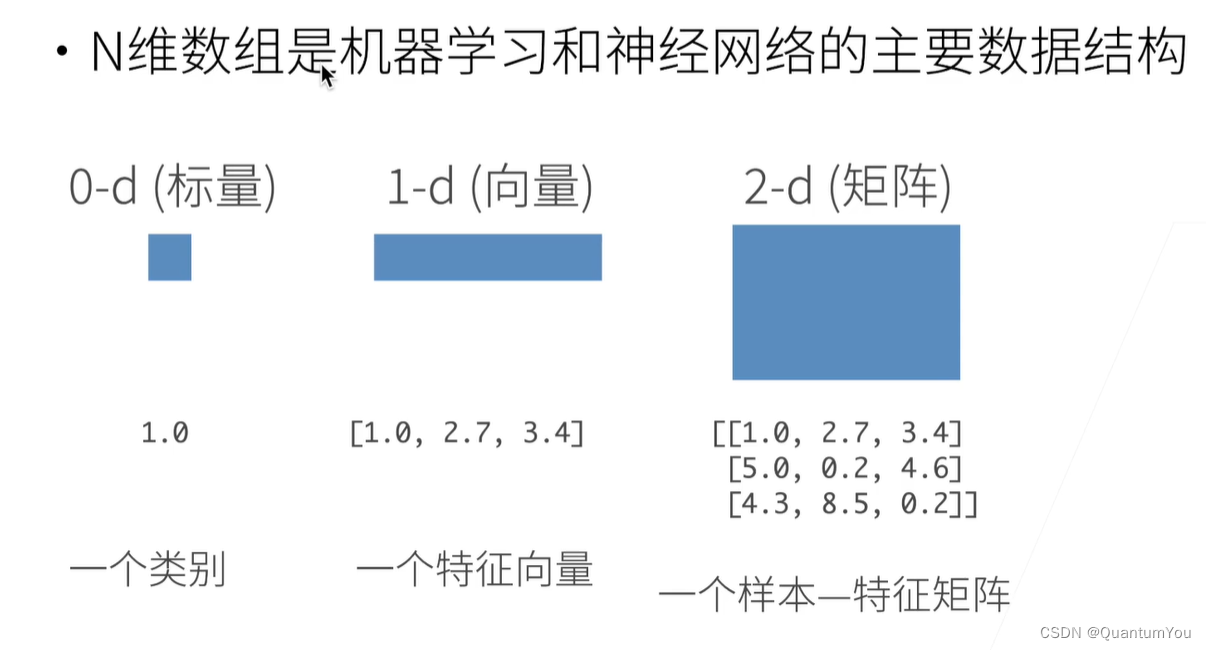
• 左闭右开区间，每三行一跳，每二列一跳

1、张量介绍

张量表示一个由数值组成的数组，这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量（vector）； 具有两个轴的张量对应数学上的矩阵（matrix）； 具有两个轴以上的张量没有特殊的数学名称。

首先，我们可以使用 arange 创建一个行向量 x。这个行向量包含以0开始的前12个整数，它们默认创建为整数

• numel 是一个函数，用于计算数组（或矩阵）中的元素总数

[要想改变一个张量的形状而不改变元素数量和元素值，可以调用reshape函数。]
例如，可以把张量x从形状为（12,）的行向量转换为形状为（3,4）的矩阵。
这个新的张量包含与转换前相同的值，但是它被看成一个3行4列的矩阵。

元素赋值

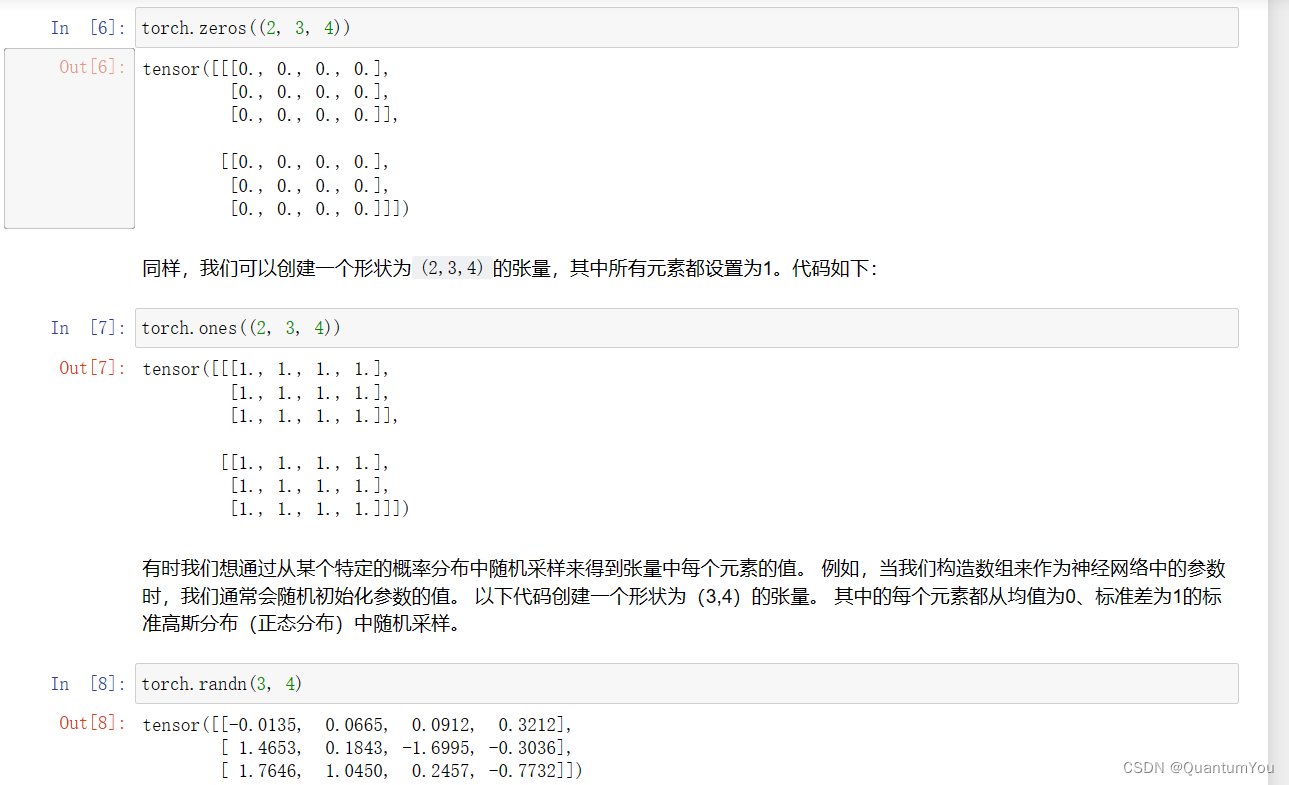
还有很多函数可以创建Tensor， 下表给了一些常用的作参考。

函数	功能
Tensor(*sizes)	基础构造函数
tensor(data,)	类似np.array的构造函数
ones(*sizes)	全1Tensor
zeros(*sizes)	全0Tensor
eye(*sizes)	对角线为1，其他为0
arange(s,e,step)	从s到e，步长为step
linspace(s,e,steps)	从s到e，均匀切分成steps份
rand/randn(*sizes)	均匀/标准分布
normal(mean,std)/uniform(from,to)	正态分布/均匀分布
randperm(m)	随机排列

2、运算符介绍

x**y 是求幂

• dim 在第0维合并

• dim 为0按行 dim为1按列

• torch.cat 是 PyTorch 中的一个函数，用于将多个张量（tensors）沿着指定的维度进行连接（concatenate）。连接操作是将多个张量在指定的维度上“堆叠”在一起，形成一个新的张量。

下面的例子分别演示了当我们沿行（轴-0，形状的第一个元素） 和按列（轴-1，形状的第二个元素）连结两个矩阵时，会发生什么情况。
我们可以看到，第一个输出张量的轴-0长度（ 6 ）是两个输入张量轴-0长度的总和（ 3+3 ）； 第二个输出张量的轴-1长度（8）是两个输入张量轴-1长度的总和（ 4+4 ）。

3、广播介绍

• 这种需要维度两同，且两个变量分别有一个是一维的，否则也不能相加
  

4、索引和切片

[可以用[-1] 选择最后一个元素，可以用[1:3]选择第二个和第三个元素]：

• 在PyTorch中，X[0:2, :] = 12 这行代码的意图是尝试将张量 X 中从第0行到第1行（不包括第2行）的所有列的值设置为12

5、节省内存

• id 类似于C语言中指针的功能

• 在Python中，当使用 id() 函数时，得到的是对象在内存中的“身份”或“地址”的整数表示。但是，当对对象执行某些操作时，如加法（在支持加法的对象上，如整数、浮点数、列表、张量等），这通常会导致Python创建一个新的对象来存储结果，而原始对象保持不变。

• 在PyTorch中，张量通常包含两部分：一个指向底层数据结构的引用和一个描述张量形状、数据类型等属性的头部。执行 Z[:] = X + Y 时，实际上是在原地（in-place）修改了 Z 指向的底层数据，而没有创建新的张量对象。

在PyTorch中，torch.tensor 用于创建一个张量（tensor）。 a = torch.tensor([3.5]) 创建了一个包含单个元素（浮点数3.5）的一维张量。

1. a: 这是创建的原始张量，它是一个PyTorch张量对象，包含一个浮点数3.5。

print(a)
# tensor([3.5000])

2. a.item(): 当有一个只包含一个元素的张量（且该元素是数值类型，如整数或浮点数）时，可以使用 .item() 方法来提取这个元素并将其作为Python的数值类型（在这个例子中是浮点数）返回。

print(a.item())
# 3.5

3. float(a): 这里有一个常见的误解。不能直接将PyTorch张量转换为Python的 float 类型，因为 float() 函数期望其参数是一个可以转换为浮点数的Python数值或可以转换为浮点数的对象（如整数或字符串表示的数字）。尝试 float(a) 时，会得到一个错误，因为PyTorch张量不是Python的数值类型。

# print(float(a))  # 这会抛出一个错误

4. int(a): 同理，int() 函数也不能直接用于PyTorch张量。它会尝试将其参数转换为一个整数，但PyTorch张量不是可以直接转换为整数的类型。

# print(int(a))  # 这也会抛出一个错误

但是，如果知道张量 a 只包含一个元素，并且想将这个元素转换为整数（尽管这可能会导致精度损失，因为浮点数被截断为整数），可以这样做：

print(int(a.item()))
# 3

这里，我们首先使用 .item() 方法将张量 a 的元素提取为一个浮点数，然后将其转换为整数。

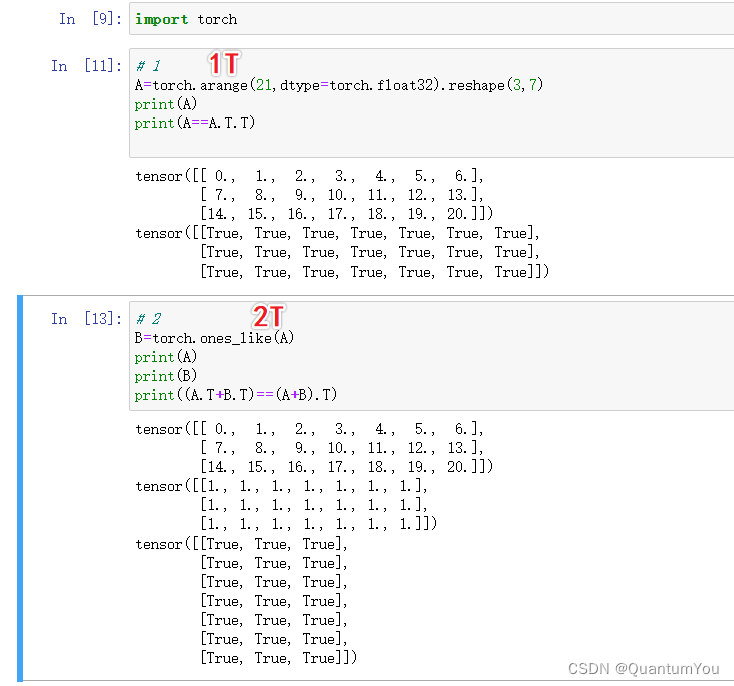
6、课后练习实现 🔥

• 运行本节中的代码。将本节中的条件语句 X == Y 更改为 X < Y 或 X > Y，然后看看可以得到什么样的张量。
• 用其他形状（例如三维张量）替换广播机制中按元素操作的两个张量。结果是否与预期相同？
  

import torch
#1 均返回与X、Y同型矩阵，矩阵元素是bool型

A=torch.tensor([[1,2,3,4],[1,3,4,5]])
B=torch.tensor([[1,3,2,1],[1,4,3,5]])
print(A,'\n',B,'\n',A==B,'\n',A<B,'\n',A>B)

• 想要广播，每个轴必须至少有一个张量是1个元素的，否则无法复制！！！
  

C,D=torch.ones(1,3,1),torch.ones(4,1,2)#可广播
C+D
print((C+D).shape,C+D)

四、数据预处理

1、读取数据集

• CSV(Comma-Separated Values) 是一种简单的文件格式，用于存储表格数据（如电子表格或数据库）。CSV 文件通常由一系列的行组成，每行又由字段组成，字段之间由分隔符（通常是逗号）分隔。CSV 文件通常不包含列名，但也可以包含，特别是在第一行作为标题行。

Name,Age,City
John Doe,30,New York
Jane Smith,25,
Los Angeles Bob
Johnson,45,Chicago

• NA=Not Applicable, NaN=Not a Number

首先我们先造个数据🐱

import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

2、处理缺失数据

使用Python的pandas库来处理一个名为data的DataFrame。下面是对这段代码的详细解释：

1. 数据选择：

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]

* `data.iloc[:, 0:2]`：使用`.iloc[]`索引器选择`data` DataFrame中的前两列。这里，`:`表示选择所有的行，`0:2`表示选择从索引0（包括）到索引2（不包括）的列，即选择第一列和第二列。
* `data.iloc[:, 2]`：选择`data` DataFrame中的第三列。
* `inputs`变量现在包含了`data` DataFrame的前两列数据。
* `outputs`变量现在包含了`data` DataFrame的第三列数据。

2. 处理缺失值：

inputs = inputs.fillna(inputs.mean())

* `.fillna(value)`：这是一个pandas DataFrame的方法，用于替换DataFrame中的缺失值（通常是`NaN`）。
* `inputs.mean()`：计算`inputs` DataFrame中每列的平均值。
* `inputs.fillna(inputs.mean())`：将`inputs` DataFrame中的缺失值替换为对应列的平均值。
* 注意：这里假设`inputs` DataFrame中的数据类型都是数值型，因为`.mean()`只能用于数值型列。如果包含非数值型列，这行代码会抛出错误。

3. 打印处理后的数据：

print(inputs)

* 这行代码会打印出经过缺失值处理后的`inputs` DataFrame。

总结：这段代码从data DataFrame中选择了前两列作为输入数据，第三列作为输出数据，并将输入数据中的缺失值替换为对应列的平均值，最后打印出处理后的输入数据。

3、课后练习实现 🔥

• 创建包含更多行和列的原始数据集。

• 删除缺失值最多的列。

• 将预处理后的数据集转换为张量格式。

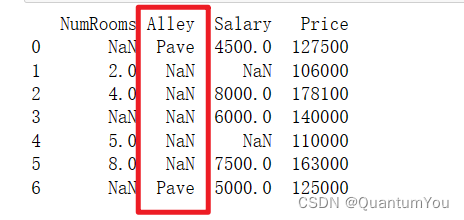
①第一步：造数据

data_test_file = os.path.join('..', 'data','house_tiny_test.csv')
with open(data_test_file, 'w') as f:
    f.write('NumRooms,Alley,Salary,Price\n') # 列名
    f.write('NA,Pave,4500,127500\n') # 每行表示一个数据样本
    f.write('2,NA,NA,106000\n')
    f.write('4,NA,8000,178100\n')
    f.write('NA,NA,6000,140000\n')
    f.write('5,NA,NA,110000\n')
    f.write('8,NA,7500,163000\n')
    f.write('NA,Pave,5000,125000\n')

data_test = pd.read_csv(data_test_file)
print(data_test)

②第二步 筛选遍历缺失值

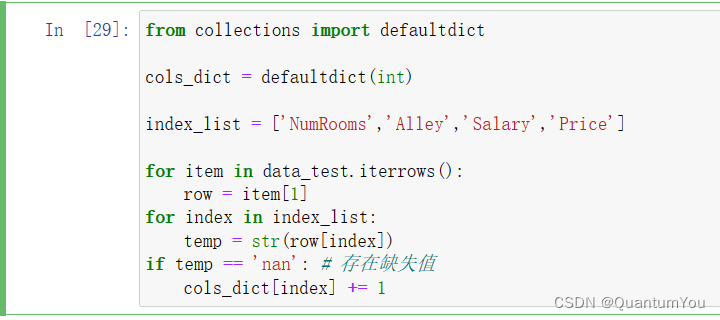
from collections import defaultdict

cols_dict = defaultdict(int)

index_list = ['NumRooms','Alley','Salary','Price']

for item in data_test.iterrows():
    row = item[1]
for index in index_list:
    temp = str(row[index])
if temp == 'nan': # 存在缺失值
    cols_dict[index] += 1

③第三步 统计降序排序

cols_dict = dict(sorted(cols_dict.items(), key=lambda x : x[1], reverse=True))

print(cols_dict.items())

④第四步 删除缺失值最多的列

data_test = data_test.drop(‘Alley’,axis=1)
data_test

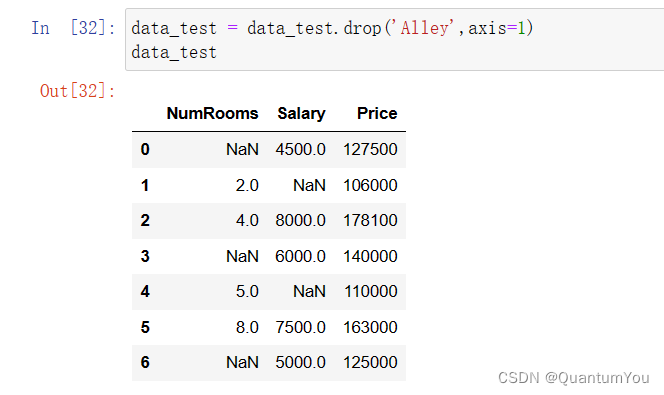
⑤第五步 处理缺失值

input_data, output_data = data_test.iloc[:, 0:2], data_test.iloc[:, 2]
input_data = input_data.fillna(input_data.mean())
print(input_data)

⑥第六步 转换为张量格式

X, y = torch.tensor(input_data.values), torch.tensor(output_data.values)
X, y

五、线性代数

在机器学习中，范数（Norm）通常用于衡量向量或矩阵的大小，或者作为正则化项来防止过拟合。

1、向量范数

1. L1 范数（L1 Norm）

   $$||\mathbf{x}|{|}_1=\sum _{i=1}^n|x_i|$$

   其中，$\mathbf{x}=[x_1,x_2,\dots ,x_n]$ 是一个向量，$n$ 是向量的维数。

2. L2 范数（L2 Norm 或欧几里得范数）

   $$||\mathbf{x}|{|}_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

   同样地，$\mathbf{x}=[x_1,x_2,\dots ,x_n]$ 是一个向量。

3. Lp 范数

   $$||\mathbf{x}|{|}_p={\left(\sum _{i=1}^n|x_i{|}^p\right)}^{\frac{1}{p}}$$

   其中 $p\ge 1$ 是一个实数。

4. L∞ 范数（最大范数）

   $$||\mathbf{x}|{|}_{\infty }=\underset{i=1}{\overset{n}{\max }}|x_i|$$

   这是向量元素中绝对值的最大值。

2、 矩阵范数

对于矩阵 $A\in {\mathbb{R}}^{m\times n}$，以下是几种常见的矩阵范数：

1. Frobenius 范数（F-范数）

   $$||A|{|}_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}^2}$$

   其中 $a_{ij}$ 是矩阵 $A$ 的元素。

2. 谱范数（Spectral Norm 或 2-范数）

   $$||A|{|}_2=\sqrt{{\lambda }_{\max }(A^{T}A)}$$

   其中 ${\lambda }_{\max }(A^{T}A)$ 是 $A^{T}A$（$A$ 的转置乘以 $A$）的最大特征值。

3. 1-范数（列和范数）

   $$||A|{|}_1=\underset{1\le j\le n}{\max }\sum _{i=1}^m|a_{ij}|$$

   这是矩阵所有列向量绝对值之和的最大值。

4. ∞-范数（行和范数）

   $$||A|{|}_{\infty }=\underset{1\le i\le m}{\max }\sum _{j=1}^n|a_{ij}|$$

   这是矩阵所有行向量绝对值之和的最大值。

3、张量算法的基本性质

下面是对照实例 A 矩阵

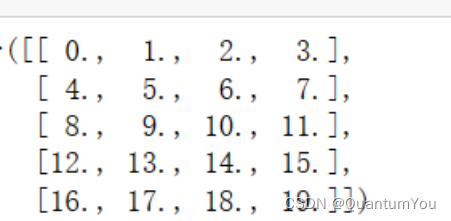
• 默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。 我们还可以[指定张量沿哪一个轴来通过求和降低维度]。 以矩阵为例，为了通过求和所有行的元素来降维（轴0），可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量，因此输入轴0的维数在输出形状中消失。
  
  指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输入轴1的维数在输出形状中消失。

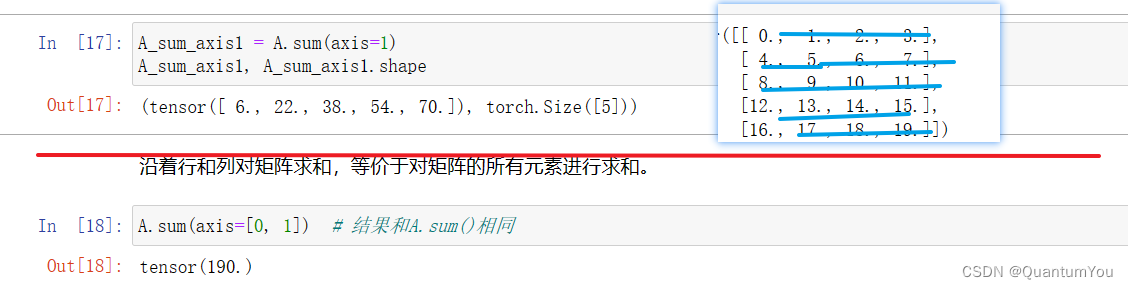
4、课后练习实现🔥

关于 E.sum(axis=2) 的解释

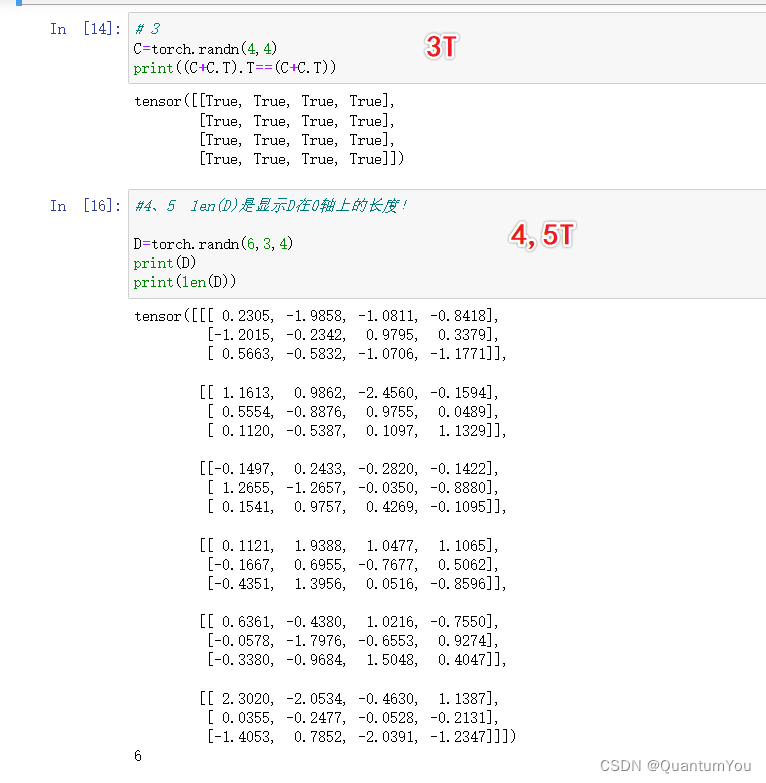
keepdims 保持形状不变

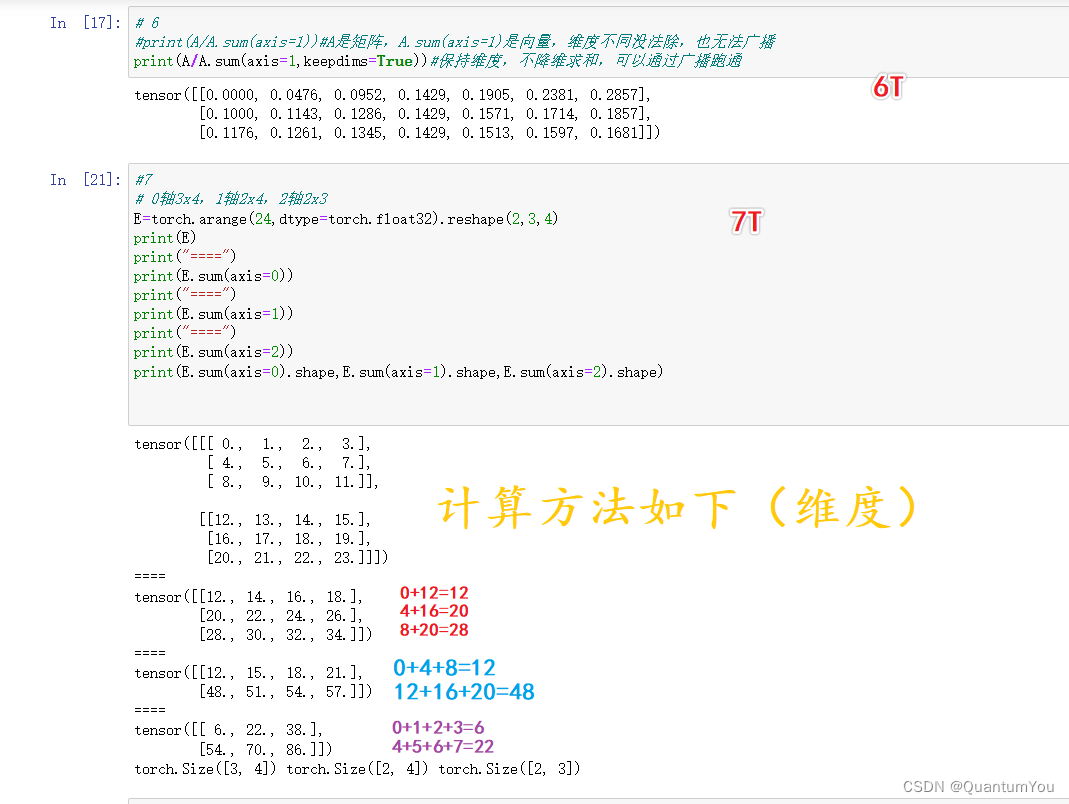
在NumPy（一个Python的数值计算库）中，E.sum(axis=2) 这样的表达式通常意味着对数组 E 沿着第三个维度（索引为2的维度）进行求和。

为了更清楚地解释，让我们考虑一个三维数组（也称为张量）的示例。

假设我们有以下三维数组 E：

import numpy as np

E = np.array([
    [[1, 2, 3], [4, 5, 6]],
    [[7, 8, 9], [10, 11, 12]]
])

这个数组的形状是 (2, 2, 3)。它有两个二维子数组（或称为“切片”），每个子数组都是 (2, 3) 的形状。

当我们执行 E.sum(axis=2) 时，我们沿着第三个维度（索引为2的维度）进行求和。这意味着对于每个二维子数组（或切片），我们都会沿着其第三个维度（实际上只有一列）进行求和。

对于上面的示例，E.sum(axis=2) 的结果将是：

array([[ 6, 15],
       [24, 33]])

这个结果数组的形状是 (2, 2)，因为我们沿着第三个维度（每个二维子数组的列）进行了求和。具体来说，6 是第一个二维子数组 [1, 2, 3] 的和，15 是 [4, 5, 6] 的和，以此类推。

1. F = torch.ones(2, 3, 4)

这个命令创建了一个形状为(2, 3, 4)的张量F，其中所有的元素都被初始化为1。这个张量有三个维度：

• 第一个维度（也称为轴0或dim=0）有2个元素。
• 第二个维度（也称为轴1或dim=1）有3个元素。
• 第三个维度（也称为轴2或dim=2）有4个元素。

因此，F可以看作是一个2x3的矩阵，其中每个元素本身又是一个长度为4的向量。

2. G = torch.ones(2, 3, 4, 5)

这个命令创建了一个形状为(2, 3, 4, 5)的张量G，其中所有的元素也被初始化为1。这个张量有四个维度：

• 第一个维度（dim=0）有2个元素。
• 第二个维度（dim=1）有3个元素。
• 第三个维度（dim=2）有4个元素。
• 第四个维度（dim=3）有5个元素。

对于F和G的Frobenius范数，它们分别是：

# 对于 F
frobenius_norm_F = torch.norm(F)
# 对于 G
frobenius_norm_G = torch.norm(G)

因此，计算torch.norm(F) * torch.norm(F)和torch.norm(G) * torch.norm(G)时，实际上是在计算这两个Frobenius范数的平方。

对于F，其Frobenius范数是：

$$\sqrt{2\times 3\times 4}=\sqrt{24}=2\sqrt{6}$$

平方后就是：

$$(2\sqrt{6}{)}^2=24$$

对于G，其Frobenius范数是：

$$\sqrt{2\times 3\times 4\times 5}=\sqrt{120}=2\sqrt{30}$$

平方后就是：

$$(2\sqrt{30}{)}^2=120$$

所以，正确的输出应该是：

tensor(24.) tensor(120.)

六、矩阵计算

梯度指向的是值变化最大的方向

关于分子布局和分母布局介绍

假设我们有一个标量函数f(y)，其中y是一个向量，我们可以将其表示为：

$$f(\mathbf{y})=f(y_1,y_2,\dots ,y_m)$$

其中$$\mathbf{y}$$是一个向量，y_1, y_2, 是该向量的元素。

1. 分子布局（Numerator Layout）：

如果我们考虑对f(y)关于y的求导，并且我们想要表示这个求导结果为分子布局，我们可以将其视为一个1×m的行向量（因为标量的维度是1×1，所以求导结果的维度与分子相同）。在LaTeX中，这个行向量可以表示为：

$$\left[\frac{\partial f}{\partial y_1},\frac{\partial f}{\partial y_2},\dots ,\frac{\partial f}{\partial y_m}\right]$$

注意，这里我们使用$$\partial$$来表示偏导数，并使用[和]来表示行向量。
2. 分母布局（Denominator Layout）：

对于分母布局，求导结果的维度与分母相同，即m×1的列向量。在LaTeX中，这个列向量可以表示为：

$$\left[\begin{array}{c}\frac{\partial f}{\partial y_1}\\ \frac{\partial f}{\partial y_2}\\ ⋮\\ \frac{\partial f}{\partial y_m}\end{array}\right]$$

注意加粗符号

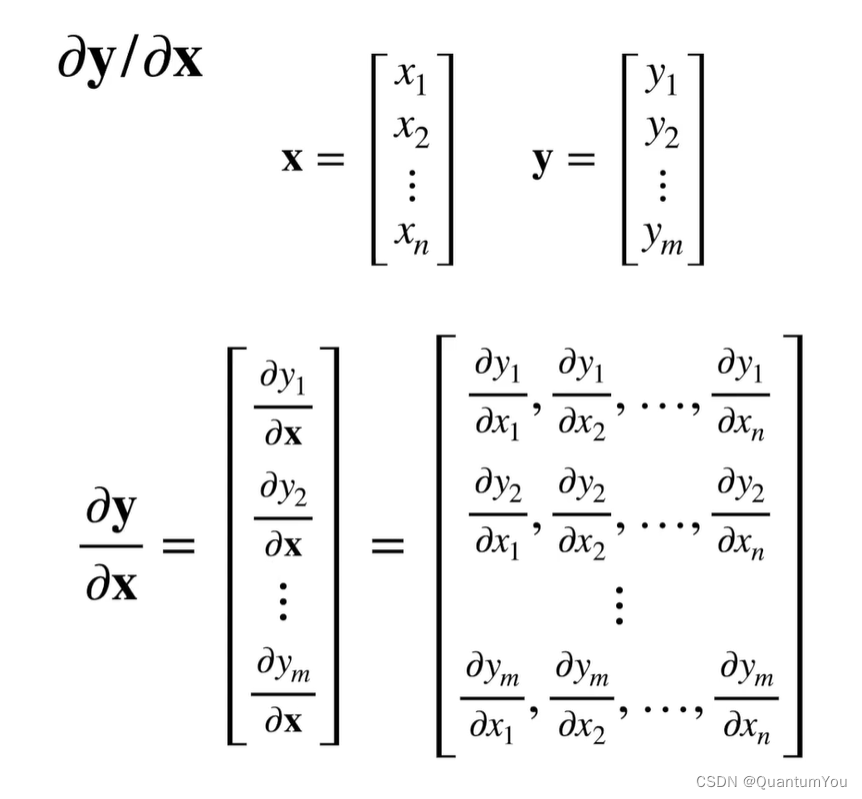
七、自动求导

• <x,w>:向量内积，x1w1+x2w2+…+xnwm=标量
• xw内积就是x转置乘以w，对w求导x转置拿出来就行

关于链式求导的举例

正向从自变量x开始算起，反向是从因变量y(或者z)开始算起

下划线代表重写内容

• SUM函数其实就是x_1+x_2+…x_n，求偏导自然是全1

1、分离计算的介绍

• 有时，我们希望[将某些计算移动到记录的计算图之外]。 例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。 想象一下，我们想计算z关于x的梯度，但由于某种原因，希望将y视为一个常数， 并且只考虑到x在y被计算后发挥的作用。

• 这里可以分离y来返回一个新变量u，该变量与y具有相同的值， 但丢弃计算图中如何计算y的任何信息。 换句话说，梯度不会向后流经u到x。 因此，下面的反向传播函数计算z=ux关于x的偏导数，同时将u作为常数处理， 而不是z=xx关于2x的偏导数。

• detach:拆卸 脱离
  

2、控制流的梯度计算

• 使用自动微分的一个好处是： [即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度]。 在下面的代码中，while循环的迭代次数和if语句的结果都取决于输入a的值。

norm()是求欧几里得范数，欧几里得范数指得就是通常意义上的距离范数。

• f(a)是a的分段线性函数，则d=f(a)=ka，梯度就是k，k=d/a
• 调用f(a)函数返回的值，是一个关于a的线性函数，所以d关于a的导数就是这个线性函数中a的系数

3、课后练习实现🔥

①绘制函数图像及其切线

%matplotlib inline
import numpy as np
from d2l import torch as d2l #在之前的代码中，已经把绘图的plot函数集成进d2l了

#1 求切线步骤：求f'(1)，f(1),切线是y-f(1)=f'(1)(x-1),即y=4x-4

x=np.arange(0.1,3,0.1)#生成一组数，起点x=0.1，终点x=3，步长是0.1
def f2(x):
    return x**3-x**(-1)
d2l.plot(x,[f2(x),4*x-4],'x','f(x)',legend=['f2(x)','df2(x)'])#plot(自变量，[函数1，函数2]……)

②反向传播连续性问题

2、在运行反向传播函数之后，立即再次运行它，看看会发生什么。

#2 会报错，默认不允许连续backward，默认需要更新x.grad才可以再backward
x=torch.randn((6),requires_grad=True)
y=2*torch.dot(x,x)
y.backward()
#y.backward(retain_graph=True)
print(x.grad)
#y.backward() #除非在第一次backward时y.backward(retain_graph=True)，否则不可以连续backward

默认不允许连续backward，默认需要更新x.grad才可以再backward

③控制流梯度随机分析

• 在控制流的例子中，我们计算d关于a的导数，如果将变量a更改为随机向量或矩阵，会发生什么？
• 重新设计一个求控制流梯度的例子，运行并分析结果。

def f(a):
    b=a*a
    for i in range(5):
        b=b+i
    if b.norm()>=0:
        d=b+10
    return d

a1=torch.randn(10,requires_grad=True)
b1=f(a1)
b1.sum().backward(retain_graph=True)#retain_graph=True，经测试控制流连续反向传播会报错，清除梯度也没用！！
print(b1)
print("====")
print(a1.grad)

#b1.backward()#若a是向量，b也是向量，没法直接用反向传播
b1.backward(torch.ones_like(a1))#对非标量调用`backward`需要传入一个`gradient`参数，该参数指定微分函数关于`self`的梯度
print(a1.grad)

 

与控制流的梯度计算进行对比

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c


a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a

八、线性回归

1、损失函数

• 在我们开始考虑如何用模型拟合（fit）数据之前，我们需要确定一个拟合程度的度量。 损失函数（loss function）能够量化目标的实际值与预测值之间的差距。 通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。 回归问题中最常用的损失函数是平方误差函数。 当样本的预测值为y^ ⁽ⁱ⁾，其相应的真实标签为y ⁽ⁱ⁾ 时， 平方误差可以定义为以下公式：

$${\ell }^{(i)}(w_1,w_2,b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2$$

$$\ell (w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n{\ell }^{(i)}(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right)}^2$$

$$w_1^{\ast },w_2^{\ast },b^{\ast }=\underset{w_1,w_2,b}{\mathrm{argmin}}\ell (w_1,w_2,b)$$

• 关于线性回归，求最优解的时候，一般没有显示解，是NP-complete问题

NP完全问题（NP-complete problem）是计算复杂度理论中决定性问题的等级之一，是NP（非决定性多项式时间）中最难的决定性问题。NP完全问题是指一类计算问题，它们具有一个重要的性质，即可以在多项式时间内验证问题的一个可能解，但要找到问题的解通常需要指数时间。

具体来说，NP完全问题具有以下几个特点：

1. 属于NP问题：这意味着它们可以在多项式时间内验证一个给定的解是否正确。
2. 难以解决：尽管可以在多项式时间内验证解的正确性，但找到问题的解通常需要指数时间，这意味着在实际中可能非常难以解决。
3. 可归约性：通过归约一个NP完全问题可以把其他NP问题转化为它。这意味着如果有一个解决NP完全问题的多项式时间算法，那么就可以解决所有的NP问题。

NP完全问题的一个著名例子是旅行商问题（Traveling Salesman Problem, TSP），即给定一系列城市和每对城市之间的距离，找到一条访问每个城市一次并返回原点的最短路径。这个问题可以在多项式时间内验证一个给定的路径是否是最短的，但要找到这样的路径通常需要指数时间。

2、基础优化算法

在训练本节讨论的线性回归模型的过程中，模型的每个参数将作如下迭代：
$$\begin{array}{rl}{w}_1& \leftarrow w_1-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial {\ell }^{(i)}(w_1,w_2,b)}{\partial w_1}=w_1-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{x}_1^{(i)}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right),\\ w_2& \leftarrow w_2-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial {\ell }^{(i)}(w_1,w_2,b)}{\partial w_2}=w_2-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{x}_2^{(i)}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right),\\ b& \leftarrow b-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial {\ell }^{(i)}(w_1,w_2,b)}{\partial b}=b-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\left(x_1^{(i)}{w}_1+x_2^{(i)}{w}_2+b-y^{(i)}\right).\end{array}$$

在上式中，$|\mathcal{B}|$ 代表每个小批量中的样本个数（批量大小，batch size），$\eta$ 称作学习率（learning rate）并取正数。需要强调的是，这里的批量大小和学习率的值是人为设定的，并不是通过模型训练学出的，因此叫作超参数（hyperparameter）。我们通常所说的“调参”指的正是调节超参数，例如通过反复试错来找到超参数合适的值。在少数情况下，超参数也可以通过模型训练学出。本书对此类情况不做讨论。

等高图拓展 -->

在机器学习中，等高图（Contour Plot）是一种可视化工具，主要用于展示多维数据的形状和变化。特别是在监督学习中的回归算法中，等高图常用于展示损失函数（如均方误差、交叉熵等）在不同参数组合下的值，从而帮助理解和优化模型。

等高图的基本原理是，在二维平面上，通过绘制一系列等值线（即等高线）来表示函数值相等的点集。这些等高线通常使用不同的颜色或线型进行区分，以便更清晰地展示函数值的变化趋势。

在机器学习中，等高图通常用于以下几个方面：

1. 梯度下降的可视化：通过绘制损失函数关于不同参数组合的等高图，可以直观地看到梯度下降算法在优化过程中的行为。例如，等高图的疏密程度可以反映函数值的变化快慢，从而判断算法的收敛速度和效果。
2. 参数选择：通过观察等高图，可以选择合适的参数组合，使得模型的性能达到最优。例如，在支持向量机（SVM）中，可以通过等高图来选择合适的惩罚参数C和核函数参数gamma。
3. 模型诊断：等高图还可以用于诊断模型的过拟合和欠拟合问题。通过观察等高图的形状和分布，可以判断模型是否对训练数据过度敏感或过于平滑，从而调整模型的复杂度或采用其他策略来改进性能。

梯度本身是上升的，而我们因为往最优解方向走，就需要负梯度方向

3、小批量随机梯度下降

选择批量大小时

• 不能太小
  每次计算量太小，不适合并行来最大利用计算资源

• 不能太大
  内存消耗增加，浪费计算，例如如果所有样本都是相同的

梯度下降通过不断沿着反梯度方向更新参数求解
小批量随机梯度下降是深度学习默认的求解算法
两个重要的超参数是批量大小和学习率

4、线性回归的实现 🔥

• 注意，1是标准差（standard deviation）

在PyTorch中，torch.normal 函数用于生成符合正态（高斯）分布的随机数。给定的代码片段 X = torch.normal(0, 1, (num_examples, len(w))) 是用来生成一个具有特定形状和参数的正态分布随机张量（tensor）。

让我们分解这个代码片段：

1. 参数：

   • 0：这是正态分布的均值（mean 或 μ）。
   • 1：这是正态分布的标准差（std 或 σ）。
   • (num_examples, len(w))：这是一个元组，指定了生成张量的形状。具体来说，num_examples 表示张量的第一个维度（通常代表样本的数量），而 len(w) 表示张量的第二个维度（可能代表每个样本的特征数量或权重的数量，这里 w 似乎是一个列表或类似的可迭代对象）。

2. 结果：

   • X：这是一个形状为 (num_examples, len(w)) 的张量，其中的元素是从均值为 0、标准差为 1 的正态分布中随机抽取的。

这个张量 X 通常用于表示一组随机样本的数据，其中每个样本都是一个 len(w) 维的向量。在机器学习和深度学习的上下文中，这样的数据通常用于训练模型或测试模型的性能。

1、生成数据集

例如，假设我们正在训练一个线性回归模型，并且我们有一组权重 w 和偏置项 b（这些可能已经在某个地方定义过了）。X 就可以作为输入数据（特征），我们可以使用模型 y_pred = X @ w + b（其中 @ 表示矩阵乘法）来预测输出 y_pred，并与真实的目标值 y 进行比较以计算损失并进行反向传播来更新权重 w 和偏置项 b。

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    #   随机参数
    X = torch.normal(0, 1, (num_examples, len(w)))
    
    y = torch.matmul(X, w) + b
    
    #  添加噪音   
    y += torch.normal(0, 0.01, y.shape)
    
    #   注意，这里使用reshape((-1, 1))将y的形状从(num_examples,)更改为(num_examples, 1) 
    return X, y.reshape((-1, 1))

注意，这里使用reshape((-1, 1))将y的形状从(num_examples,)更改为(num_examples, 1)，以确保其形状与某些机器学习库（如PyTorch）中的期望输入相匹配。

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

上面代码是定义了真实的权重true_w和偏置true_b

根据函数的输入输出可知 即为 X,Y 之间的关系。

yield就是 return 返回一个值，并且记住这个返回的位置，下次迭代就从这个位置后开始。

2、读取数据集

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

这个data_iter函数是一个数据迭代器，它用于从给定的特征和标签中随机抽取小批量（batch）数据。

1. 参数:

   • batch_size: 每个小批量中样本的数量。
   • features: 形状为[num_examples, ...]的张量，其中num_examples是样本的数量，后面的维度可以是任意的，取决于你的数据。
   • labels: 形状为[num_examples, ...]的张量，其中通常...为1（即每个样本一个标签）。

2. 初始化:

   • num_examples = len(features): 获取样本的总数。
   • indices = list(range(num_examples)): 创建一个包含所有样本索引的列表。
     随机索引
   • random.shuffle(indices): 随机打乱索引列表，这样每次迭代时样本的顺序都会不同。注意这里应该使用random.shuffle来自random模块，但为了使代码完整，可能需要添加import random。

3. 迭代过程:

   • 使用range(0, num_examples, batch_size)来生成一个范围，这个范围从0开始，到num_examples结束（但不包括num_examples），步长为batch_size。这样可以确保我们按批次遍历所有样本。
   • 对于每一个范围内的i，我们计算i: min(i + batch_size, num_examples)，这是一个切片操作，用于从indices列表中获取当前批次的索引。注意这里要防止索引超出范围。
   • 使用torch.tensor将这些索引转换为PyTorch张量，然后使用这些索引从features和labels中选择数据。
   • 使用yield关键字返回当前批次的数据。这允许函数在每次迭代时“暂停”并返回数据，而不是一次性返回所有数据。这使得迭代器在处理大量数据时更加内存友好。

这个函数的一个常见用法是在训练循环中，每次迭代时调用data_iter来获取一个小批量的数据和标签，然后用于计算梯度、更新模型参数等。

调用函数

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

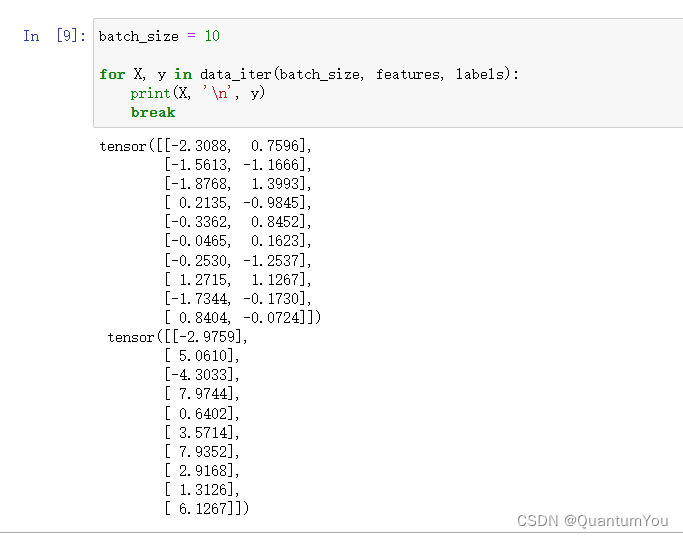
在PyTorch中，定义了两个张量w和b，通常用作线性回归或其他线性模型的权重和偏置项。下面是给出的代码段的详细解释：

3、初始化模型参数

1. 定义权重w:

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)

这行代码使用torch.normal函数来从均值为0、标准差为0.01的正态分布中抽取一个(2,1)形状的张量，即w是一个列向量，包含两个元素。

• 0：这是正态分布的均值。
• 0.01：这是正态分布的标准差。
• size=(2,1)：指定了张量的形状。这里我们想要一个2x1的张量。
• requires_grad=True：这表示PyTorch需要计算这个张量相对于某个标量值的梯度。在训练模型时，这允许我们使用自动微分来更新权重。

2. 定义偏置b:

b = torch.zeros(1, requires_grad=True)

这行代码使用torch.zeros函数来创建一个形状为(1,)（也就是一个单独的元素）的张量，并初始化为0。b通常用于表示线性模型中的偏置项。

• 1：指定了张量的形状，这里是一个单独的元素。
• requires_grad=True：同样，这表示PyTorch需要计算这个张量相对于某个标量值的梯度。

在定义了w和b之后，可能会使用它们来定义一个线性模型，例如y_pred = torch.matmul(X, w) + b，其中X是输入数据。然后，可以使用损失函数（如均方误差）来计算预测值y_pred与真实值y之间的差异，并使用优化器（如SGD、Adam等）来更新w和b的值，以最小化这个差异。

4、定义损失函数 优化算法

均方损失（Mean Squared Error, MSE）的公式可以写作：

$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

但是，在的squared_loss函数中，并没有明确地除以样本数量n（这通常在计算整个数据集的均方损失时才会做），而是直接计算了每个样本的损失，并且损失是除以2的（尽管除以2在优化过程中不影响最优解，但通常MSE不会除以2）。因此，函数是直接计算每个样本的损失，并且损失是除以2的，那么可以写作：

$${\text{Loss}}_i=\frac{1}{2}(y_i-{\hat{y}}_i{)}^2$$

这里i表示第i个样本，y_i是真实值，\hat{y}_i是预测值。注意这个公式只适用于单个样本的损失计算，而不是整个数据集的MSE。

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

优化算法

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

lr — learning_rate学习率

5、训练模型

定义超参数

lr = 0.03
num_epochs = 3   #  扫三次
net = linreg
loss = squared_loss

模板

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

这段代码中的每个部分都有其特定的目的，解释每一部分：

1. 外层循环：

   for epoch in range(num_epochs):
   

   这是训练循环的外层循环，用于控制训练的轮数（epoch）。num_epochs定义了整个数据集将被遍历多少次。

2. 内层循环：

   for X, y in data_iter(batch_size, features, labels):
   

   内层循环使用data_iter迭代器来按批次获取数据和标签。batch_size定义了每个批次中样本的数量。

3. 前向传播和损失计算：

   l = loss(net(X, w, b), y)  # X和y的小批量损失
   

   这行代码首先通过net函数（通常是一个前向传播函数）计算预测值，然后计算预测值和真实值y之间的损失。loss函数计算了均方误差或其他类型的损失。

4. 反向传播：

   l.sum().backward()
   

   由于l的形状是(batch_size, 1)，即每个样本都有一个损失值，我们需要将这些损失值加在一起（通过.sum()）得到一个标量，然后调用.backward()来计算关于模型参数[w, b]的梯度。

5. 参数更新：

   sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
   

   这行代码假设有一个名为sgd的函数，它接收模型参数列表、学习率lr和批次大小batch_size（尽管在这个例子中batch_size可能并未在sgd函数内部使用，除非是为了某种特定的学习率调整策略）。该函数使用梯度来更新参数。

6. 每个epoch结束后的评估：

   with torch.no_grad():
       train_l = loss(net(features, w, b), labels)
       print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
   

   在每个epoch结束后，代码评估整个训练集上的损失。由于不需要计算梯度（因为我们只是评估性能），所以使用torch.no_grad()上下文管理器。然后，它计算整个训练集上的损失并打印出来。注意，这里使用.mean()来获取所有样本损失的平均值，因为train_l的形状可能是(num_examples,)，其中num_examples是训练集中的样本数量。

总之，这段代码实现了一个简单的训练循环，用于通过梯度下降来优化模型的参数。在每个epoch中，它遍历训练数据的所有批次，更新参数，并在epoch结束时评估整个训练集上的性能。

九、softmax 回归

• 分类问题和回归问题是机器学习和数据分析中常见的两种问题类型，它们之间存在明显的区别。

1、分类问题(离散)

• 分类问题是监督学习中的一种重要问题。它的目标是确定数据点所属的分类或类别。在分类问题中，输入数据（特征）被用来预测一个离散的输出变量（类别）。例如，根据电子邮件的内容和特征，将其分类为垃圾邮件或正常邮件；根据病人的症状、生理指标和医学历史，将病人的疾病分类为不同的病种或疾病阶段；在图像识别中，将图像分类为不同的对象（如猫、狗、汽车等）。

解决分类问题的常见机器学习算法包括决策树、朴素贝叶斯、逻辑回归、支持向量机（SVM）、随机森林、梯度提升机（Gradient Boosting）和神经网络（包括深度学习）等。

拓展：决策树介绍

决策树是一种监督学习算法，用于分类和回归任务。

以下是一些关于决策树的关键信息：

1. 基本概念：决策树通过一系列规则对数据进行分割，形成树状结构，每个分支代表一个决策结果，最终达到叶节点时得到分类结果。
2. 构建过程：决策树的构建从根节点开始，选取最优划分属性，递归地将数据集分为子集，直到满足停止条件。停止条件通常是节点上的样本属于同一类别或没有更多特征可供划分。
3. 关键指标：在构建过程中，需要计算信息增益、增益率、信息熵等指标来选择最佳划分属性。这些指标帮助确定如何分割数据以获得最有效的决策路径。
4. 优点：决策树易于理解和解释，可以处理数值型和类别型数据，不需要任何数据准备工作。同时，它能够处理多输出问题并且适合处理缺失值。
5. 缺点：容易产生过拟合，对于非线性问题可能需要更复杂的树结构。对于包含大量数值型特征的数据集，可能会不稳定。
6. 应用场景：决策树广泛用于医学诊断、金融风险评估、营销响应预测等领域。
7. 工具使用：可以使用sklearn库中的DecisionTreeClassifier类来构建决策树模型，并通过训练数据来拟合模型，进而对新数据进行预测。

2、回归问题(连续)

• 回归问题也是监督学习的一种问题。与分类问题不同，回归问题的目标是预测一个连续的输出变量（例如价格、数量、分数等）。在回归问题中，输入数据（特征）被用来预测一个连续的输出值。例如，根据历史房屋销售数据预测下个月房价；根据销售产品的历史数据预测当月销售额；根据用户的行为数据预测其可能的收入；根据用户的个人信息和交易记录来预测其信用级别。

• 解决回归问题的常见机器学习算法包括线性回归、多项式回归、岭回归（Ridge Regression）、套索回归（Lasso Regression）、弹性网络（ElasticNet Regression）、决策树回归、随机森林回归、梯度提升回归（Gradient Boosting Regression）和神经网络（包括深度学习）等。

拓展： 独热编码

独热编码（One-Hot Encoding），也称为一位有效编码或独热编码表示，是用来表示离散变量（categorical data）的一种方法。在机器学习和深度学习中，经常会使用独热编码来将离散变量转换为多维向量，以便于算法处理。

独热编码的原理是将离散型的特征数据映射到一个高维空间中，每个可能的取值都对应于高维空间的一个点，在这些点上取值为1，其余均为0。例如，假设我们有一组汽车品牌数据，包含三种品牌：Benz、BMW、Audi。使用独热编码对这组数据进行编码后，可以得到以下结果：

• Benz：1 0 0
• BMW：0 1 0
• Audi：0 0 1

可以看到，原本三种汽车品牌的离散数据被编码为了一组由3个元素组成的向量，每个元素的取值要么是0，要么是1。

独热编码的优点包括：

1. 解决分类数据处理问题：独热编码将离散分类特征转换为机器学习算法易于处理的二进制格式，提高了算法对离散特征的处理能力。
2. 避免引入数值偏误：通过将每个类别映射到独立的二进制向量，独热编码消除了类别间可能存在的错误数值关系，从而避免了算法基于这些关系做出不准确的预测。

然而，独热编码也存在一些缺点，如资源消耗量大，因为对于具有n个不同取值的特征，独热编码会将其转换为一个长度为n的二进制向量。

• Oy和Qi都是概率，p(y)和p(i)的意思

softmax回归是一个多类分类模型
使用Softmax操作子得到每个类的预测置信度
使用交叉熵来来衡衡量预测和标号的区别

softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布：

$${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=\text{softmax}(o_1,o_2,o_3)$$

其中

$${\hat{y}}_1=\frac{\exp (o_1)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_2=\frac{\exp (o_2)}{{\sum }_{i=1}^3\exp (o_i)},{\hat{y}}_3=\frac{\exp (o_3)}{{\sum }_{i=1}^3\exp (o_i)}.$$

容易看出${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$且$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1$，因此${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3$是一个合法的概率分布。这时候，如果${\hat{y}}_2=0.8$，不管${\hat{y}}_1$和${\hat{y}}_3$的值是多少，我们都知道图像类别为猫的概率是80%。此外，我们注意到

$$\underset{i}{\mathrm{argmax}}{o}_i=\underset{i}{\mathrm{argmax}}{\hat{y}}_i$$

因此softmax运算不改变预测类别输出。

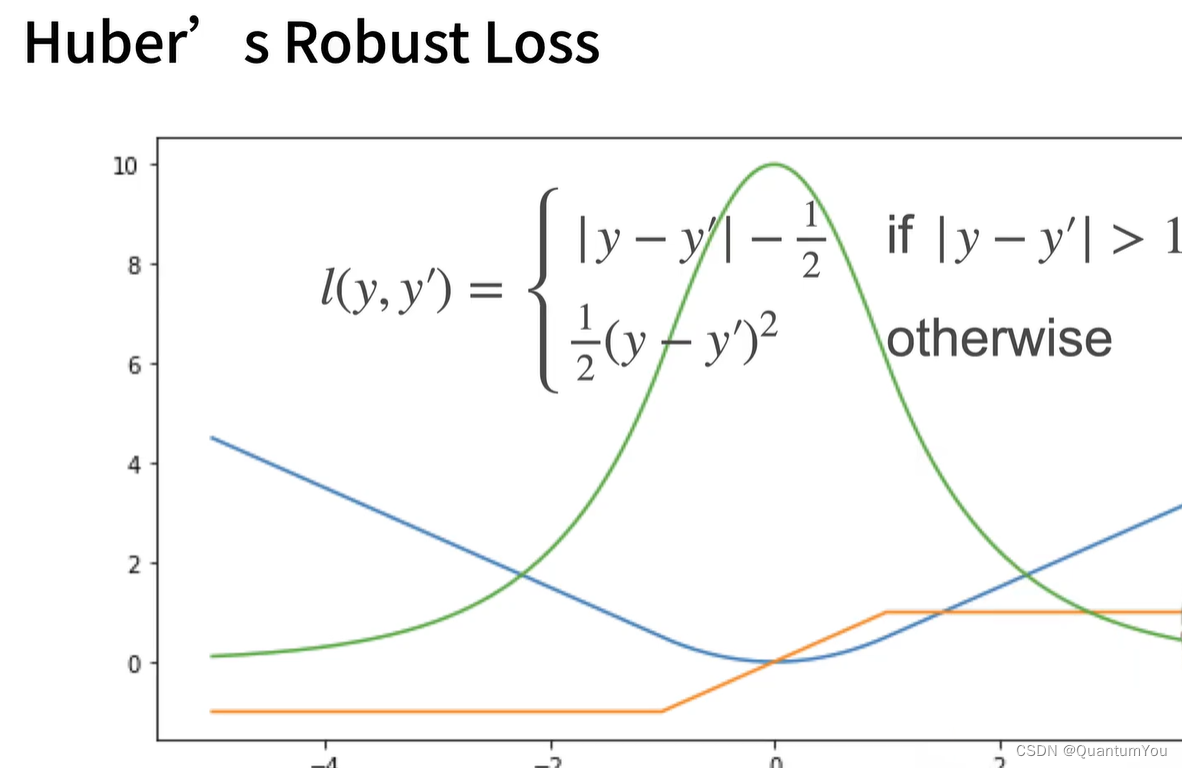
蓝色是 y=0 时，变化 y^/ 的情况,绿色为其似然函数（高斯分布即正态分布），橙色为其损失函数梯度

拓展：似然函数

似然函数是表示带有参数的数学模型表达时，在已知模型的结果时，对于参数的可能性、即此参数的概率

似然函数（Likelihood Function）是统计学和机器学习中一个非常重要的概念，尤其在参数估计和模型选择中。它描述了在给定模型参数下，观测到一组特定数据（或称为“证据”）的概率。

定义上，似然函数是给定输出$X=x$时，关于参数$\theta$的函数$L(\theta |x)$，其中$x$是观测到的数据，$\theta$是模型参数。似然函数不是概率分布，因为参数$\theta$通常不是随机变量，而是未知的固定值。然而，似然函数可以被视为参数$\theta$的“条件概率”，即在给定观测数据$x$的情况下，参数$\theta$取某个值的概率。

在参数估计中，似然函数常常用于最大似然估计（Maximum Likelihood Estimation, MLE）。最大似然估计是一种通过最大化似然函数来估计模型参数的方法。其背后的思想是：在给定观测数据的情况下，应该选择使这些数据出现概率最大的参数作为估计值。

例如，考虑一个二项分布$B(n,p)$，其中$n$是试验次数，$p$是成功概率（即模型参数）。如果我们进行了$n$次试验，并观测到$k$次成功，那么似然函数就是$L(p|k)=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}$。为了找到使似然函数最大的$p$值，我们可以对$L(p|k)$关于$p$求导并令其等于零，解出$p$的值。这个解就是$p$的最大似然估计值。

需要注意的是，似然函数和概率密度函数（或概率质量函数）在形式上可能很相似，但它们的解释和用途是不同的。概率密度函数描述的是随机变量的概率分布，而似然函数描述的是在给定观测数据下参数取值的概率。

关于上图的解释：

• 从图可以看到，在y=0的时候，当某个参数使得 y^/ 能取值为0，那么这个参数是最有可能接近样本参数的。

• 而这个“最有可能”，就是概率，就是似然函数的值，也是对应了绿色曲线的顶点

• 绿色的线似然函数代表了 y^/ 在哪儿取值时，这个 y^/ 对应的参数概率是最大的

• y固定， y^/ 变化，蓝色的线代表了 y^/ 偏离y的程度

3、简易实现图片分类 🔥

①下载数据集测试集

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=True)

②获取数据集标签

def get_fashion_mnist_labels(labels):  
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

定义了函数 get_fashion_mnist_labels，它接受一个包含Fashion-MNIST数据集标签索引的列表 ，并返回这些索引对应的文本标签列表。Fashion-MNIST 是一个包含 10 个不同时尚类别的图像数据集。

下面是该函数的详细解释：

1. 函数名：get_fashion_mnist_labels
2. 参数：labels - 一个包含Fashion-MNIST标签索引的列表或可迭代对象。这些索引通常是从 0 到 9 的整数，对应着 10 个不同的时尚类别。
3. 函数体内部定义了一个列表 text_labels，它包含了 Fashion-MNIST 数据集中每个类别的文本标签。这些文本标签按照与标签索引相同的顺序排列。
4. 函数使用列表推导式（list comprehension）遍历 labels 中的每个索引 i，并通过 int(i) 将其转换为整数（尽管在大多数情况下，传入的 i 已经是整数，但这样做可以确保兼容性）。然后，它使用这些整数索引从 text_labels 列表中检索相应的文本标签。
5. 最后，函数返回包含所有文本标签的列表。

③绘制图像

  def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

定义了一个名为 show_images 的函数，用于在 Matplotlib 的图表中绘制图像列表。这个函数接受以下参数：

• imgs: 一个图像列表，可以是 PyTorch 张量（tensors）或 PIL 图像。
• num_rows: 绘制图像的行数。
• num_cols: 绘制图像的列数。
• titles: 可选参数，一个标题列表，与图像列表相对应。
• scale: 缩放因子，用于调整图表的大小。

以下是该函数的工作流程：

1. 计算图表大小：根据 num_rows、num_cols 和 scale 计算图表的大小。

2. 创建子图：使用 d2l.plt.subplots 创建一个子图网格，并返回一个包含所有子图的 NumPy 数组。

3. 扁平化子图数组：使用 flatten 方法将子图数组转换为一维数组，以便在循环中迭代。

4. 绘制图像：对于每个子图和对应的图像，执行以下操作：

   • 检查图像是否是 PyTorch 张量。如果是，则使用 .numpy() 方法将其转换为 NumPy 数组。
   • 使用 imshow 方法在子图上绘制图像。
   • 隐藏子图的 x 轴和 y 轴。
   • 如果提供了标题列表，则为子图设置标题。

5. 返回子图数组：函数最后返回包含所有子图的数组。

6. 绘图

# PIL图片
ax.imshow(img)

如果img不是PyTorch张量（由前面的if torch.is_tensor(img):检查判断），则假设它是一个PIL（Python Imaging Library，或其更现代的分支Pillow）图像。在这种情况下，直接使用ax.imshow(img)来在当前的matplotlib轴上显示这个PIL图像。

2. 隐藏

ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)

这两行代码的目的是隐藏当前轴（ax）的x轴和y轴。ax.axes实际上是ax自身的一个引用（因为在matplotlib中，轴对象通常也包含一个对自身的引用，名为axes），所以可以直接使用ax来代替ax.axes。但是，为了保持与原始代码的一致性，这里使用了ax.axes。

• get_xaxis()和get_yaxis()方法分别返回当前轴的x轴和y轴对象。
• set_visible(False)方法将这些轴设置为不可见。

3. 设置标题

if titles:
    ax.set_title(titles[i])

如果调用show_images函数时提供了titles参数（并且它不是一个空列表或None），则这段代码会为当前轴（ax）设置标题。标题的内容是titles列表中与当前图像索引i相对应的元素。

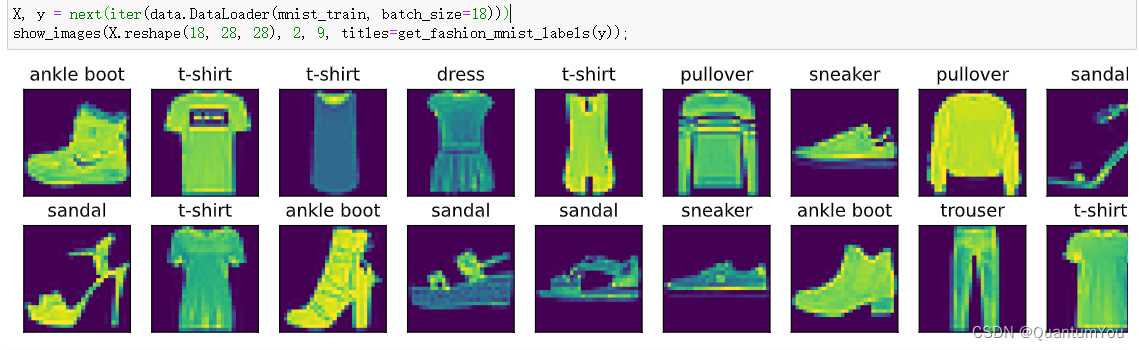
④读取小批量数据

• 注意读取数据的速度要跟上数据训练的速度

1. 定义get_dataloader_workers函数:

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

这是一个简单的函数，它返回4。这是为了设置DataLoader的num_workers参数，该参数指定了用于数据加载的子进程数量。在这个例子中，我们使用4个子进程来并行地读取和加载数据。这可以提高数据加载的效率，尤其是在大规模数据集和/或多核CPU的情况下。

2. 创建train_iter数据加载器:

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
                             num_workers=get_dataloader_workers())

这里，使用了PyTorch的DataLoader类来创建一个名为train_iter的数据加载器。这个加载器将用于在训练过程中迭代地加载MNIST训练集的数据。

• mnist_train：这应该是一个PyTorch的Dataset对象，它包含了MNIST训练集的数据。
• batch_size：如前面所述，每次迭代时加载的样本数量。
• shuffle=True：在每个epoch开始时，打乱数据集中的样本顺序。这有助于模型更好地泛化，因为它会在不同的迭代中看到不同的样本组合。
• num_workers=get_dataloader_workers()：使用前面定义的get_dataloader_workers函数来确定用于数据加载的子进程数量。在这个例子中，我们使用了4个子进程。

⑤整合组件并测试

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

4、softmax 回归简易实现 🔥

• 在深度学习和其他机器学习任务中，数据通常是以批处理（batches）的形式进行处理的，而不是一次性处理整个数据集。这有几个原因：

1. 内存限制：对于大型数据集，将整个数据集加载到内存中可能是不现实的。通过分批处理，可以仅加载一部分数据到内存中，从而允许处理大型数据集。
2. 随机梯度下降（SGD）：在训练神经网络时，我们经常使用随机梯度下降（或其变种，如Adam、RMSProp等）来优化模型参数。SGD依赖于小批量的随机数据来估计梯度，而不是整个数据集的梯度。
3. 并行计算：许多深度学习框架（如TensorFlow、PyTorch等）都支持GPU加速。通过小批量处理，可以更容易地利用GPU的并行计算能力。

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

这里，batch_size 被设置为256，意味着在训练和测试时，数据将被分成大小为256的批次进行处理。

• d2l.load_data_fashion_mnist(batch_size) 是一个函数调用，它加载了Fashion-MNIST数据集，并返回两个迭代器（iterators）：train_iter 和 test_iter。
• train_iter 用于迭代训练集中的批次数据。
• test_iter 用于迭代测试集中的批次数据。

Fashion-MNIST是一个包含70,000个时尚服饰产品图像的数据集，分为10个类别。这些图像是28x28像素的灰度图像。

① 初始化参数

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

定义线性层（或称为全连接层）的参数。具体来说，这里定义了一个权重矩阵 W 和一个偏置向量 b，这些参数通常用于神经网络中的线性变换。

1. 定义输入和输出维度:

   • num_inputs = 784: 这通常对应于一个28x28的图像（像素数量），因为 28x28 = 784。在Fashion-MNIST或MNIST这样的数据集中，图像的尺寸就是28x28。
   • num_outputs = 10: 这意味着网络将预测10个不同类别的概率（对于Fashion-MNIST或MNIST，这10个类别是不同的服饰或数字）。

2. 定义权重矩阵 W:

   • torch.normal(0, 0.01, size=(num_inputs, num_outputs)): 这会生成一个形状为 (num_inputs, num_outputs) 的矩阵，其中的元素是从均值为0、标准差为0.01的正态分布中随机抽取的。这通常是为了在训练开始时为权重赋予随机的、小的初始值，以帮助网络进行学习。
   • requires_grad=True: 这表示PyTorch需要计算这个张量（在这个例子中是权重矩阵）的梯度。在反向传播时，这些梯度将被用于更新权重。

3. 定义偏置向量 b:

   • torch.zeros(num_outputs): 这会生成一个长度为 num_outputs 的全零向量。这是偏置项，它在每个输出节点上添加一个可学习的偏移量。
   • 同样，requires_grad=True 表示PyTorch需要计算这个偏置向量的梯度。

按行和列压缩

$$softmax(X{)}_{i}j=\frac{\exp (X_{i}j)}{{\sum }_k\exp (X_{i}k)},$$

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

• 在PyTorch中，torch.normal 用于生成正态（高斯）分布的随机数，而 softmax 函数通常用于将模型的输出转换为概率分布（在分类任务中）

② 进行softmax

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

-1 是二维度但是不指定维数

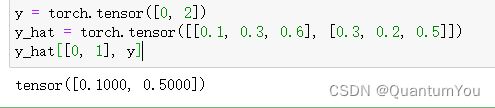
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

• 不使用Python的for循环迭代预测（这往往是低效的）， 而是通过一个运算符选择所有元素。 下面，我们[创建一个数据样本y_hat，其中包含2个样本在3个类别的预测概率， 以及它们对应的标签y。] 有了y，我们知道在第一个样本中，第一类是正确的预测； 而在第二个样本中，第三类是正确的预测。 然后(使用y作为y_hat中概率的索引)， 我们选择第一个样本中第一个类的概率和第二个样本中第三个类的概率。
  

https://www.zhihu.com/question/23765351/answer/2144591565

即y_hat[[0,1],[0,2]],取第0行和第1行,第0列和第2列

y = torch.tensor([0, 2])的意思是第一个样本的真实类别为0，第二个样本的真实类别为2

• 这样的话 y_hat[[0, 1], y] 表示的是预测为正确类别的概率 !!!

③定义损失函数

• range(len(y_hat))，其实可以写成y_hat.shape[0]，提取y_hat矩阵的行数

这句话的意思就是锁定y轴在x轴上根据labels抽取预测值

对于单个样本，如果y是类别的索引（例如，y = c表示第c个类别），那么交叉熵损失为：

$$L=-\log (p_c)$$

其中，p_c是模型预测第c个类别的概率。

然而，在实际应用中，我们通常会处理一个批量的样本。假设我们有一个批量的真实标签y（每个样本一个标签）和一个批量的预测概率p（每个样本一个概率分布向量），则平均交叉熵损失为：

$$L=-\frac{1}{N}\sum _{i=1}^N\log (p_{i,y_i})$$

其中，N是批量中的样本数，p_{i, y_i}是第i个样本预测为真实类别y_i的概率。

④ 预测准确度

计算预测结果 y_hat 和真实标签 y 之间的准确率。

1. 检查维度：
   函数首先检查 y_hat 的维度是否大于1且第二维度（即类别数）是否大于1。这是为了确定 y_hat 是否为概率分布矩阵（每行代表一个样本的概率分布）。如果是这样，则使用 argmax 函数找出每个样本最可能的类别（即概率最大的类别）。

2. 类型转换：
   在比较 y_hat 和 y 之前，函数将 y_hat 的数据类型转换为 y 的数据类型。这是为了确保两者类型一致，从而可以进行比较。然而，在 cmp = y_hat.type(y.dtype) == y 之后，又将 cmp 的类型再次转换为 y.dtype，

3. 返回准确率：
   函数返回 cmp 中 True 的数量作为准确率，但是它是将 cmp 的和转换为 y.dtype 类型的浮点数。这可能会导致类型不匹配的问题，特别是当 y.dtype 不是浮点数类型时。而且，由于 cmp 的和已经是整数了（表示预测正确的数量），我们只需要将其转换为浮点数并除以总数即可得到准确率。

class Accumulator:   
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]



def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

这个函数 evaluate_accuracy 的目的是计算一个模型在给定的数据集上的准确率。它使用了一个名为 Accumulator 的辅助类

1. 函数定义：

   • net: 传入要评估的模型，通常是一个 torch.nn.Module 的实例。
   • data_iter: 传入一个数据迭代器，它应该生成批量数据 (X, y)，其中 X 是输入数据，y 是对应的标签。

2. 设置模型为评估模式：

   • net.eval()：这行代码将模型设置为评估模式。在评估模式下，模型的某些层（如 Dropout 和 BatchNorm）会改变其行为，以在评估时给出更准确的预测。

3. 初始化累加器：

   • metric = Accumulator(2)：创建一个累加器对象，用于存储两个值：正确预测的数量和总的预测数量。我们假设 Accumulator 类有一个 add 方法，用于添加这两个值。

4. 关闭梯度计算：

   • with torch.no_grad():：这个上下文管理器确保在评估过程中不会计算梯度，从而节省内存和计算资源。

5. 遍历数据集：

   • 对于数据迭代器中的每一批数据 (X, y)，函数都会：
     • 使用模型 net 对输入数据 X 进行预测，得到预测结果 y_hat。
     • 计算这一批数据的准确率 accuracy(net(X), y)。这里假设 accuracy 函数接受预测结果和真实标签作为输入，并返回这一批数据中正确预测的数量。
     • 使用 metric.add 方法将这一批数据的正确预测数量和总预测数量添加到累加器中。

6. 返回准确率：

   • 函数最后返回的是累加器中的正确预测数量除以总预测数量，即整个数据集的准确率。

⑤开始训练

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期 """
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

class Animator:  
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型 """
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

这个 train_ch3 函数是用于训练一个神经网络模型的。它包含了训练循环、测试准确率的计算和动画的更新。

参数

• net: 要训练的神经网络模型。
• train_iter: 训练数据集的数据迭代器。
• test_iter: 测试数据集的数据迭代器。
• loss: 损失函数，用于计算模型预测和真实标签之间的损失。
• num_epochs: 训练的总轮数（epoch）。
• updater: 更新器，用于更新模型的参数，通常是优化器和参数的组合。

函数体

1. 初始化动画器：
   使用 Animator 类 来创建一个动画器对象。这个动画器将用于绘制训练损失、训练准确率和测试准确率随训练轮数的变化。

2. 训练循环：
   对于每一个训练轮数（epoch），执行以下操作：

   • 调用 train_epoch_ch3 函数 来训练模型，并返回训练损失和训练准确率。
   • 调用 evaluate_accuracy 函数来计算模型在测试集上的准确率。
   • 使用动画器的 add 方法来更新动画，将当前轮数、训练损失、训练准确率和测试准确率作为参数传入。

3. 断言检查：
   在训练完成后，函数执行三个断言（assert）语句来检查训练结果是否满足一些预定义的条件。这些条件包括：

   • 训练损失应该小于 0.5。
   • 训练准确率应该在 0.7 和 1 之间。
   • 测试准确率也应该在 0.7 和 1 之间。

   如果任何一个断言失败，程序将抛出一个 AssertionError 异常，并显示不满足条件的值。

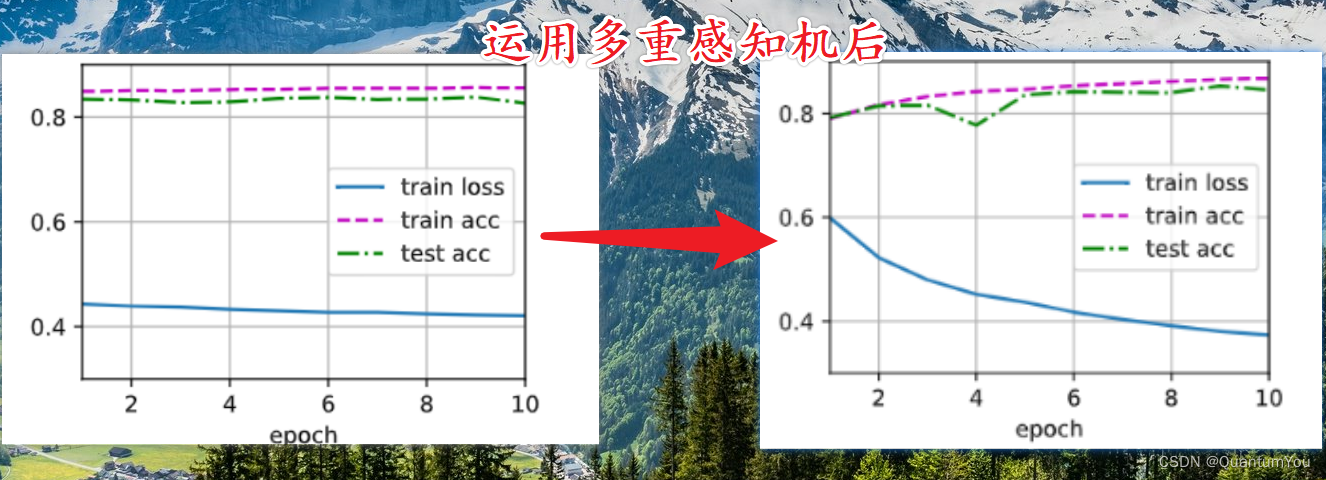
感觉训练的损失效果有点差😢,太平缓了😭

⑥预测结果

预测结果还是准确的，毕竟acc 0.85以上

十、感知机学习

• 感知机（Perceptron）是最简单的单层人工神经网络，也是二元线性分类模型，是神经网络和支持向量机的基础。感知机学习旨在求出将训练数据集进行线性划分的分类超平面，为此，导入了基于误分类的损失函数，然后利用梯度下降法对损失函数进行极小化，从而求出感知机模型。

感知机是集语音、文字、手语、人脸、表情、唇读、头势、体势等多通道为一体的，并对这些通道的信息进行编码、压缩、集成、融合的计算机智能接口系统。现阶段的研究重点包括大词汇量实时中国手语的识别、PC版和掌上电脑版中国手语合成系统、人脸图像的监测与识别等。

感知机的工作原理可以概括为以下步骤：

1. 初始化：对权重和偏置进行随机初始化。
2. 前向传播：将输入数据通过激活函数，得到输出值。
3. 计算损失：将输出值与真实标签进行比较，计算损失。
4. 反向传播：根据损失调整权重和偏置。
5. 迭代：重复步骤2-4，直到达到预设的迭代次数或损失达到预设的最小值。

1、训练感知机

具体来说，给定一个小批量样本$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，其批量大小为$n$，输入个数为$d$。假设多层感知机只有一个隐藏层，其中隐藏单元个数为$h$。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为$\mathbf{H}$，有$\mathbf{H}\in {\mathbb{R}}^{n\times h}$。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为${\mathbf{W}}_h\in {\mathbb{R}}^{d\times h}$和 ${\mathbf{b}}_h\in {\mathbb{R}}^{1\times h}$，输出层的权重和偏差参数分别为${\mathbf{W}}_o\in {\mathbb{R}}^{h\times q}$和${\mathbf{b}}_o\in {\mathbb{R}}^{1\times q}$。

我们先来看一种含单隐藏层的多层感知机的设计。其输出$\mathbf{O}\in {\mathbb{R}}^{n\times q}$的计算为

$$\begin{array}{rl}\mathbf{H}& =\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h,\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}_o+{\mathbf{b}}_o,\end{array}$$

也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到

$$\mathbf{O}=(\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h){\mathbf{W}}_o+{\mathbf{b}}_o=\mathbf{X}{\mathbf{W}}_h{\mathbf{W}}_o+{\mathbf{b}}_h{\mathbf{W}}_o+{\mathbf{b}}_o.$$

从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为${\mathbf{W}}_h{\mathbf{W}}_o$，偏差参数为${\mathbf{b}}_h{\mathbf{W}}_o+{\mathbf{b}}_o$。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

dl/dw=d(-y*<w,x>)/dw=-y*(xdw/dw+wdx/dw)=-y*x因为dw/dw=1,dx/dw=0

2、收敛定理

SVM唯一，感知机不唯一

感知机不能拟合XOR函数，它只能产生线性分割面

总结：
感知机是一个二分类模型，是最早的A模型之一
它的求解算法等价于使用批量大小为1的梯度下降
它不能拟合XOR函数，导致的第一次A!寒冬

3、多层感知机

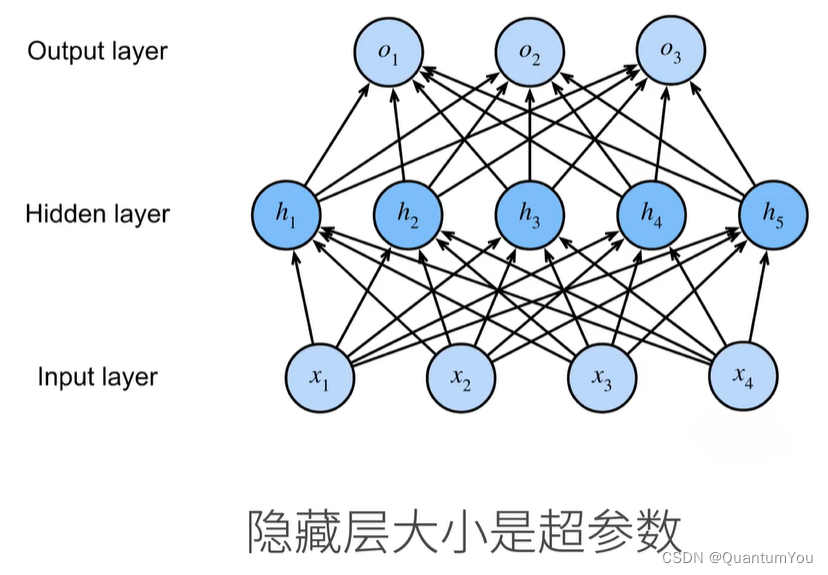
不搞激活函数，效果等价于线性回归
不加激活函数的化，构造的还是单层感知机
激活函数防止层数塌陷

超参数：隐藏层数，每层隐藏层的大小

4、代码实现 🔥

 num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

1. 定义网络参数：

   • num_inputs = 784：输入层有784个神经元，这对应于一个28x28的图像，因为28x28=784。
   • num_outputs = 10：输出层有10个神经元，这通常用于10分类问题，如手写数字识别（0-9）。
   • num_hiddens = 256：隐藏层有256个神经元。

2. 初始化权重矩阵：

   • W1：从标准正态分布（均值为0，标准差为1）中随机生成一个num_inputs x num_hiddens的矩阵，并将其乘以0.01来缩小权重的初始范围。这样做有助于模型在训练开始时更加稳定。
   • W2：类似地，从标准正态分布中随机生成一个num_hiddens x num_outputs的矩阵，并同样乘以0.01。

3. 初始化偏置向量：

   • b1：一个长度为num_hiddens的零向量。
   • b2：一个长度为num_outputs的零向量。

4. 将参数定义为PyTorch的Parameter：

在PyTorch中，nn.Parameter是一个张量，但它被自动注册为模型参数，因此当调用.parameters()或.named_parameters()方法时，它们会被包括在内。此外，当使用优化器（如torch.optim.SGD）时，这些参数也会被包括在内以进行梯度下降。

神经网络模型定义

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

开始训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

训练过程变化图

• 这次训练的很成功，各项指标都很好😄😃🌹
• 损失结果最终低于0.4
  
  
  
  
• 预测的结果也是没问题

• 这次主要运用多层感知机解决了softmax回归实现的损失度变化平缓问题