MATLAB 实现路由算法详细教程（完整代码+数据）

news2024/11/17 5:50:26

问题描述：

鉴于我们小组成员都来自计通学院，我们对专业知识计算机网络内的路由器进行研究。我们知道在整个互联网中，有着很多个小的无法互相连通的小网络，早在上世纪六十年代，针对不同网络无法互联的问题，路由器诞生了。路由器就是连通不同网络的中间媒介，在整个网络里又有无数个路由器相互连接通往不同的网络，使得网络内的主机能够相互通信，才有了今天的网络互连的时代。不难理解，在网络中，一台路由器传送信息到另一台路由器，为了节省开销和延时，必然要选择最短路径。在路由器中存在着路由表，记录着每个路由器与其下一跳路由器的距离（所有可达距离中的最短距离）。在计算机网络中，最常见的路由选择协议 OSPF 便解决了这个问题。接下来，我们将用数学实验所学知识，利用 MATLAB 实现路由器转发功能（OSPF 协议的最短路径优先）的实现，即路由算法。

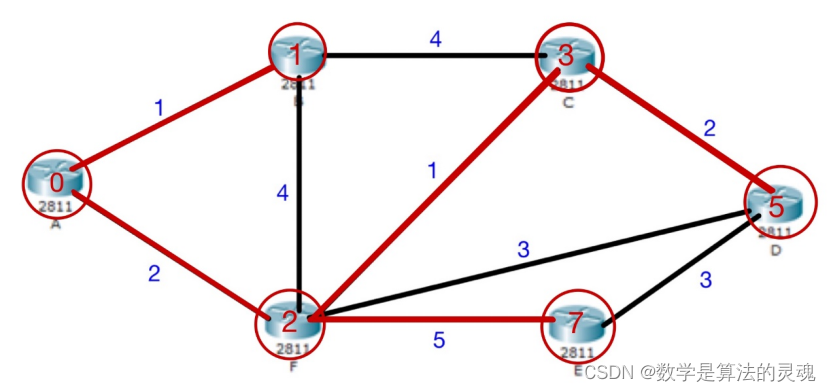
假设在某一网络中，存在着六台路由器，我们给这些路由器编号 A,B，C，D，E，F。他们的在网络里的链路关系如下图所示：

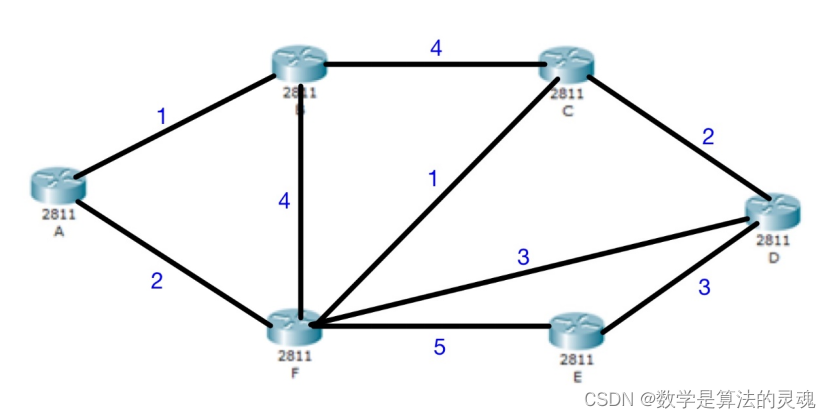
问题分析与模型建立：

根据图论的相关知识，对于给定的任意一点，存在着多条链路到底其他的各个点；我们在这里利用路由算法的分析寻找最短路径的线路计入指定点的一张表中，在路由器又称路由表。

首先，先定义几个变量：

结点个数 n；

二维矩阵 M（nxn），距离矩阵，连通的结点间即为距离，不连通的结点间为正无穷，和自己的距离为 0；

一维矩阵 pb（1xn），若第 i 点已找到最短路径，则 fp（i）=1，否则等于 0，对于初始结点，fp=1；

距离矩阵 d（1xn），若第 i 点已找到最短路径，则的 d（i）=最短距离，否则为 0，初始结点 d=0；

上一结点矩阵 path（1xn)，若第 i 点找到了最短路径，则 path 存放这一条最短路径的前一个结点，通过对每一点的回溯，可以找到最短路径。

根据距离写出以下距离矩阵，这个矩阵一定是对称矩阵，因为 A 到 B 距离与 B 到 A 距离一定是一样的。

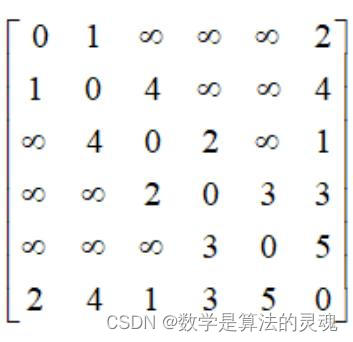
我们拿路由器 A 举例分析：对于 A 自身，则 pb(1)=1

在图中，结点上，我们将已找到最短路径的点标为它的最短距离，（可以理解为 A 路由器已找到最短路径，距离为 0），未找到的其余点表为正无穷（即表示不连通）。

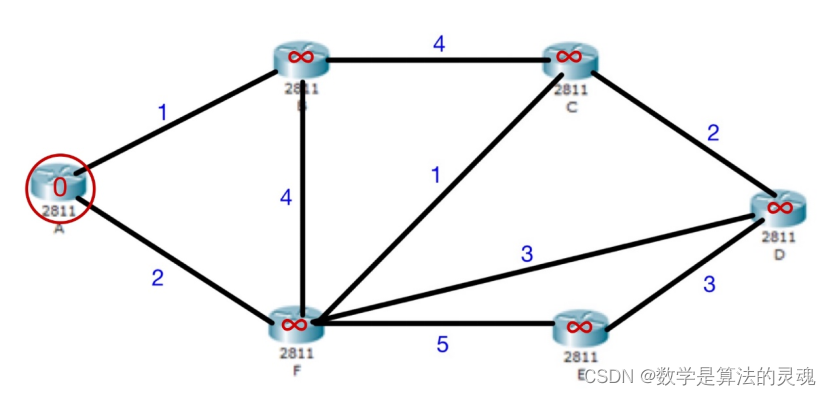
在与 A 连通的点中，即在矩阵 m 的第 1 行，寻找最小值，最小值所在列即确定的最短路径的结点，如同 B 最短，pb（2）=1，d（2）=1，对于已找到最短路径的 B 上一结点为 A，path（2）=1；

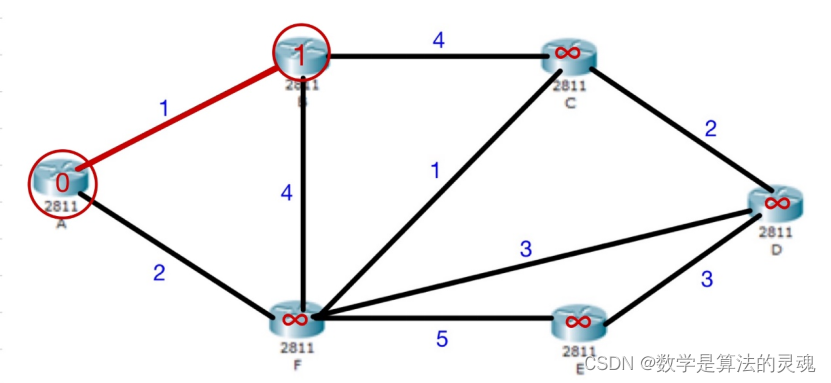
接着，在

a) 与 A 连通的，且未找到最短距离的节点的距离

b) 与 B 连通的，且未找到最短距离节点的距离 +B 的最短距离

以上两种中寻找最短距离，最短为 F，pb（6）=1；d（6）=2； path（6)=1;

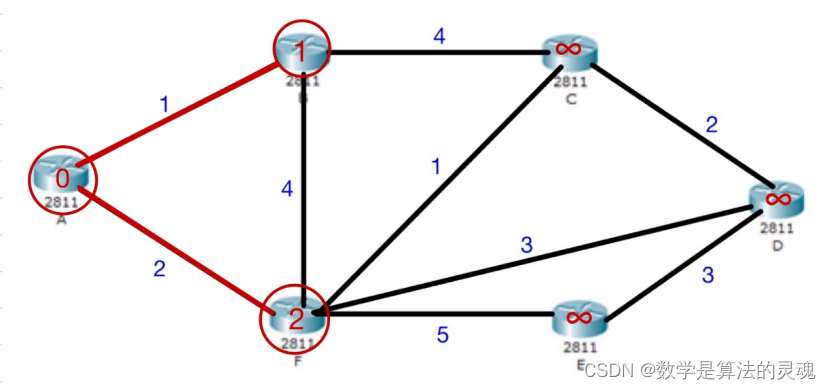
重复以上步骤，在

a) 与 A 连通的，且未找到最短距离的节点的距离

b) 与 B 连通的，且未找到最短距离节点的距离 +B 的最短距离

c) 与 F 连通的，且未找到最短距离节点的距离 +F 的最短距离

以上三种中寻找最短路径，最短为 C,pb(3)=1;d(3)=3);path(3)=6;

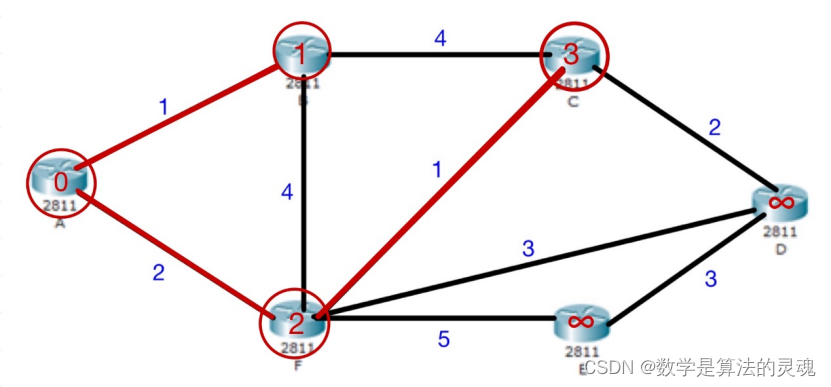
我们可以发现，所要寻找的最短路径即为

a) 对于已找到最短路径的点（包括初始结点），在与其连通的，未找到最短路径的结点中，将之间距离与圆圈中的距离（即上一结点已找到的最短路径）相加，求得的最小值。

b) 如果有多个相同的最短距离，任取其中一个。

c) 最终最短路径即距离如下图:

问题解决：

根据模型的基本成型后：我们开始利用 MATLAB 对路由表 A 的相关信息，即路由器 A 到达其他路由器的最短路径距离。

通过过程分析代码解决主要包括三个部分：

距离矩阵的建立：

n=6;   %设置距离矩阵的大小
temp=1;  %设置起始点
m=zeros(6);%定义6阶零矩阵
m(1,2)=1;m(1,6)=2;%定义矩阵中相连存在实际距离的点
m(2,1)=1;m(2,3)=4;m(2,6)=4;
m(3,2)=4;m(3,4)=2;m(3,6)=1;
m(4,3)=2;m(4,5)=3;m(4,6)=3;
m(5,4)=3;m(5,6)=5;
m(6,1)=2;m(6,2)=4;m(6,3)=1;m(6,4)=3;m(6,5)=5;
for i=1:n	%将不互通的点间距离置为无穷大
    for j=1:n
       if(m(i,j)==0)
           m(i,j)=inf;
       end
    end
end
for i=1:n	%将自己和自己相连的距离置为零
    m(i,i)=0;
end

最短路径算法的实现：

pb(1:length(m))=0;
pb(temp)=1;%求出最短路径的点为1，未求出的为0
d(1:length(m))=0;%存放各点的最短距离
path(1:length(m))=0;%存放各点最短路径的上一点标号
while sum(pb)<n %判断每一点是否都已找到最短路径
 	  tb=find(pb==0);%找到还未找到最短路径的点
fb=find(pb);%找出已找到最短路径的点
 	  min=inf;
 	  for i=1:length(fb)
     	  for j=1:length(tb)
         	  plus=d(fb(i))+m(fb(i),tb(j));  %比较已确定的点与其相邻未确定点的距离
         	  if((d(fb(i))+m(fb(i),tb(j)))<min)
               min=d(fb(i))+m(fb(i),tb(j));
               lastpoint=fb(i);
               newpoint=tb(j);
         	  end
     	  end
 	  end
 	  d(newpoint)=min;
pb(newpoint)=1;
 	  path(newpoint)=lastpoint; %最小值时的与之连接点
end

展示运行结果：

d		%展示A路由器到其他各个路由器

全部代码：

n=6;   %设置距离矩阵的大小
temp=1;  %设置起始点
m=zeros(6);%定义6阶零矩阵
m(1,2)=1;m(1,6)=2;%定义矩阵中相连存在实际距离的点
m(2,1)=1;m(2,3)=4;m(2,6)=4;
m(3,2)=4;m(3,4)=2;m(3,6)=1;
m(4,3)=2;m(4,5)=3;m(4,6)=3;
m(5,4)=3;m(5,6)=5;
m(6,1)=2;m(6,2)=4;m(6,3)=1;m(6,4)=3;m(6,5)=5;
for i=1:n	%将不互通的点间距离置为无穷大
    for j=1:n
       if(m(i,j)==0)
           m(i,j)=inf;
       end
    end
end
for i=1:n	%将自己和自己相连的距离置为零
    m(i,i)=0;
end
pb(1:length(m))=0;
pb(temp)=1;%求出最短路径的点为1，未求出的为0
d(1:length(m))=0;%存放各点的最短距离
path(1:length(m))=0;%存放各点最短路径的上一点标号
while sum(pb)<n %判断每一点是否都已找到最短路径
 	  tb=find(pb==0);%找到还未找到最短路径的点
fb=find(pb);%找出已找到最短路径的点
 	  min=inf;
 	  for i=1:length(fb)
     	  for j=1:length(tb)
         	  plus=d(fb(i))+m(fb(i),tb(j));  %比较已确定的点与其相邻未确定点的距离
         	  if((d(fb(i))+m(fb(i),tb(j)))<min)
               min=d(fb(i))+m(fb(i),tb(j));
               lastpoint=fb(i);
               newpoint=tb(j);
         	  end
     	  end
 	  end
 	  d(newpoint)=min;
pb(newpoint)=1;
 	  path(newpoint)=lastpoint; %最小值时的与之连接点
end
d		%展示A路由器到其他各个路由器