什么是背包问题
背包问题是有N件物品,容量为V的背包
每个物品有两个属性:体积,价值,分别用数组v,w表示
第i件物品的体积为v[i],价值为w[i]
计算在背包装得下的情况下,能装的最大价值是多少?
根据不同的限制条件,主要有以下三种背包问题:
- 01背包
- 完全背包
- 多重背包
01背包
每件物品最多用一次
朴素做法
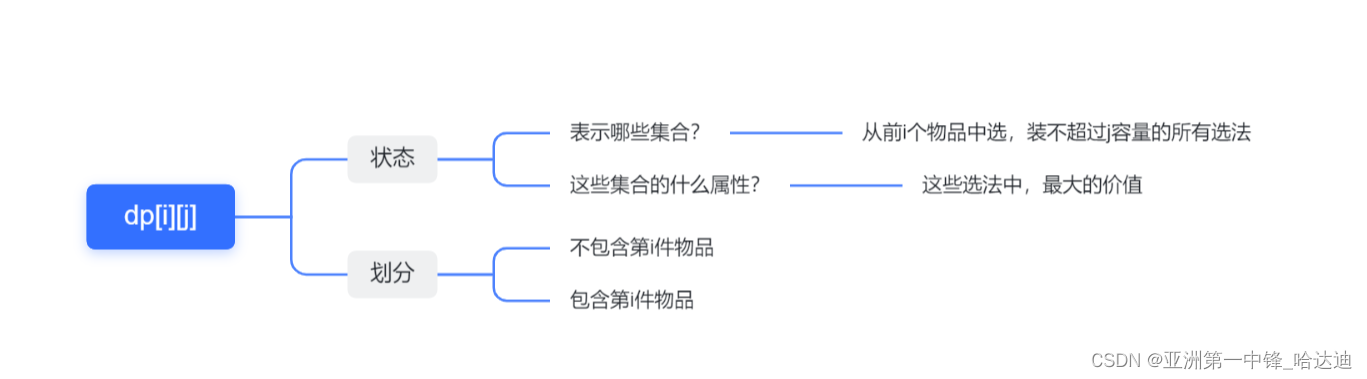
定义二维数组dp,dp[i][j]表示
- 哪些集合:从前i个物品中选,装不超过j容量的所有选法
- 什么属性:这些选法中,最大的价值
根据dp数组的定义,dp[N][V]就是最终要求解的答案
接下来看一个普遍的位置dp[i][j],其表示的集合可以划分为哪些集合?
所有从前i个物品中选,装不超过j容量的所有选法中,可以被不重不漏地划分为:
- 不包含第i件物品
- 包含第i件物品
dp[i][j] = max(前i件物品中选且不包含第i件物品的最大价值,前i件物品中选且包含第i件物品的最大价值)
前i件物品中选且不包含第i件物品的最大价值,和dp[i - 1][j]的定义是一样的
前i件物品中选且包含第i件物品的最大价值,这种情况可以将所有的选法中第i件物品的价值提出来,除了第i件物品的价值外,还要加上在前i-1件物品中选,容量不超过j - v[i]的最大价值,这和dp[i - 1][j - v[i]]的定义一样
因此dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])
我们只要在计算dp[i][j]时,保证其依赖的项已经计算过,计算过程就是正确的,
怎么保证之前的已经计算过呢?按照如下的循环方式计算:
public static int bag01 ( int N, int V, int [] w, int []v) {
int [][] dp = new int [N+ 1 ][V+ 1 ];
for ( int i = 1 ;i <= N;i++) {
for ( int j = 0 ;j <= V;j++) {
dp[i][j] = dp[i- 1 ][j];
if (j >= v[i]) {
dp[i][j] = Math. max (dp[i][j], dp[i- 1 ][j-v[i]] + w[i]);
}
}
}
return dp[N][V];
}
空间优化
可以发现在计算第i层时,只用到了第i-1层,这样可以用一个只有两层的数组滚动计算
进一步,可以发现使用到的j,要么是第i-1层的j,要么是第i-1层j的左侧,不是j左右两侧都依赖,因此可以优化为只使用一层的数组
需要注意在计算每一层的数据时,不能从左往右计算,因为会将本层的数据覆盖掉本该是上一层的数据
需要从右往左计算:
public static int bag01(int N,int V,int[] w,int []v) {
int[] dp = new int[V+1];
for (int i = 1;i<=N;i++) {
for (int j = V;j >= v[i];j--) {
dp[j] = Math.max(dp[j], dp[j-v[i]] + w[i]);
}
}
return dp[V];
}
完全背包
每件物品可以用无数多次
朴素做法
定义二维数组dp,dp[i][j]表示
- 哪些集合:从前i个物品中选,装不超过j容量的所有选法
- 什么属性:这些选法中,价值的最大的价值
所有从前i个物品中选,装不超过j容量的所有选法中,可以被不重不漏地划分为:
- 第i个物品不选
- 第i个物品选1个
- 第i个物品选2个
- …
- 第i个物品选k个(k * v[i] 需要小于等于j)
即:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + 2*w[i] ..... dp[i-1][j - k[i]] + k*w[i])
代码实现为:
public static int bagComplete(int N,int V,int[] w,int []v) {
int[][] dp = new int[N+1][V+1];
for (int i = 1;i<=N;i++) {
for (int j = 0;j <= V;j++) {
for (int k = 0;k * v[i] <= j;k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][j-k * v[i]] + k * w[i]);
}
}
}
return dp[N][V];
}
时间优化
上面的朴素做法在时间复杂度上是一个三重循环,为O(N ^ 3),可以优化为O(N ^ 2)
我们列出dp[i][j]和dp[i][j - v[i]]的公式对比:
可以发现dp[i][j]从第二项开始直到结束,和dp[i][j - v[i]]的第一项直到结束,十分相似
区别在于dp[i][j]的每一项比dp[i][j - v[i]]的每一项多了w[i]
那么dp[i][j]从第二项开始往后的最大值,等于dp[i][j - v[i]]的值加上 w[i],再结合dp[i][j]的第一项得到:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])

代码可以优化为:
public static int bagComplete(int N,int V,int[] w,int []v) {
int[][] dp = new int[N+1][V+1];
for (int i = 1;i<=N;i++) {
for (int j = 0;j <= V;j++) {
dp[i][j] = dp[i-1][j];
if (j >= v[i]) {
dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i]] + w[i]);
}
}
}
return dp[N][V];
}
空间优化
同样,完全背包也可以优化为只用一层数组:
由于使用的上一层j位置的值,和当前层j左边位置的值,因此需要在每一层从左往右遍历,这点和01背包不一样:
public static int bagComplete02(int N,int V,int[] w,int []v) {
int[] dp = new int[V+1];
for (int i = 1;i<=N;i++) {
for (int j = v[i];j <= V;j++) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
return dp[V];
}
01背包和多重背包的区别
这两个问题的最终版代码十分相似,唯一的区别就是:
- 01背包:每一层从右往左推
- 完全背包:每一层从左往右推
多重背包
每件物品能用的次数由一个数组c表示,第i件物品能用c[i]次
朴素做法
定义二维数组dp,dp[i][j]表示
- 哪些集合:从前i个物品中选,装不超过j容量的所有选法
- 什么属性:这些选法中,价值的最大的价值
所有从前i个物品中选,装不超过j容量的所有选法中,可以被不重不漏地划分为:
- 第i个物品不选
- 第i个物品选1个
- 第i个物品选2个
- …
- 第i个物品选k个(k * v[i] 需要小于等于j,且k小于等于c[i] )
代码如下:
public static int bagMulti(int N,int V,int[] w,int []v, int[] c) {
int[][] dp = new int[N+1][V+1];
for (int i = 1;i<=N;i++) {
for (int j = 0;j <= V;j++) {
for (int k = 0;k * v[i] <= j && k <= c[i]; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][j - k * v[i]] + k * w[i]);
}
}
}
return dp[N][V];
}
时间优化
朴素做法的时间复杂度为O(N^3),可否像完全背包那样优化呢?
我们列举dp[i][j]和 dp[i][j - v[i]]的每一项:

我们需要dp[i][j - v[i]]中,除了最后一项以外其他项的最大值,但无法根据整体的最大值推算局部的最大值
因此无法像完全背包那样优化
二进制优化
例如当s[i] = 19,
我们将其打包为分别有1,2,4,8,4个第i件物品的组,在这些组中用01背包的方式计算最大价值
打包规则为:另k=0,从1,2,4,8,16一直往后累加,直到s[i] - k小于k为止,将s[i] - k作为最后一组打包
例如:s[i] = 100时,打包成以下几组: 1,2,4,8,16,32,37
即在5个组中选,每个物品最多选1次
这个做法和第i件物品,最多选19次,是否等价呢?
-
dp[1][j] = max(dp[0][j], dp[0][j - v[i]] + w[i])- 表示第选0个和选1个的最大值
-
dp[2][j] = max(dp[1][j], dp[1][j - 2*v[i]] + 2*w[i])- 表示选0到1个的最大值,和选2到3的最大值,即选0到3的最大值

-
dp[3][j] = max(dp[2][j], dp[2][j - 4*v[i]] + 4*w[i])- 表示选0到3的最大值,和选4到7的最大值,即选0到7的最大值

-
依次类推,
dp[5][j] = max(dp[4][j], dp[4][j - 4*v[i]] + 4*w[i])- 表示选0到15的最大值,和选4到19的最大值,即选0到19的最大值
因此将其按照二进制打包成更小的组,在这些组上最01背包,和原始问题是等价的!
实现代码如下:
public static int bagMulti(int N,int V,int[] w,int []v, int[] c) {
// 开字够大的空间
int[] neww = new int[N * 32];
int[] newv = new int[N * 32];
int cnt = 0;
for (int i = 1;i<=N;i++) {
int k = 1;
while (k <= c[i]) {
// 将每个物品按照二进制打包成不同的组,构造成01背包问题
cnt++;
neww[cnt] = k * w[i];
newv[cnt] = k * v[i];
c[i] -= k;
k *= 2;
}
if (c[i] >= 0) {
cnt++;
neww[cnt] = k * w[i];
newv[cnt] = k * v[i];
}
}
// 按照01背包模板计算
int[] dp = new int[cnt+1];
for (int i = 1;i<=cnt;i++) {
for (int j = V;j>=newv[i];j--) {
dp[i] = Math.max(dp[i], dp[i - newv[i] + neww[i]);
}
}
return dp[cnt];
}
假设c[i]的平均值为C,这种做法的时间复杂度为O(NVlogC)



![[apidoc]Apidoc-文档生成工具](https://img-blog.csdnimg.cn/52459d24cdac447ab41005a53841695b.png)