A题 钢板最优切割路径问题
(完整资料在文末获取)

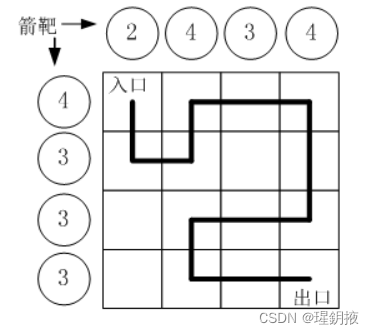
1. 建立坐标系和表示方法:
在建模之前,我们需要将切割布局转换为数学表示。首先,我们可以将布局中的每个点表示为二维坐标系中的一个点。例如,B1可以表示为坐标 (x1, y1),B2可以表示为坐标 (x2, y2),以此类推。
2. 确定切割线和边界线:
根据给定的切割布局,我们需要确定哪些线段是切割线,哪些是边界线。通常,切割线是实线部分,而边界线是布局的外边缘。这可以通过对布局进行扫描并检测实线和边缘线来实现。
3. 制定切割规则:
在启发式算法中,我们需要制定一些规则来确定切割路径。这些规则可以基于几何形状、距离、连续性等因素。例如,可以采用最近邻规则,选择与当前位置距离最近的切割线作为下一个切割点。
4. 设计算法:
基于上述建模和规则,我们可以设计一个算法来寻找最优切割路径。这个算法可以是递归的、迭代的或者其他形式的。在每一步中,算法需要根据切割规则选择下一个切割点,直到所有需要切割的线段都被切割。

5. 计算空程总长度:
在算法完成后,我们可以计算空程总长度。空程是指在切割过程中,移动到下一个切割点时没有进行实际切割的距离。因此,我们需要在算法执行过程中记录每一步的空程距离,并将它们相加得到总长度。
6. 优化和评估:
完成算法后,可以对其进行优化和评估。优化可能涉及调整切割规则、算法参数或者引入其他优化技术。评估可以通过比较算法的性能、空程长度和其他指标来进行。

示例:
作为示例,可以采用简单的最近邻规则来设计一个启发式算法:
从切割起始点开始,找到距离最近的切割线作为下一个切割点。
将当前位置移动到切割点,并记录空程距离。
重复步骤1和2,直到所有需要切割的线段都被切割。
B题 未来新城背景下的交通需求规划与可达率问题
未来新城背景下的交遢需求规划与可达率间题
在未来新城的背景下,交通需求规划和可达率问题成为了城市规划和发展的关键因素。随着城市化的快速推进和人口增长,新城的发展不仅需要满足居民的居住需求,还要考虑到交通系统的高效运作,确保居民的出行便捷和经济活动的顺畅。这篇论文将探讨未来新城中交通需求规划的策略,以及如何通过提高可达率来优化交通网络,实现社会经济的可持续发展。
整体的前提条件信息可以整理为以下内容:
1交通需求定义交通需求指定起点到终点之间的车辆流量个以起点Ⅰ到终点
4为例,总需求为100辆车。
2略径分配。路径1-2-4上分配了40辆车,而路径1-4上分配了60辆车。
这个过程称为交通需求分配。
3正常情况下的可达率计算。在没有任何阻砒的情况下,从起点Ⅰ到终点4的
交通可达率为100%,计算方法为40辆+60辆)/100辆。
4应对夹发状况的可达率变化r碁路度J-2发生交通事故导致无法通行,原本
通过1-2-4的车辆无法到达终点。此时,只有通过1-3-4的60辆车能够到达目的地,因此新的可达京为yooi00=60%.
5路径散量的假设每个起点和终点之间的路径数量假设不超过5条,且各路
段长度设为单低优先选择距离短的路径。
6车氯类型的假设。假设所有车辆均为无人驾驶车辆,且均按照系统预先规划
的路径行驶.
心交撑童值的设定。交通流量值可以为任意非负实数,不要求取整数。
问题一
图2为一个小型交通网络。各(起点,终点)对之间的交通需求见附件1。请建立数学模型,给出各(起点,终点)对之间交通需求分配到对应路径上的交通量,使得网络中任意1条路段出现突发状况时(每个路段出现突发状况概率相同)。