文章目录
- `1. AVL树的定义`
- `2. C++实现AVL树`
- 2.1 插入——左左型的右旋
- 2.2 插入——右右型的左旋
- `3. 总结`
1. AVL树的定义
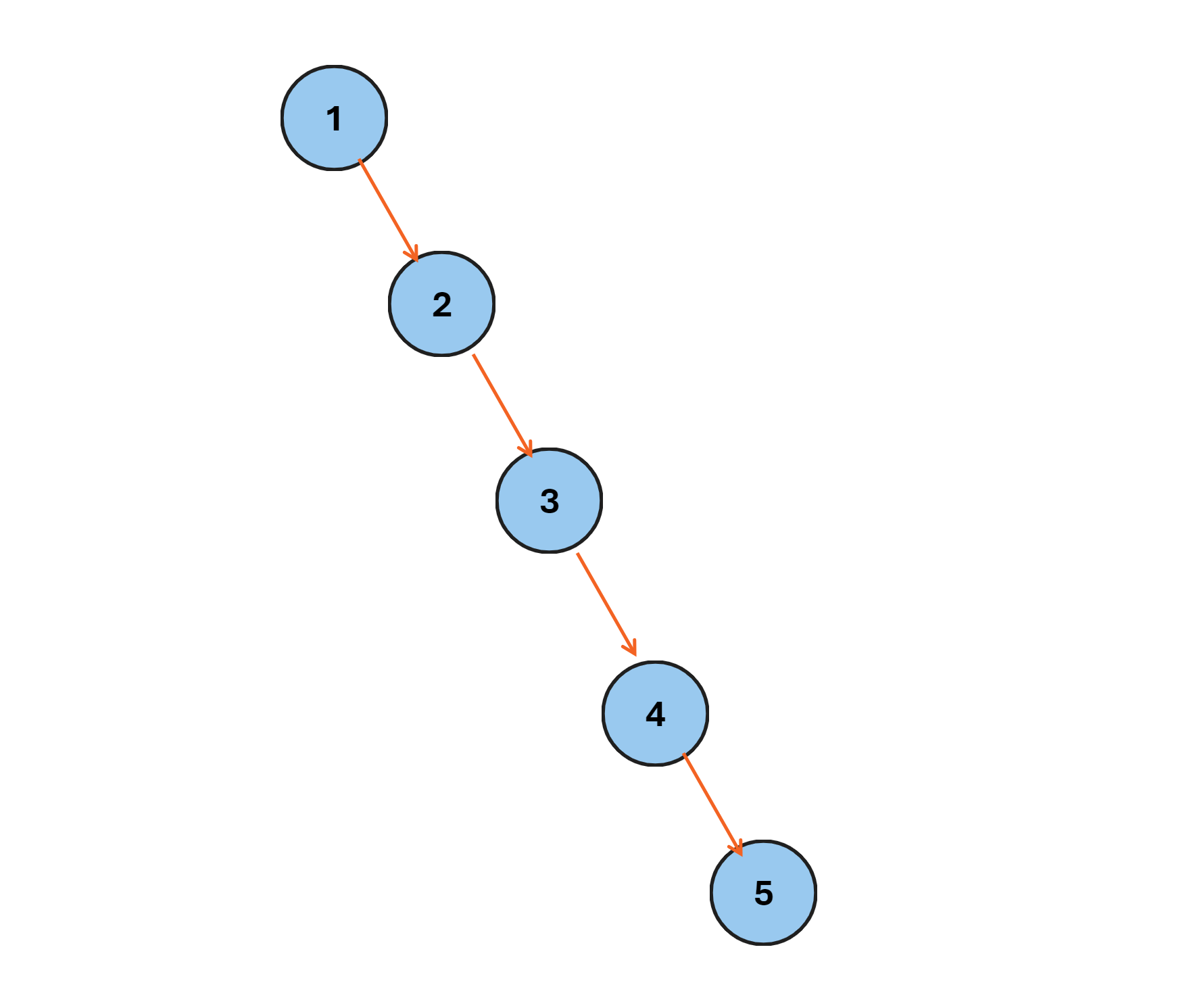
二叉搜索树(BST)是一个节点一个节点进行插入的,当插入的数据是有序的时候,二叉搜索树会退化成类似于单链表的形式,此时二叉搜索树的查询效率会无限接近O(N),类似于下图,然而我们期待的是最多查找次数为高度次,即时间复杂度是O(logN)。
AVL树是什么意思呢?
两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
因此AVL树本质上是一棵二叉搜索树,但是具有以下性质:
- 它的左右子树都是AVL树;
- 左右子树的高度之差(简称平衡因子)的绝对值不超过1 (-1,0,1)。
👨🏻💻平衡因子简介
平衡因子(bf),英文 balance factor,即左右子树高度之差。
- 平衡因子 = 右子树高度 - 左子树高度
在AVL树中,必须要保证 -1 <= bf <= 1;
👨🏻💻计算平衡因子
下图的二叉树,计算每个节点的平衡因子,图示如下:(左图为左右子树的高度的分析,右图为平衡因子)
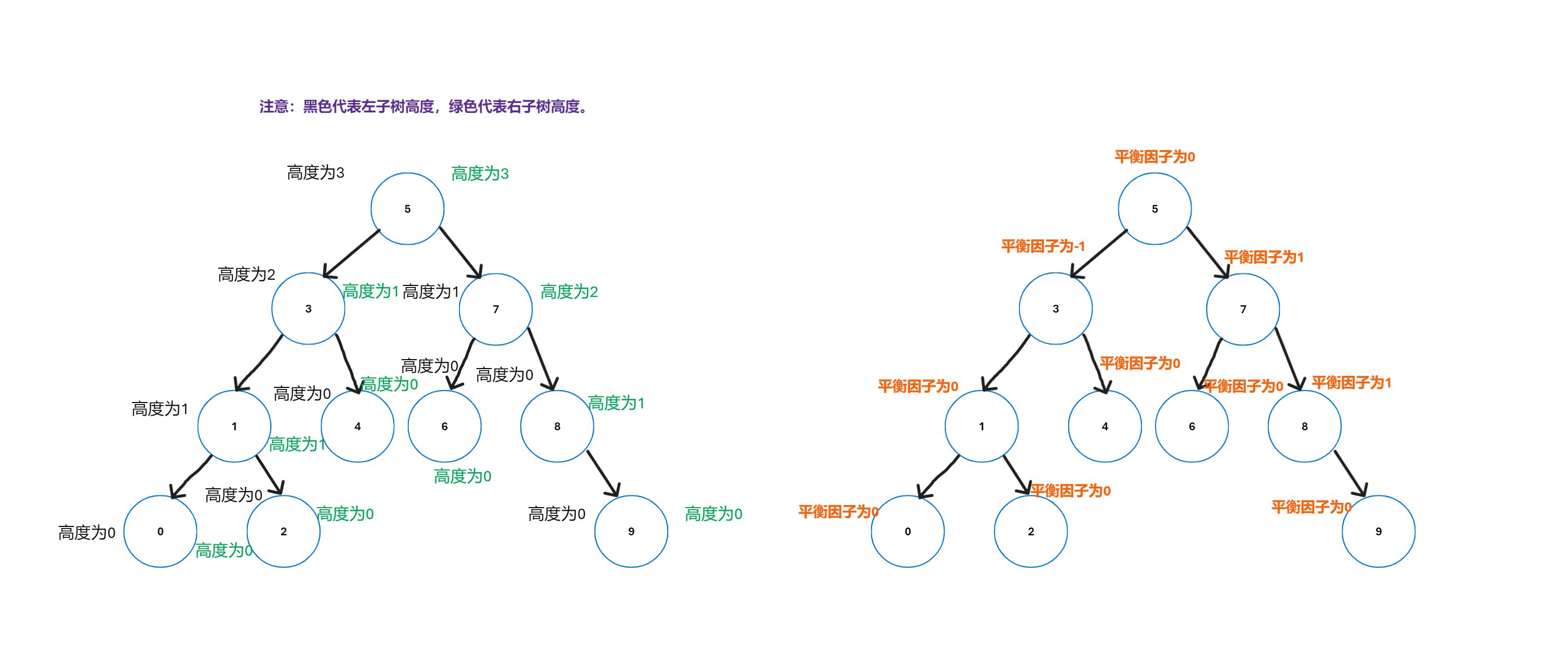
👨🏻💻AVL树的作用
我们已经了解到,AVL树的主要作用就是优化二叉搜索树当插入数据接近有序的时候查找的时间复杂度,从O(N) -> O(logN),例如当我们插如 1,2,3,4,5的时候 :
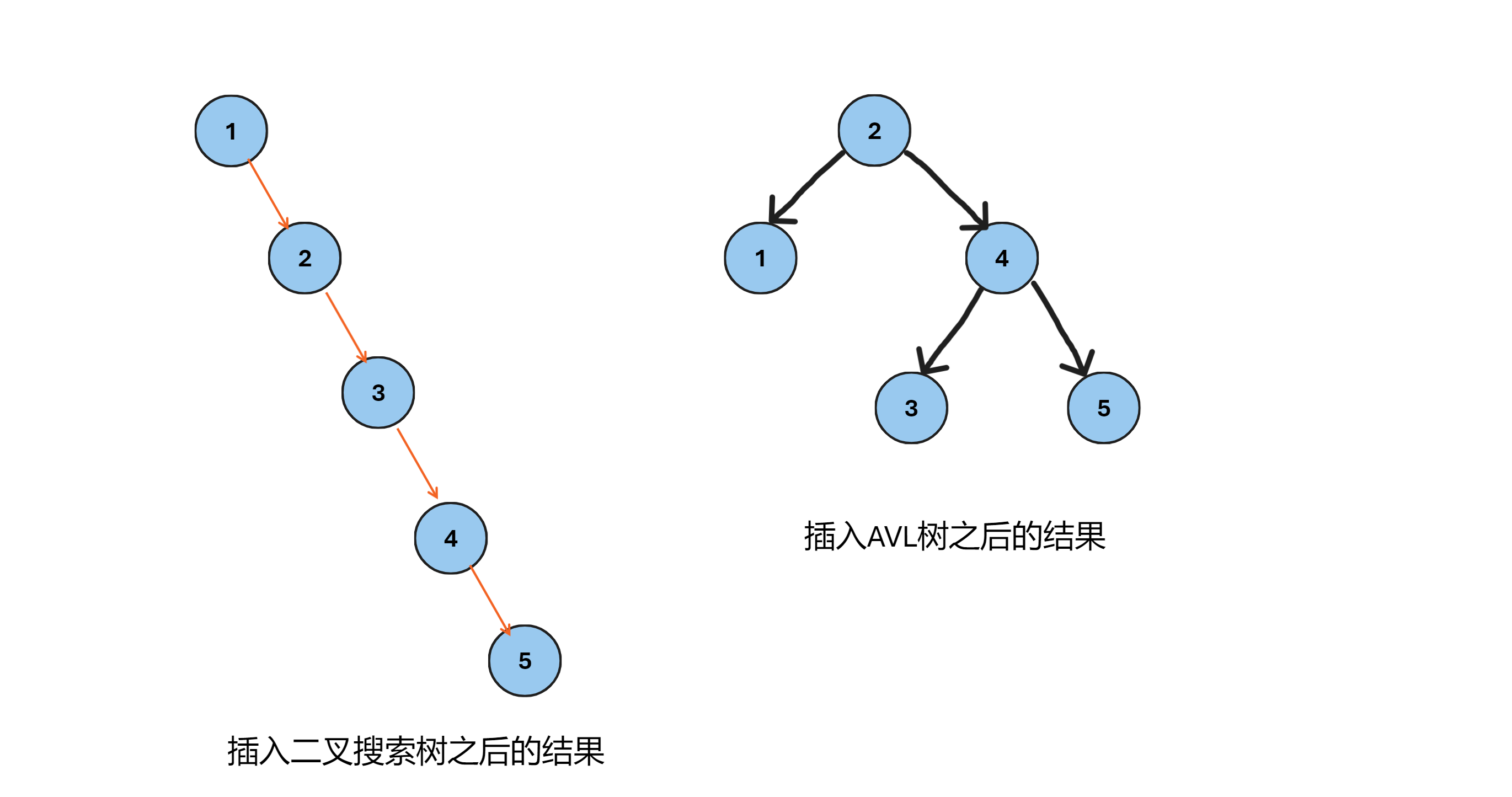
2. C++实现AVL树
👨🏻💻AVL树节点的定义
在每个节点中,应该有左右孩子的指针,指向父亲的指针(更新平衡因子时有用),平衡因子_bf,以及key和val(KV模型),用pair封装,代码如下:
template<class K, class V>
struct AVLTNode
{
typedef AVLTNode<K, V> Node;
Node* _left;
Node* _right;
Node* _parent;
pair<K, V> _kv;
int _bf;
AVLTNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
👨🏻💻AVL树节点的插入
插入的时候,大体思路还是和二叉搜索树类似,只是要更新平衡因子,怎么更新呢?插入一个节点,要更新所有它的父节点(有直系关系的节点,一直到根节点),如果插入的节点是它的右子树,平衡因子就加加,插入的节点是左子树,平衡因子就减减,那么平衡因子就会有以下几种情况:
_bf == 0,说明插入之前的_bf == 1 || _bf == -1,满足AVL树,不需要进行调整;_bf == 1 || _bf == -1,说明插入之前的_bf == 0,说明父节点的高度增加了,要继续往上更新;_bf == 2 || _bf == -2,不满足AVL树,要进行旋转调整,怎么旋转调整呢?待会再细说。- _bf 不可能大于2或者小于-2,因为当
_bf == 2的时候就会进行调整,使它的平衡因子变成0,至于为什么是0,调整的时候细说。
- _bf 不可能大于2或者小于-2,因为当
代码:
bool insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (kv.first > cur->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
// 更新所有它的父节点,一直到根节点
while (parent)
{
if (cur == parent->_left)
{
--parent->_bf;
}
else if (cur == parent->_right)
{
++parent->_bf;
}
// 平衡因子为0,说明插入之前parent的平衡因子为1或者-1,高度不变,不需要调整
if (parent->_bf == 0)
{
break;
}
// 平衡因子为正负1,说明插入之前的平衡因子为0,高度增加,要继续往上调整
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = cur->_parent;
}
// 平衡因子为正负2,要进行旋转调整
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 这里待会再实现
}
else
{
assert(false);
}
}
}
2.1 插入——左左型的右旋
👨🏻💻出现情况
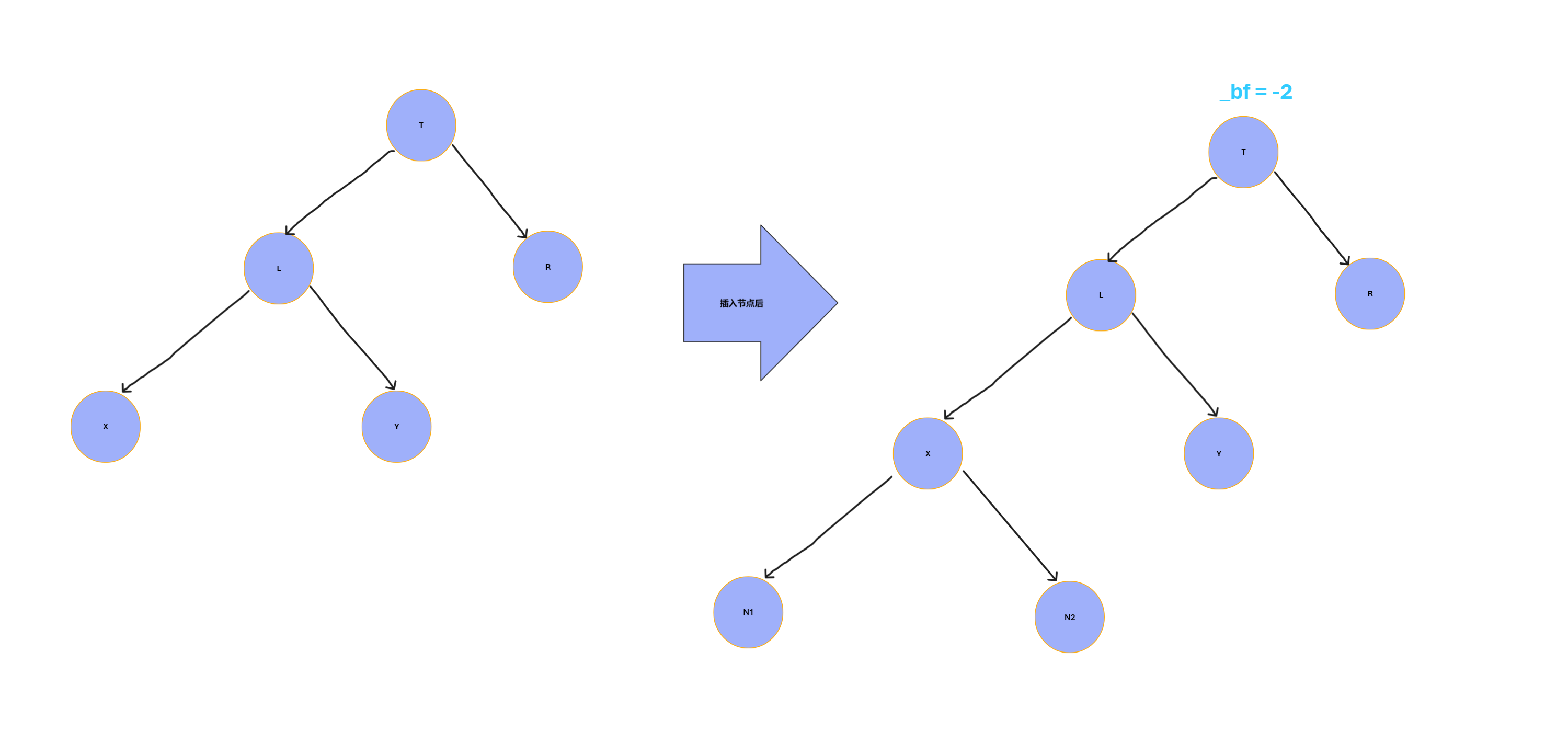
由图可见,插入之前满足AVL树的条件,插入之后根节点T的左右子树高度之差不再满足绝对值小于等于1,破坏了AVL树的规则,要对其进行旋转。
T是平衡因子大于1的节点,L是它的左节点,Y是L的右节点
在节点T的 左节点 的 左子树 上插入了一个节点,这种称之为 左左型,要进行右旋转。
👨🏻💻右旋具体步骤
- T向右旋转成为L的右子树;
- L的右子树成为T的左子树。
注:为什么可以这样旋转呢?
我们可以发现这样的一个大小关系:L < Y < T,因此我们发现旋转过后还是满足二叉搜索树的规则。
👨🏻💻图解如下:
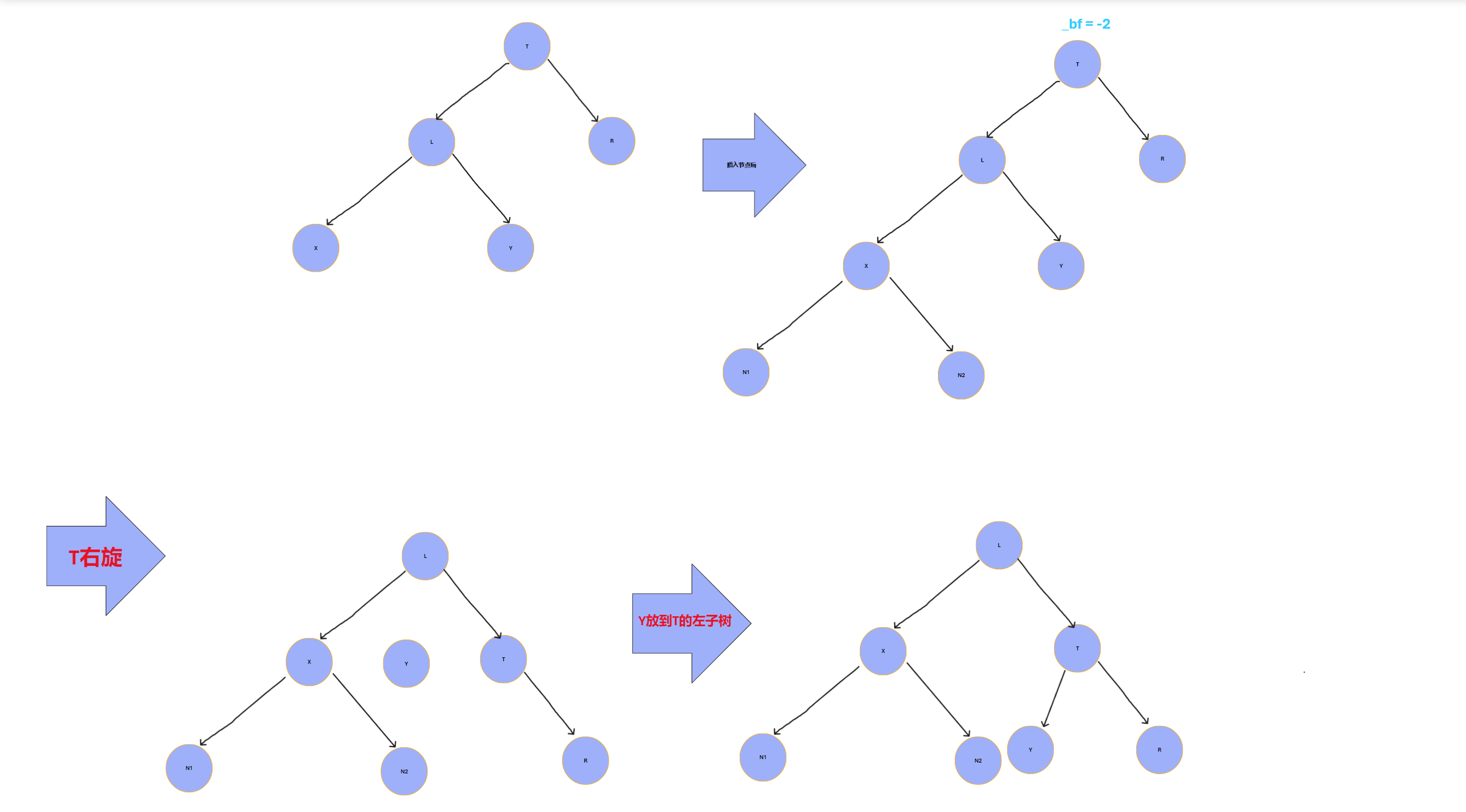
👨🏻💻右旋动画演示
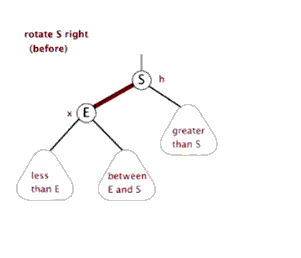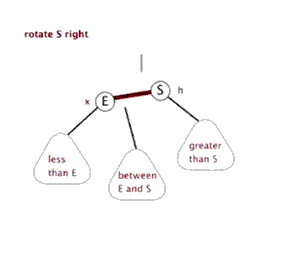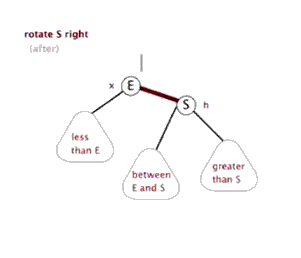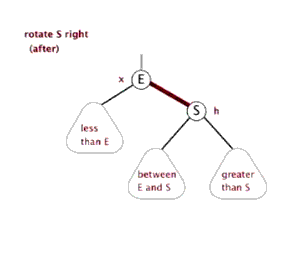
👨🏻💻右旋代码实现
这里看样子只需要改两个指针,但其实这两个指针牵扯到的其他指针也是很多的:
- 当把L的右孩子(Y)给T的时候也要改变Y的父指针,但是指向Y的指针可能为空,所以要特殊判断一下;
- 当L的右指针指向T的时候,要改变T的父指针,T可能本身就是根节点,那此时就要把L设置为根节点,并把T的父指针指向L;如果T不是根节点,就要记录T的父节点ppNode,并把L的父指针指向ppNode,把T的父指针指向L;
- 改变parent和L的平衡因子。
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
// 考虑为空的情况
if (subLR)
subLR->_parent = parent;
subL->_right = parent;
// 记录此时父亲的父节点的指向
Node* ppNode = parent->_parent;
parent->_parent = subL;
// 如果父节点为根节点
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
// 父节点不是根节点
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
subL->_parent = ppNode;
}
else
{
ppNode->_right = subL;
subL->_parent = ppNode;
}
}
// 更新平衡因子
parent->_bf = subL->_parent = 0;
}
2.2 插入——右右型的左旋
👨🏻💻出现情况
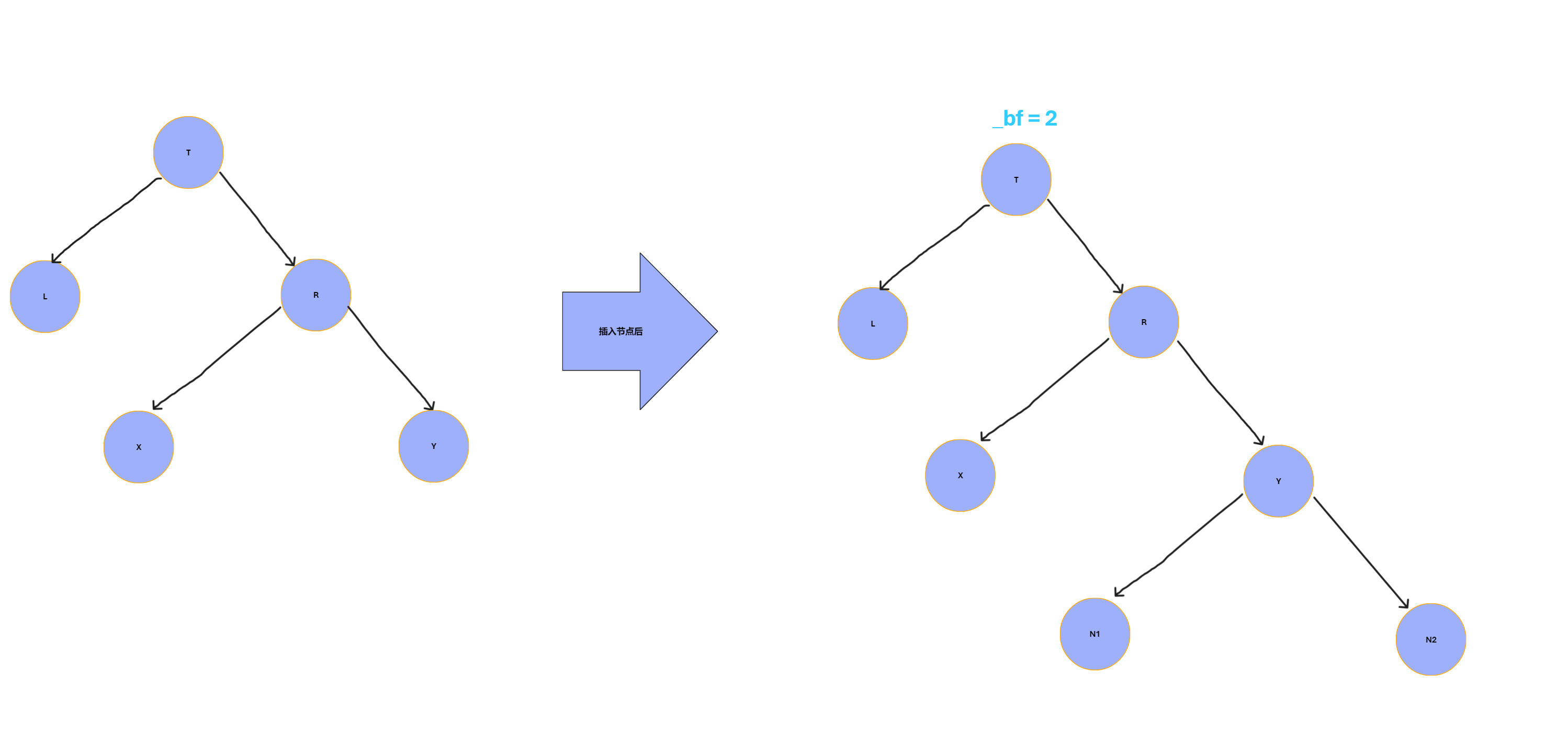
由图可见,插入之前满足AVL树的条件,插入之后根节点T的左右子树高度之差不再满足绝对值小于等于1,破坏了AVL树的规则,要对其进行旋转。
T是平衡因子大于1的节点,R是它的右节点,X是R的左节点
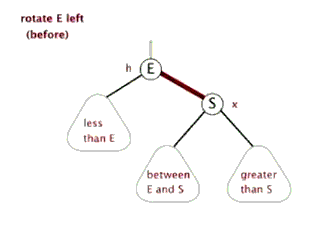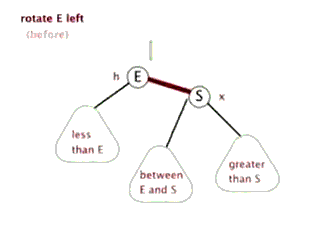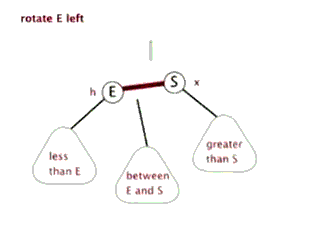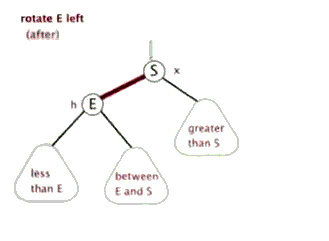
在节点T的 右节点 的 右子树 上插入了一个节点,这种称之为 右右型,要进行左旋转。
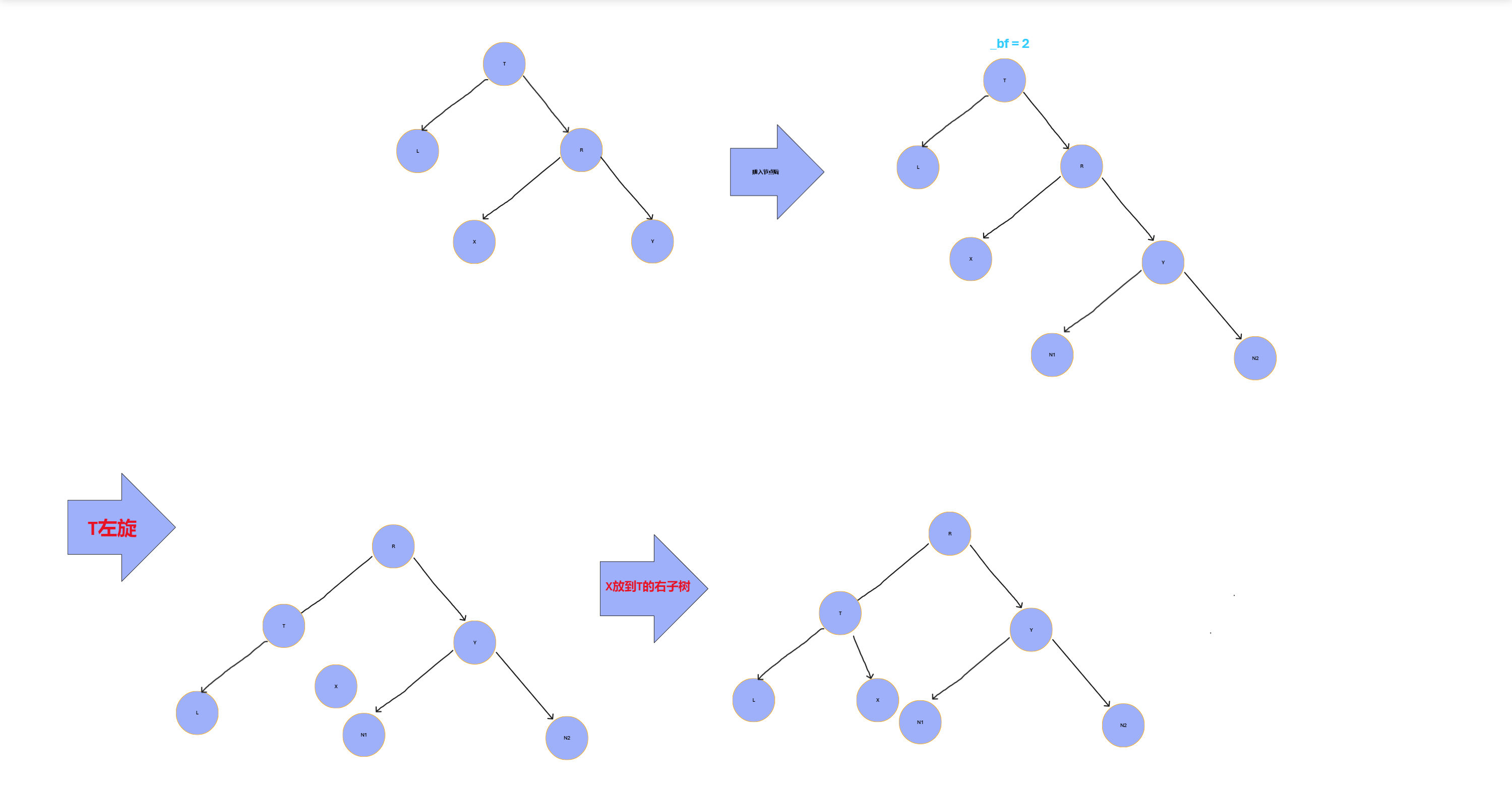
👨🏻💻左旋具体步骤
- T向左旋转称为R的左子树;
- R的左子树成为T的右子树。
注:为什么可以这样旋转呢?
我们可以发现这样的一个大小关系:T < X < R,因此我们发现旋转过后还是满足二叉搜索树的规则。
👨🏻💻图解如下:
👨🏻💻左旋动画演示
👨🏻💻左旋代码实现
这里要注意的点和右旋类似:
- 当把R的左孩子X给T的时候,要改变R的父指针的指向,但是X可能为空,所以要特殊判断一下;
- 当R的左孩子指向T的时候,要改变T的父指针的指向,T有可能是根节点,其父指针就是空,要把R设置为根节点,并改变T的父指针指向R;T如果不是根节点,此时就要记录其父节点ppNode,并把R的父指针指向ppNode,改变T的父指针指向R;
- 改变R和parent的平衡因子。
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
subR->_left = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
subR->_parent = ppNode;
}
else
{
ppNode->_right = subR;
subR->_parent = ppNode;
}
}
subR->_bf = parent->_bf = 0;
}
3. 总结
| 插入位置 | 状态 |
|---|---|
| 在结点T的左结点(L)的 左子树(L) 上做了插入元素 | 左左型,右旋 |
| 在结点T的右结点(R)的 右子树(R) 上做了插入元素 | 右右型,左旋 |