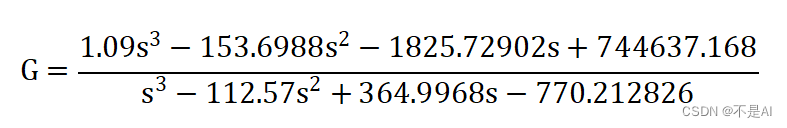一、转换式

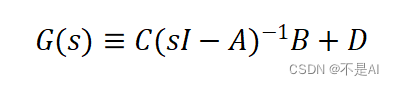
二、系统的状态空间模型

由矩阵A, B, C, D给出：

三、由状态空间模型转化为转换方程模型

函数原型（版权所有：scipy）：

def ss2tf(A, B, C, D, input=0):
    r"""State-space to transfer function.

    A, B, C, D defines a linear state-space system with `p` inputs,
    `q` outputs, and `n` state variables.

    Parameters
    ----------
    A : array_like
        State (or system) matrix of shape ``(n, n)``
    B : array_like
        Input matrix of shape ``(n, p)``
    C : array_like
        Output matrix of shape ``(q, n)``
    D : array_like
        Feedthrough (or feedforward) matrix of shape ``(q, p)``
    input : int, optional
        For multiple-input systems, the index of the input to use.

    Returns
    -------
    num : 2-D ndarray
        Numerator(s) of the resulting transfer function(s). `num` has one row
        for each of the system's outputs. Each row is a sequence representation
        of the numerator polynomial.
    den : 1-D ndarray
        Denominator of the resulting transfer function(s). `den` is a sequence
        representation of the denominator polynomial.

    Examples
    --------
    Convert the state-space representation:

    .. math::

        \dot{\textbf{x}}(t) =
        \begin{bmatrix} -2 & -1 \\ 1 & 0 \end{bmatrix} \textbf{x}(t) +
        \begin{bmatrix} 1 \\ 0 \end{bmatrix} \textbf{u}(t) \\

        \textbf{y}(t) = \begin{bmatrix} 1 & 2 \end{bmatrix} \textbf{x}(t) +
        \begin{bmatrix} 1 \end{bmatrix} \textbf{u}(t)

    >>> A = [[-2, -1], [1, 0]]
    >>> B = [[1], [0]]  # 2-D column vector
    >>> C = [[1, 2]]    # 2-D row vector
    >>> D = 1

    to the transfer function:

    .. math:: H(s) = \frac{s^2 + 3s + 3}{s^2 + 2s + 1}

    >>> from scipy.signal import ss2tf
    >>> ss2tf(A, B, C, D)
    (array([[1., 3., 3.]]), array([ 1.,  2.,  1.]))
    """
    # transfer function is C (sI - A)**(-1) B + D

    # Check consistency and make them all rank-2 arrays

from scipy.signal import ss2tf, TransferFunction

# Convert to transfer-function model
A = [[102.59, -8.23, 56.79], [0.00, 9.98, -1.39], [12.97, 55.91, 0.00]]
B = [[1.97], [-3.45], [19.90]]
C = [[0.00, 65.57, 9.81]]
D = 1.09

G = ss2tf(A, B, C, D)
print("Transfer Function G:", G)

四、转换结果

Transfer Function G: (array([[ 1.09000000e+00, -1.53698800e+02, -1.82572902e+03,
         7.44637168e+05]]), array([   1.      , -112.57    ,  364.9968  , -770.212826]))