一文看懂卷积神经网络CNN（1）

参考资料

一、神经网络

1、人脑神经网络

2、人工神经网络

3、神经网络的发展历史

二、前馈神经网络

1、神经元

（1）Sigmoid型函数

① Logistic函数

②Tanh函数

③两个函数形状对比

（2）ReLU函数

① 带泄露的ReLU函数（PReLU）

②ELU函数

③几种函数形状的对比

（3）Swish函数

（4）GELU函数

2、网络结构

（1）前馈网络

（2）记忆网络

（3）图网络

3、前馈神经网络

（1）补充：感知器

（2）通用近似定理

（3）应用到机器学习

（3）参数学习

4、反向传播算法

5、自动梯度计算

（1）基本原理

（2）工作流程

（3）两种主要的自动微分方法

6、优化问题

（1）非凸优化问题

（2）梯度消失问题

三、总结

参考资料

在学习过程中，主要以邱锡鹏老师《神经网络与深度学习》为主要学习思路，并辅助网上已有的学习资料和学习网站。【之所以自己出一个总结，也是为了看过以后形成一个总结，方便后续查询】

邱老师的书里已经给出了系统的知识体系，强烈推荐大家去学习。

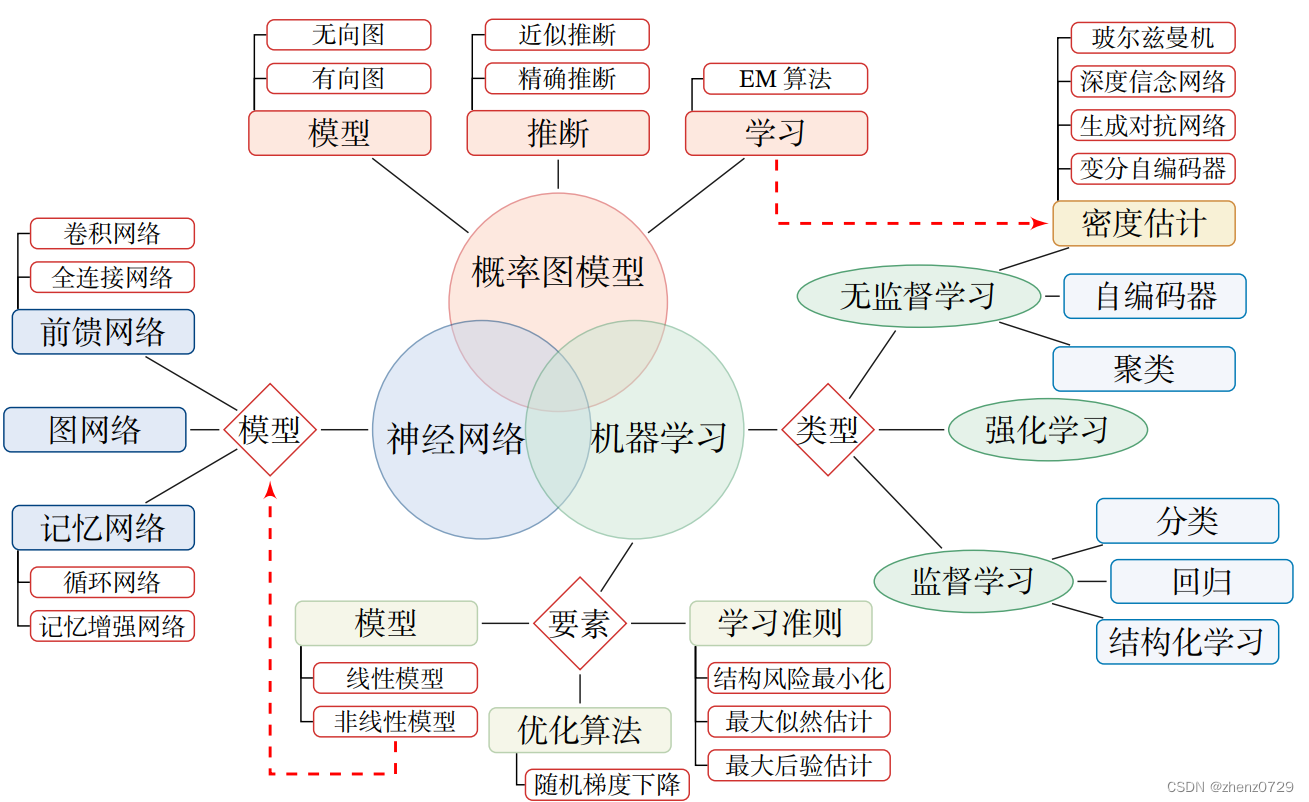
由于我主要学习目的就是CNN，所以只学神经网络—模型—前馈网络—卷积神经网络这个支线，如果有其他同学需要深度学习的，可以去看邱老师的书：https://nndl.github.io/nndl-book.pdf。

一、神经网络

神经网络是受人脑神经系统的启发，模拟人脑神经系统的数字模型，称为人工神经网络，简称神经网络。在机器学习领域，神经网络是指由很多人工神经元构成的网络结构模型，这些人工神经元之间的连接强度是可学习的参数。

1、人脑神经网络

神经元（Neuron），也叫神经细胞（Nerve Cell），是人脑中携带和传输信息的细胞，是人脑神经系统中最基本的单元。

每个神经元有上千个突触和其他神经元相连接。这些神经元和它们之间的连接形成巨大的复杂网络。

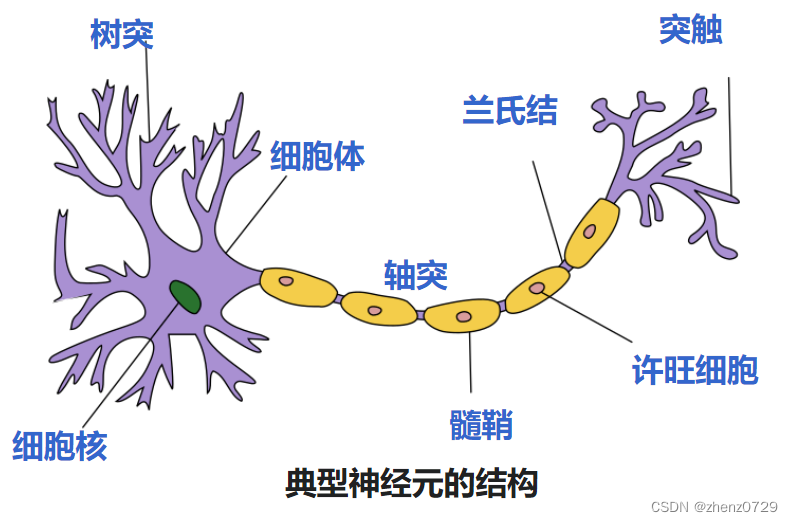
典型的神经元结构如下：

（1）细胞体（Soma）中的神经细胞膜上有各种受体和离子通道，胞膜的受体可与相应的化学物质神经递质结合，引起离子通透性及膜内外电位差发生改变，产生相应的生理活动：兴奋或抑制。

（2）细胞突起是由细胞体延伸出来的细长部分，又可分为树突和轴突：

树突（Dendrite）可以接收刺激并将兴奋传入细胞体。每个神经元可以有一或多个树突。
轴突（Axon）可以把自身的兴奋状态从胞体传送到另一个神经元或其他组织。每个神经元只有一个轴突。

神经元之间没有物理连接，但是可以向其他神经元收发信息。两个连接的神经元靠突触（Synapse）进行互联来传递信息，形成一个神经网络，即神经系统。突触可以理解为神经元之间的连接“接口”，将一个神经元的兴奋状态传到另一个神经元。一个神经元可被视为一种只有两种状态的细胞：兴奋和抑制。

神经元的状态取决于从其他的神经细胞收到的输入信号量，以及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会兴奋，产生电脉冲。电脉冲沿着轴突并通过突触传递到其他神经元。

在人脑神经网络中，不同神经元之间的突触有强有弱，其强度是可以通过学习（训练）来不断改变的，具有一定的可塑性。不同的连接形成了不同的记忆印痕。

突触可塑性原理：当神经元 A 的一个轴突和神经元 B 很近，足以对它产生影响，并且持续地、重复地参与了对神经元 B 的兴奋，那么在这两个神经元或其中之一会发生某种生长过程或新陈代谢变化，以致神经元 A 作为能使神经元B兴奋的细胞之一，它的效能加强了。

Hebb认为人脑有两种记忆：长期记忆和短期记忆。短期记忆持续时间不超过一分钟。如果一个经验重复足够的次数，此经验就可储存在长期记忆中。短期记忆转化为长期记忆的过程就称为凝固作用。

2、人工神经网络

人工神经网络是为模拟人脑神经网络而设计的一种计算模型，它从结构、实现机理和功能上模拟人脑神经网络。

人工神经网络由多个节点（人工神经元）互相连接而成，可以用来对数据之间的复杂关系进行建模。不同节点之间的连接被赋予了不同的权重，每个权重代表了一个节点对另一个节点的影响大小。每个节点代表一种特定函数，来自其他节点的信息经过其相应的权重综合计算，输入到一个激活函数中并得到一个新的活性值（兴奋或抑制）。

由于人工神经网络可以用作一个通用的函数逼近器（一个两层的神经网络可以逼近任意的函数），因此我们可以将人工神经网络看作一个可学习的函数，并将其应用到机器学习中。

3、神经网络的发展历史

第一阶段：模型提出

提出了许多神经元模型和学习规则；
提出了一种可以模拟人类感知能力的神经网络模型，称为感知器；
此时已经在应用领域（自动驾驶、模式识别等）取得了成效。

第二阶段：冰河期

哈佛大学的 Paul Werbos 发明反向传播算法；
受动物初级视皮层简单细胞和复杂细胞的感受野的启发，福岛邦彦提出了一种带卷积和子采样操作的多层神经网络：新知机（采用了无监督学习的方式来训练）。

第三阶段：反向传播算法引起的复兴

反向传播算法，简称BP算法，适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

第四阶段：流行度降低

神经网络可以很容易增加层数，神经元数量，从而构建复杂的网络，但是其计算复杂性也会随之增长，以当时的技术不足以支持训练大规模神经网络。

第五阶段：深度学习的崛起

Hinton通过逐层预训练来学习一个深度信念网络，并将其权重作为一个多层前馈神经网络的初始化权重，再用反向传播算法进行精调，这样可有有效解决深度神经网络难以训练的问题；
同时随着大规模并行计算以及GPU设备的普及，计算机的计算能力得以大幅提高，可供机器学习的数据规模也越来越大，计算机已经可以端到端训练一个大规模神经网络，不需要借助于训练的方式。

二、前馈神经网络

神经网络是一种打过莫的并行分布式处理器，从两个方面上模拟大脑：（1）网络获取的知识是通过学习来获取的；（2）内部神经元的连接强度，即突触权重，用来储存获取的知识。

神经网络有三个主要特性：（1）信息表示是分布式的（非局部的）；（2）基于和知识是储藏在单元之间的连接上的；（3）通过逐渐改变单元之间的连接强度来学习新知识。

从机器学习的角度来看，神经网络一般可以看作一个非线性模型，其基本组成单元为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得神经网络为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得神经网络称为一种高度非线性的模型。神经元之间的连接权重就是需要学习的参数，可以在机器学习的框架下通过梯度下降方法来进行学习。

1、神经元

人工神经元，简称神经元，是构成神经网络的基本单元，主要是模拟生物神经元的结果和特性，接收一组输入信号并产生输出。

一个生物神经元通常具有多个树突和一条轴突。树突用来接收信息，轴突用来发送信息。当神经元所获得的输入信号的积累超过某个阈值时，它就处于兴奋状态，产生电脉冲。轴突尾端有许多末梢可以给其他神经元的树突产生连接（突触），并将电脉冲信号传递给其他神经元。

假设一个神经元接收D个输入x1,x2,…,xp，令向量x=[x1;x2;…;;xp]来表示这组输入，并用净输入(Net Input)z€R表示一个神经元所获得的输入信号x的加权和：

其中的 $\omega$ 是D维的权重向量，b是偏置。

净输入z在经过一个非线性函数f(⋅)后，得到神经元的活性值a:

其中的非线性函数f(⋅)成为激活函数（Activation Function）.

为了增强网络的表示能力和学习能力，激活函数需要具备以下几点特质：

（1）连续并可导（允许少数点上不可导）的非线性函数．可导的激活函数可以直接利用数值优化的方法来学习网络参数；

（2）激活函数及其导函数要尽可能的简单，有利于提高网络计算效率；

（3）激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

（1）Sigmoid型函数

Sigmoid型函数是指一类S型曲线函数，为两端饱和函数．常用的Sigmoid型函数有Logistic函数和Tanh函数。

其实就是两端处，函数图形趋于直线。

① Logistic函数

函数定义为：

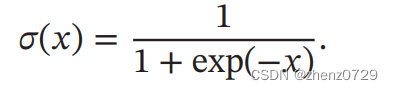
Logistic 函数可以看成是一个“挤压”函数，把一个实数域的输入“挤压”到 (0, 1)。当输入值在0附近时，Sigmoid型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制。输入越小，越接近于 0；输入越大，越接近于 1。

和感知器使用的阶跃激活函数相比，Logistic函数是连续可导的，其数学性质更好。

装备了Logistic激活函数的神经元具有以下两点性质：1）其输出直接可以看作概率分布，使得神经网络可以更好地和统计学习模型进行结合；2）其可以看作一个软性门（Soft Gate），用来控制其他神经元输出信息的数量。

②Tanh函数

函数定义：

Tanh函数可以看作放大并平移的Logistic函数，其值域是(−1, 1)。

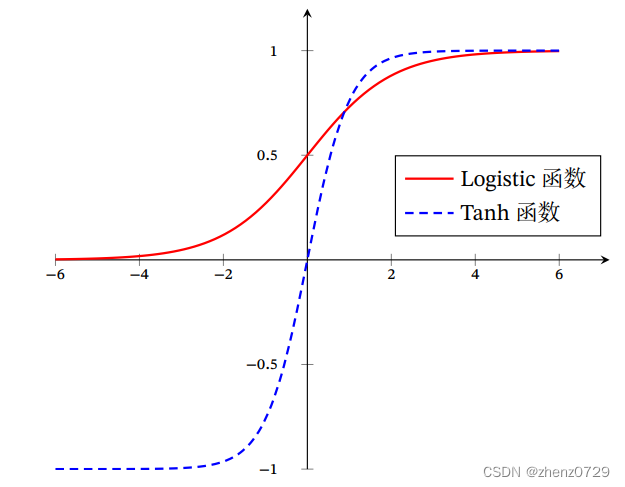
③两个函数形状对比

Tanh 函数的输出是零中心化的（Zero-Centered），而 Logistic 函数的输出恒大于 0。非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。

（2）ReLU函数

ReLU（Rectified Linear Unit，修正线性单元），也叫Rectifier函数，是目前深度神经网络中经常使用的激活函数。ReLU实际上是一个斜坡（ramp）函数，定义为：

【优点】

采用 ReLU 的神经元只需要进行加、乘和比较的操作，计算上更加高效。

Sigmoid 型激活函数会导致一个非稀疏的神经网络，而 ReLU 却具有很好的稀疏性，大约50%的神经元会处于激活状态。

在优化方面，相比于Sigmoid型函数的两端饱和，ReLU函数为左饱和函数，且在x > 0时导数为 1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。

梯度下降问题：是一种优化算法，用于训练神经网络模型。通过调整网络中的权重和偏置参数来最小化损失函数，从而达到学习数据模式的目的。（1）梯度的方向指向损失函数增长最快的方向。（2）通过不断迭代，沿着梯度的反方向更新参数，直到损失函数达到一个较小的值，或者达到预设的迭代次数。

【缺点】

死亡 ReLU 问题：在训练的时候，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU神经元在所有的训练数据上都不能被激活，说明这个神经元自身参数的梯度永远都为0，在以后得训练过程中永远不可能被激活。

① 带泄露的ReLU函数（PReLU）

在输入x<0时，保持一个很小的梯度 $\gamma$ ，当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不会激活。

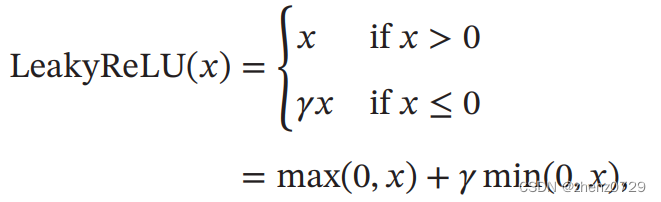
梯度 $\gamma$ 是一个很小的常数，当梯度 $\gamma$ <1时，带泄露的ReLU也可以写为：

（其实就是为了当输入为负时，ReLU的导数为0，导致神经元的权重在反向传播过程中不会更新，所以允许负输入有一个非零的梯度）

②ELU函数

ELU（Exponential Linear Unit，指数线性单元）是一个近似的零中心化的非线性函数。

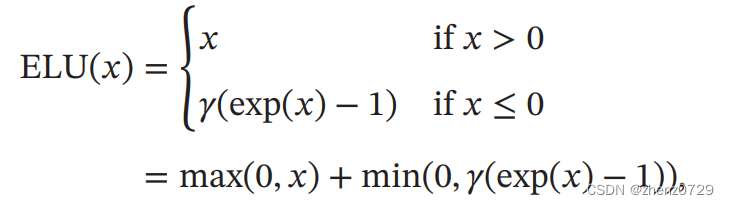
（ELU函数在负值区域的梯度随着输入值的减小而逐渐增大，这有助于梯度在深层网络中的传播，缓解了梯度消失的问题。ELU的负值部分的梯度是连续的，这有助于提高训练过程中的稳定性。）

③几种函数形状的对比

（3）Swish函数

是一种自门控的激活函数，由谷歌的研究人员在2017年提出。

其中，𝑥 是输入，𝜎是sigmoid函数，𝛽是一个可学习的参数或者一个固定的标量。Sigmoid函数的输出范围是(0, 1)，因此Swish函数的输出也是在输入𝑥的值乘以一个介于0到1之间的系数。

当𝜎(𝛽𝑥)接近于1时，门处于“开”状态，激活函数的输出近似于𝑥本身；
当𝜎(𝛽𝑥)接近于0时，门的状态为“关”，激活函数的输出近似于0。

当𝛽= 0时，Swish函数变成线性函数𝑥/2．当𝛽 = 1时，Swish函数在𝑥> 0 时近似线性，在𝛽 < 0 时近似饱和，同时具有一定的非单调性．当 𝛽 → +∞ 时， 𝜎(𝛽𝑥)趋向于离散的0-1函数，Swish函数近似为ReLU函数。

【优点】

Swish通过乘以一个由输入和𝛽β共同决定的系数来调整输入的值，这使得Swish能够根据输入的值自适应地调整其响应。
由于Swish函数中包含了sigmoid函数，因此它在整个实数域上都是连续且平滑的。
当输入𝑥x为负值时，Swish函数的输出会趋近于0，这引入了一定程度的稀疏性，有助于减少模型的复杂度。
当输入𝑥为负值时，Swish函数的输出会趋近于0，这引入了一定程度的稀疏性，有助于减少模型的复杂度。

（4）GELU函数

GELU（GaussianError Linear Unit，高斯误差线性单元）也是一种通过门控机制来调整其输出值的激活函数，和 Swish 函数比较类似。

其中P(X≤x)是标准正态分布的累积分布函数（CDF）。

【优点】

GELU的自适应性意味着它可以根据输入的值调整其激活程度，这有助于捕捉更复杂的特征。
GELU在整个定义域内都是平滑的，这有助于梯度的稳定传播。

2、网络结构

单一生物神经细胞功能比较简单，但是要模拟人脑能力，需要通过许多神经元一起协同来完成复杂的功能。这样通过一定的连接方式或信息传递方式进行协作的神经元可以看作一个网络，就是神经网络。

（1）前馈网络

前馈网络中各个神经元按接收信息的先后分为不同的组。每一组可以看作一个神经层。每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元。整个网络中的信息是朝一个方向传播，没有反向的信息传播，可以用一个有向无环路图表示。

前馈网络包括全连接前馈网络和卷积神经网络等。

前馈网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。这种网络结构简单，易于实现。

（2）记忆网络

记忆网络，也称为反馈网络，网络中的神经元不但可以接收其他神经元的信息，也可以接收自己的历史信息。和前馈网络相比，记忆网络中的神经元具有记忆功能，在不同的时刻具有不同的状态。和前馈网络相比，记忆网络中的神经元具有记忆功能，在不同的时刻具有不同的状态。

记忆网络包括循环神经网络、Hopffeld 网络、玻尔兹曼机、受限玻尔兹曼机等。

记忆网络可以看作一个程序，具有更强的计算和记忆能力。

为了增强记忆网络的记忆容量，可以引入外部记忆单元和读写机制，用来保存一些网络的中间状态，称为记忆增强神经网络。比如神经图灵机和记忆网络等。

（3）图网络

前馈网络和记忆网络的输入都可以表示为向量或向量序列。实际应用中，很多数据都是图结构的数据，比如知识图谱、社交网络等。前馈网络和记忆网络很难处理图结构的数据。

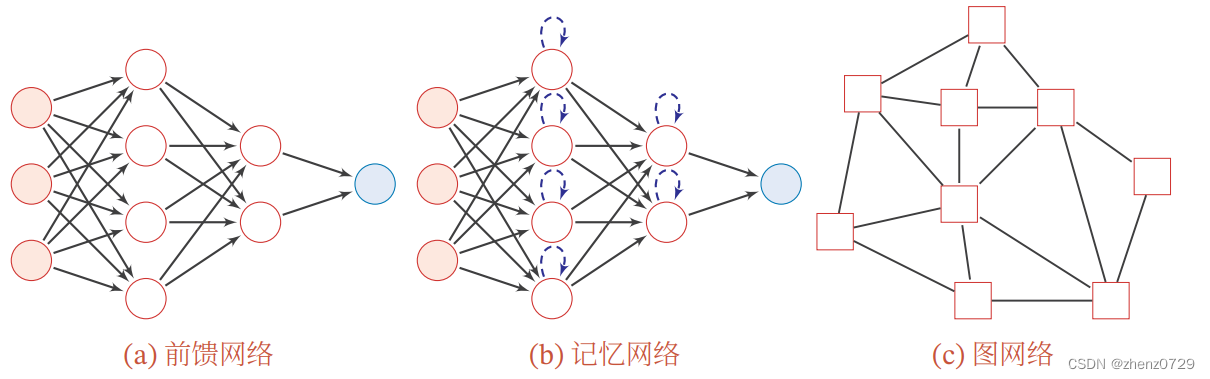
上图是三种不同的网络结构示例。可以看出，图网络是定义在图结构数据上的神经网络，图中每个节点都由一个或者一组神经元构成。神经元之间的连接可以是有向的，也可以是无向的。每个节点都可以接受来自相邻节点或自身的信息。

图网络是前馈网络和记忆网络的泛化，包含很多不同的实现方式，比如图卷积网络（Graph Convolutional Network，GCN）、图注意力网络（Graph Attention Network，GAT）、消息传递神经网络（Message Passing Neural Network，MPNN）等。

3、前馈神经网络

给定一组神经元，可以将神经元作为节点来构建一个网络。不同的神经网络模型有着不同网络连接的拓扑结构。一种比较直接的拓扑结构是前馈网络。

前馈神经网络（Feedforward Neural Network，FNN）是最早发明的简单人工神经网络。

前馈神经网络其实是由多层的 Logistic 回归模型（连续的非线性函数）组成，而不是由多层的感知器（不连续的非线性函数）组成。

在前馈神经网络中，各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。

下图是一个多层前馈神经网络。

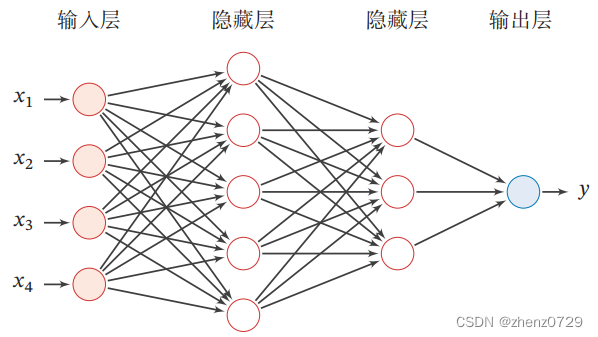
下表是前馈神经网络的记号。

所以首先需要根据第l-1层神经元的输出（活性值），计算出第l层神经元的净输入（净活性值），然后经过一个激活函数得到第l层神经元的活性值。

所以上述两个表达可以合并成：

或者：

所以按照这个顺序，前馈神经网络可以通过逐层的信息传递，得到网络最后的输出。整个网络可以作为一个复合函数，将输入的数据作为第一层的输入，将第L层的输出作为整个函数的输出。

（1）补充：感知器

感知器（Perceptron）是神经网络中最基本的单元，可以被看作是神经网络的“细胞”。它是一种简单的线性二分类模型，由美国科学家Frank Rosenblatt在1957年提出。感知器的设计灵感来源于生物神经系统，尤其是人脑神经元的工作方式。

感知器的基本结构包括：

输入：感知器可以接收多个输入信号x1,x2,...,xn。
权重：每个输入信号都有一个对应的权重𝑤1,𝑤2,...,𝑤𝑛，这些权重可以调整，用于控制输入信号对输出的影响。
偏置：感知器通常还有一个偏置项𝑏，它是一个常数，用于调整决策边界的位置。
激活函数：输入信号与权重的线性组合通过一个激活函数𝜎映射到输出。在最初的感知器模型中，使用的是阈值激活函数（也称为Heaviside函数或单位步阶函数）。

感知器的数学表达式如下：

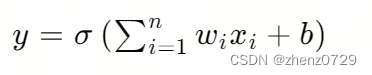
其中，y是感知器的输出，𝜎是激活函数，括号里是输入信号与权重的线性组合。

感知器的工作原理如下：

线性组合：首先，将每个输入信号乘以其对应的权重，然后求和，再加上偏置项，得到一个线性组合。
阈值决策：然后，将线性组合的结果输入到激活函数中。在最简单的情况下，激活函数是一个阈值函数，如果线性组合的结果大于0，则输出1（或者真），表示一个类别；如果小于等于0，则输出0（或者假），表示另一个类别。
分类决策：感知器的输出可以被解释为一个分类决策，用于区分输入信号属于两个类别中的哪一个。

感知器的特点包括：

简单性：感知器模型非常简单，易于理解和实现。
线性分类：感知器只能解决线性可分问题，即可以通过一个线性决策边界将输入空间划分为两个类别的问题。
在线学习：感知器可以使用一种称为“感知器学习规则”的在线学习算法进行训练，每次处理一个训练样本，逐步更新权重和偏置。
局限性：感知器的一个主要局限性是它只能模拟线性可分的函数，对于非线性问题，它的表现不佳。

尽管感知器在处理复杂问题时的能力有限，但它在机器学习和深度学习的发展历史中具有重要意义。感知器是许多现代神经网络模型的基础，并且它的一些概念和算法（如权重更新规则）被扩展和应用于更复杂的网络结构中。此外，感知器的一些变体和扩展（如多层感知器）可以解决更复杂的问题。

（2）通用近似定理

前馈神经网络具有很强的拟合能力，常见的连续非线性函数都可以用前馈神经网络来近似。

通用理解就是，只要有线性输出层和至少一个使用“挤压”性质的激活函数（像 Sigmoid 函数的有界函数）的隐藏层组成的前馈网络，只要其中隐藏层神经元数量足够多，则前馈神经网络可以以任意精度来近似任何一个定义在实数空间的有界闭集函数。

有界闭集函数是从一个集合到另一个集合的函数，它将输入集合中的闭集映射到输出集合中的有界闭集。

通用近似定理只是说明了神经网络的计算能力可以去近似一个给定的连续函数，但并没有给出如何找到这样一个网络，以及是否是最优的。所以在找最优映射函数时，一般是通过经验风险最小化和正则化进行参数学习。

（3）应用到机器学习

根据通用近似定理，神经网络在某种程度上可以作为一个“万能”函数来使用，可以用来进行复杂的特征转换，或逼近一个复杂的条件分布。

在机器学习中，要想取得好的分类效果，需要将样本的原始特征向量转换到更有效的特征向量，也就是特征抽取的过程。

多层前馈神经网络可以看成一个非线性复合函数 $\phi$ ，即将输入 $\chi$ 映射到输出 $\phi \left ( \chi \right )$ ，所以也能看成一种特征转换方法。

（3）参数学习

如果采用交叉熵损失函数，对于样本(x, y)，其损失函数为：

在机器学习和深度学习中，标签的one-hot向量表示是一种常用的编码方式，用于将分类变量转换为机器学习模型可以更有效处理的格式。

One-hot编码：One-hot编码是一种表示分类变量的方法，其中每个类别用一个二进制向量表示。这个向量的长度等于类别的总数，并且除了表示该类别的一个位置是1之外，其余位置都是0。这种表示方法称为“one-hot”，因为只有一个位置是“热”（即1），其余位置都是“冷”（即0）。

假设有一个简单的分类任务，目标是识别图片中的动物，可能的动物有猫、狗和鸟，总共3个类别。下面是各个类别的one-hot编码表示：

猫：[1, 0, 0]
狗：[0, 1, 0]
鸟：[0, 0, 1]

One-hot编码将分类标签转换为数值型格式，可以供多种大模型使用；避免了给类别赋予一个不恰当的数值顺序；one-hot编码可以扩展以允许单个样本同时属于多个类别。

其中W和b表示网络中所有的权重矩阵和偏置向量。||W||是正则化项，用来防止过拟合。 $\lambda$ >0为超参数， $\lambda$ 越大，W越接近于0。

过拟合（Overfitting）指的是模型在训练数据上表现得非常好，但是对于未见过的新数据（即测试数据或验证数据）泛化能力差的现象。即过拟合的模型在训练集上可能拥有很高的准确率，但在新数据上的表现却显著下降。

4、反向传播算法

假设采用随机梯度下降进行神经网络参数学习，给定一个样本 (x, y)，将其输入到神经网络模型中，得到网络输出为y'．假设损失函数为 ℒ(y, y')，要进行数学习就需要计算损失函数关于每个参数的导数。

（书里有推导过程，就不写了）

第l层的误差项为：

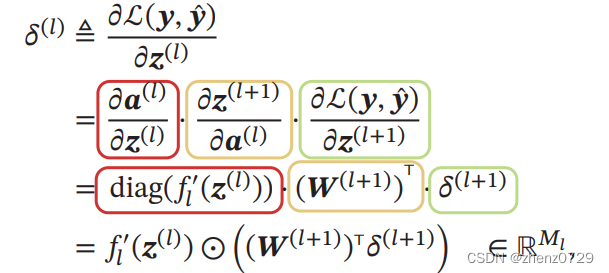
第l层的误差项可以通过第l+1层的误差项计算得到，这就是误差的反向传播。

反向传播算法利用梯度下降法来更新神经网络的权重，以最小化网络的预测误差。算法的基本步骤如下：

1. 初始化网络参数：在开始训练之前，需要初始化神经网络的权重和偏置。
2. 正向传播（Forward Pass）：对于给定的输入数据，按照从输入层到隐藏层再到输出层的顺序，计算每一层的输出。这个过程称为正向传播。在输出层，我们得到网络对当前输入的预测结果。
3. 计算损失（Loss Calculation）：使用损失函数（如均方误差、交叉熵等）计算网络预测值和真实值之间的误差。损失函数的选择取决于具体的任务（如分类、回归等）。
4. 反向传播（Backward Pass）：反向传播是反向传播算法的核心。它从输出层开始，沿着神经网络的连接反向传递误差信号。对于每个连接的权重，计算损失函数关于该权重的梯度。这个过程使用链式求导法则，即先计算最外层函数关于内层函数的导数，再计算内层函数关于变量的导数。
5. 更新权重（Weight Update）：利用计算得到的梯度，通过梯度下降法更新每个权重和偏置。更新的幅度由学习率决定。学习率是一个超参数，需要预先设定。
6. 迭代优化：重复上述步骤，直到网络的权重和偏置收敛到一个解，或者达到预设的迭代次数。

使用误差反向传播算法的前馈神经网络训练过程可以分为一下三步：

（1）前馈计算每一层的净输入和激活值，直到最后一层；

（2）反向传播计算每一层的误差项；

（3）计算每一层参数的偏导数，并更新参数。

5、自动梯度计算

神经网络的参数主要通过梯度下降来进行优化，当确定了风险函数以及网络结构后，就可以手动用链式法则来计算风险函数对每个参数的梯度，并用代码实现。

自动梯度计算，通常称为自动微分（Automatic Differentiation，简称AD），是一种计算数学函数导数（梯度）的方法。

（1）基本原理

自动微分通过将导数的计算转化为计算机程序的执行，从而避免手动求解导数。它利用了微积分中的链式法则，将复杂函数的导数分解为一系列简单函数导数的乘积。

（2）工作流程

正向传播：在正向传播阶段，计算模型的输出。这涉及到一系列函数的复合，例如在神经网络中，输入数据通过多个层的变换得到最终的输出。
计算损失：使用损失函数计算模型输出和真实值之间的差异，得到损失值。
反向传播：反向传播阶段，从损失值开始，利用链式法则递归地计算每个参数（权重和偏置）的梯度。这些梯度指示了如何调整参数以减少损失。
权重更新：使用计算得到的梯度来更新模型的权重，通常通过梯度下降或其变种方法。

（3）两种主要的自动微分方法

符号自动微分（Symbolic Differentiation）：这种方法在算法开始前就计算出整个函数的导数表达式。它适用于解析形式已知且结构固定的函数。符号自动微分通常用于解析式复杂的函数，如在符号计算和一些机器学习库中。
数值自动微分（Numeric Differentiation）：这种方法通过数值方法近似计算导数，常见的有前向差分和后向差分。数值自动微分在处理复杂函数或无法获得解析解的函数时很有用。
反向自动微分（Backward-mode Automatic Differentiation）：这是在深度学习中常用的一种技术，它从损失函数开始反向计算梯度。由于链式法则，这种方法在计算复杂函数的梯度时非常高效。