目录

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

5.完整程序

---

1.程序功能描述

       三维球体空间中光线反射模拟与三维点云提取matlab仿真。设置一个三维的椭球模型，作为墙壁，然后根据光线的反射原理，设计三维空间内，光线的反射效果。在三维系统中，光线反射本质是是曲面上每个点对应的切面的反射处理。每个反射点作为空间三维点云的坐标点，进行三维重建。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

3.核心程序

....................................................................
hold on;
colormap bone
Xss=[];
Yss=[];
Zss=[];
% 进行多次反射的循环计算与绘图
for i = 1:FS
    i% 显示当前反射次数
.........................................................
    %三维点云坐标提取
    Xss=[Xss,X_start];
    Yss=[Yss,Y_start];
    Zss=[Zss,Z_start];


    pause(0.1);
end
xlabel('X');
ylabel('Y');
zlabel('Z');

figure;
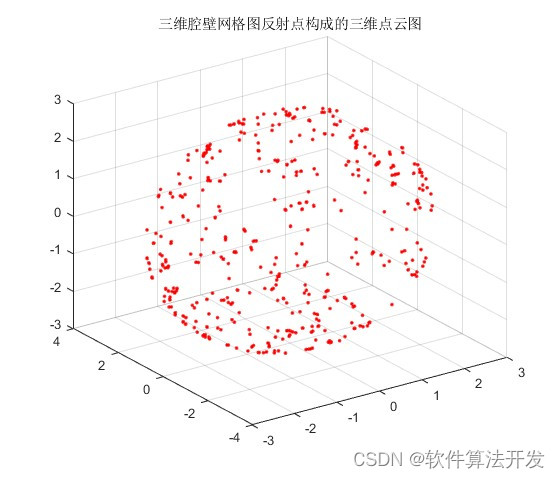
plot3(Xss,Yss,Zss,'r.');
grid on;
title('三维腔壁网格图反射点构成的三维点云图');




figure;
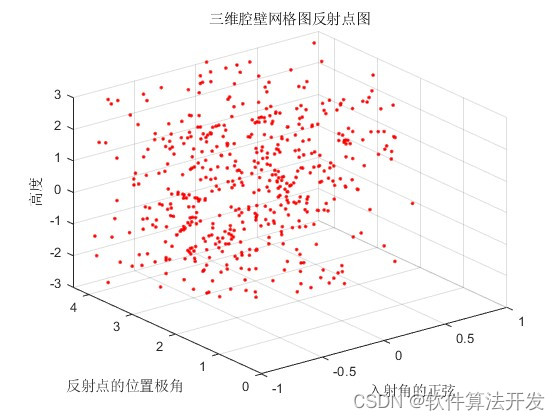
plot3(Xa,Xb,Xc,'r.');
xlabel('入射角的正弦');
ylabel('反射点的位置极角');
zlabel('高度');
grid on;
title('三维腔壁网格图反射点图');
 

figure;
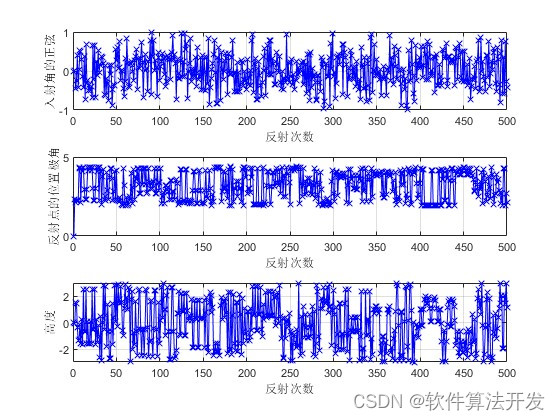
subplot(311)
plot(Xa,'b-x');
xlabel('反射次数');
ylabel('入射角的正弦');
grid on;
subplot(312)
plot(Xb,'b-x');
xlabel('反射次数');
ylabel('反射点的位置极角');
grid on;
subplot(313)
plot(Xc,'b-x');
xlabel('反射次数');
ylabel('高度');
grid on;


figure;
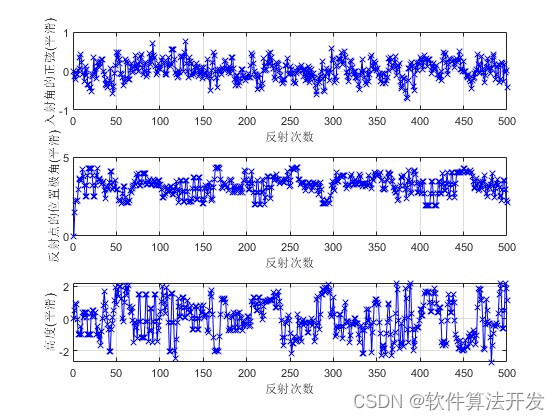
subplot(311)
plot(smooth(Xa,4),'b-x');
xlabel('反射次数');
ylabel('入射角的正弦(平滑)');
grid on;
subplot(312)
plot(smooth(Xb,4),'b-x');
xlabel('反射次数');
ylabel('反射点的位置极角(平滑)');
grid on;
subplot(313)
plot(smooth(Xc,4),'b-x');
xlabel('反射次数');
ylabel('高度(平滑)');
grid on;
24_004m

4.本算法原理

       在三维球体空间中模拟光线反射并进行三维点云提取是一个复杂的过程，涉及几何光学、光线追踪以及计算机图形学的多个领域。此过程不仅要求对光线与物体表面的交互有深刻理解，还需掌握点云数据的生成和处理技术。

       光线在三维空间中遇到表面时，遵循反射定律，即入射光线、反射光线和法线在同一平面内，且入射角等于反射角。入射角和反射角都是相对于法线（垂直于接触面的直线）测量的。

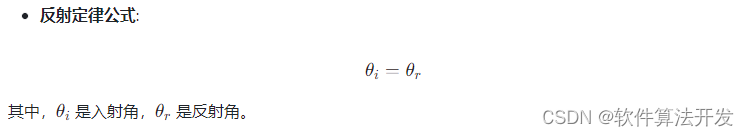
       光线追踪是一种渲染技术，通过追踪从视点出发的光线，模拟光线与场景中物体的交互（如反射、折射等），以计算像素的颜色。对于球体的反射，主要考虑镜面反射和漫反射两种情况。

       点云是表示三维物体表面的离散数据集合，每个点包含三维空间中的位置信息（x,y,z）及其他可能的属性（如颜色、强度）。在光线反射模拟中，可以通过追踪光线与球体表面的交点来生成点云数据。

      在真实场景中，光线可能在球体内经历多次反射。每次反射都需要重新计算反射方向，并判断反射后的光线是否再次与球体相交。这一过程需要递归进行，直到满足停止条件（如反射次数限制或光线离开场景）。

5.完整程序

VVV