一、不同路径I
62. 不同路径 - 力扣(LeetCode)


💡细节:
1.多开一行和一列(跟一维数组多开一个位置一样),这样方便初始化
2.状态转移方程:注意走一步并不是多一种走的路径,从i-1,j这个位置向下到i,j这个位置走一步,得出dp[i][j]为原来dp[i-1][j]条路径,而不是+1
3.初始化的时候得保证后面的结果是正确的:dp[0][1]=1或者dp[1][0]=1
代码:
class Solution {
public int uniquePaths(int m, int n) {
//细节1.多开一个行和一列:方便初始化
int[][] dp = new int[m+1][n+1];//dp[i][j]:到i,j位置有多少条路径
dp[0][1] = 1;//或者dp[1][0]=1
for (int i = 1; i <=m; i++) {
for (int j = 1; j <=n ; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m][n];
}
}二、不同路径II
63. 不同路径 II - 力扣(LeetCode)
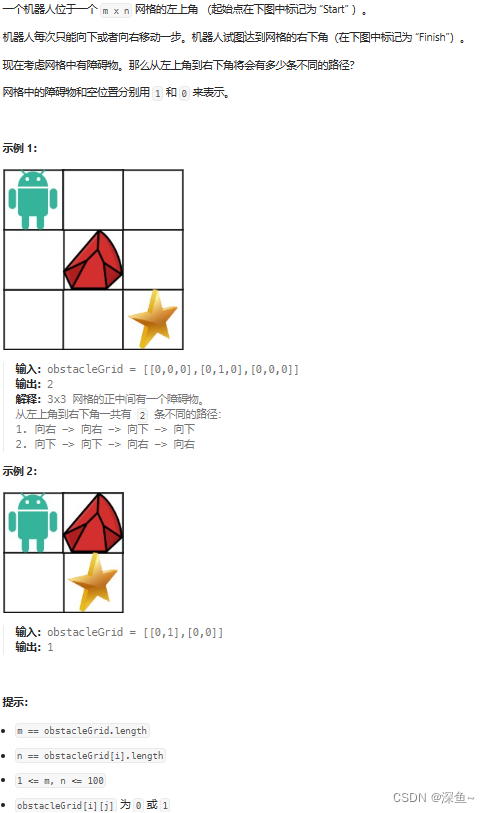
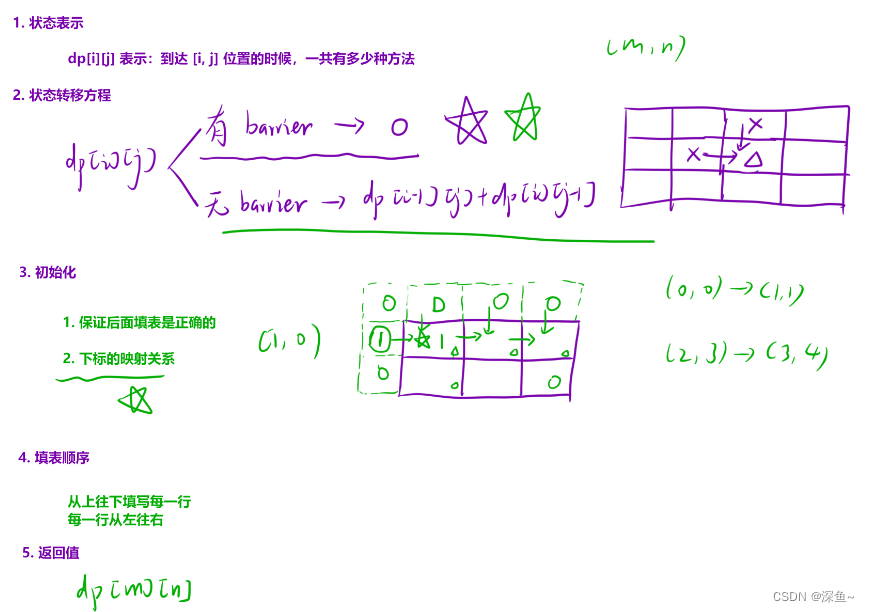
💡 细节:没有障碍物就正常相加,有障碍物那么dp[i][j]就为0,就不用管了
class Solution {
public int uniquePathsWithObstacles(int[][] ob) {
int m = ob.length;
int n = ob[0].length;
int[][] dp = new int[m+1][n+1];
dp[0][1] = 1;
for (int i = 1; i <=m ; i++) {
for (int j = 1; j <=n ; j++) {
if (ob[i-1][j-1]==0) {//没有障碍物就正常相加,有障碍物那么dp[i][j]就为0不用管
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
return dp[m][n];
}
}三、珠宝的最高价值
LCR 166. 珠宝的最高价值 - 力扣(LeetCode)

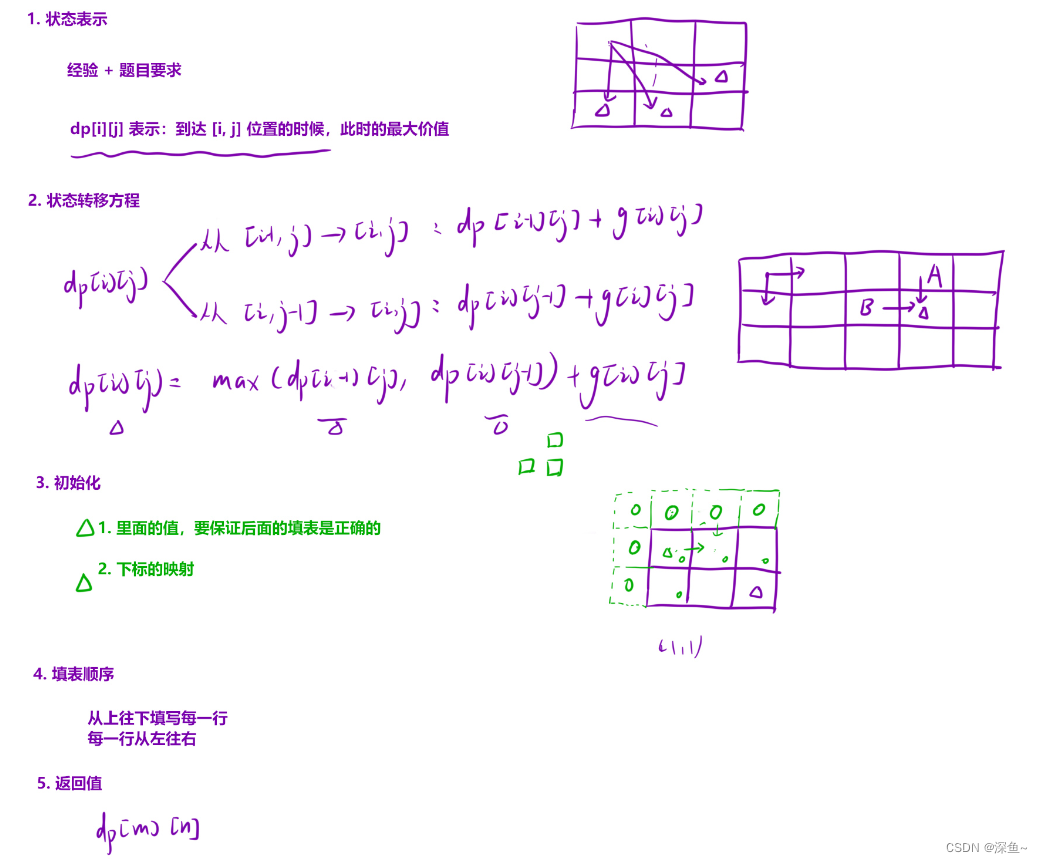
💡细节:注意下标的映射即可
class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length;
int n = frame[0].length;
int[][] dp = new int[m+1][n+1];//到达i,j位置拿到的珠宝价值
//初始化都为0即可
for(int i=1;i<=m;i++) {
for(int j=1;j<=n;j++) {
dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j])+frame[i-1][j-1];//注意下标的映射
}
}
return dp[m][n];
}
}四、下降路径的最小和
931. 下降路径最小和 - 力扣(LeetCode)

💡细节: 1.因为涉及了j+1,所以要多开两列
2.初始化注意:不能全部初始化为0,eg:在紫色2,1的位置,如果全为0,那么此位置的最小路径可能不正确
3.返回值不是一个位置的值,而是最后一行的最小值
class Solution {
public int minFallingPathSum(int[][] matrix) {
int m = matrix.length;
int[][] dp =new int[m+1][m+2];//多开一行,多开两列
//初始化:全部初始化为正无穷,然后第m一行为0
for (int i = 1; i < m+1; i++) {
dp[i][0] = dp[i][m+1] = Integer.MAX_VALUE;
}
for (int i = 1; i < m+1; i++) {
for (int j = 1; j < m+1; j++) {
dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];
}
}
int min = Integer.MAX_VALUE;
//返回值为最后一个的最小值
for (int i = 1; i < m+1; i++) {
min = Math.min(dp[m][i],min);
}
return min;
}
}五、最小路径和
64. 最小路径和 - 力扣(LeetCode)

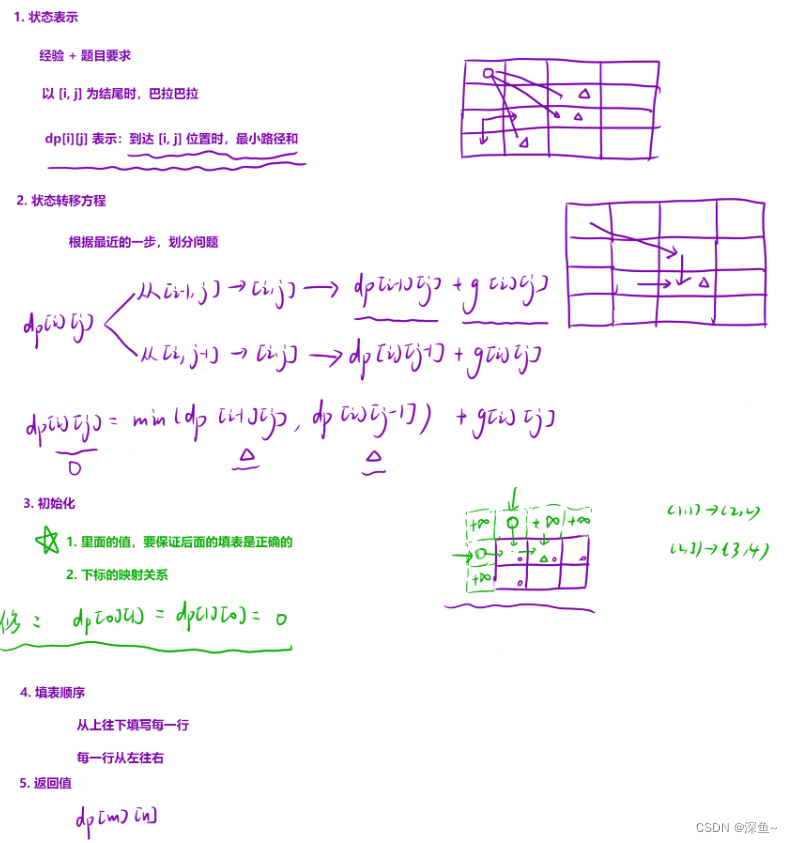
💡细节:初始化dp[0][1]和dp[1][0]为0,其余位置为正无穷即可
总结:扩展初始化的时候,一般找找min就全部设置为正无穷,找max就全部设置为负无穷,其他位置再来特别考虑
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m+1][n+1];
//初始化:扩展的部分全部初始化为正无穷,只有两个位置为0
for(int i=0;i<=n;i++) dp[0][i]=Integer.MAX_VALUE;
for(int i=0;i<=m;i++) dp[i][0]=Integer.MAX_VALUE;
dp[0][1] = dp[1][0] = 0;
for(int i=1;i<=m;i++) {
for(int j=1;j<=n;j++) {
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];//注意映射关系
}
}
return dp[m][n];
}
}六、地下城游戏
174. 地下城游戏 - 力扣(LeetCode)

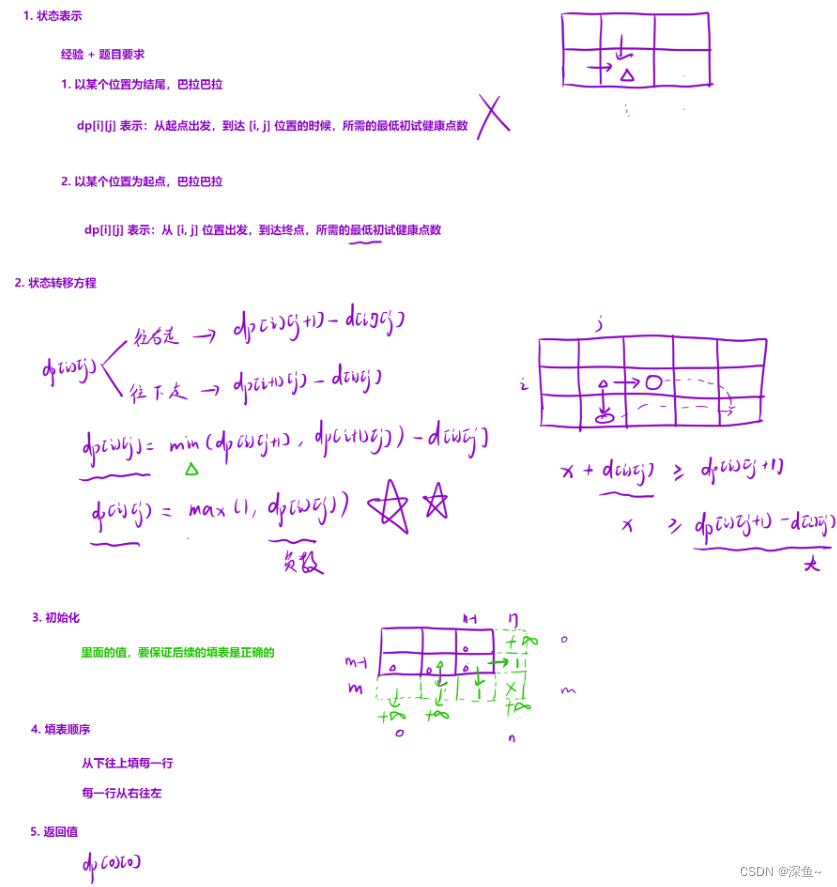
💡细节:1.dp表示不能像上面一样表示,因为以i,j位置为终点,每次都要重新确认最小健康证,所以不对就换成:从i,j这个位置到终点的最低的健康点数
2.初始化:这个拓展是在右下扩展,因为状态表示方程有j+1和i+1,初始化的时候都设置为正无穷,除了dp[m][n-1]和dp[m-1][n]为1,保证结果的正确性
3.状态表示:当前位置的健康值+dp当前位置 必须要大于等于 下一个位置的dp值
4.当dp[i][j]为负数的时候,根据dp表示的涵义,这个位置根本到不了,只能设置为1
class Solution {
//得保证最后的健康值为负的最大
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int[][] dp = new int[m+1][n+1];//dp[i][j]:从这个位置到终点所需的最低健康点数
//初始化:拓展的位置全部初始化为正无穷,只有dp[m][n-1]和dp[m-1][n]为1
for(int i=0;i<=n-1;i++) dp[m][i]=Integer.MAX_VALUE;
for(int i=0;i<=m-1;i++) dp[i][n]=Integer.MAX_VALUE;
dp[m][n-1] = dp[m-1][n] = 1;
for(int i=m-1;i>=0;i--)
{
for(int j=n-1;j>=0;j--)
{
dp[i][j] = Math.min(dp[i][j+1],dp[i+1][j])-dungeon[i][j];
dp[i][j] = Math.max(1,dp[i][j]);
}
}
return dp[0][0];
}
}