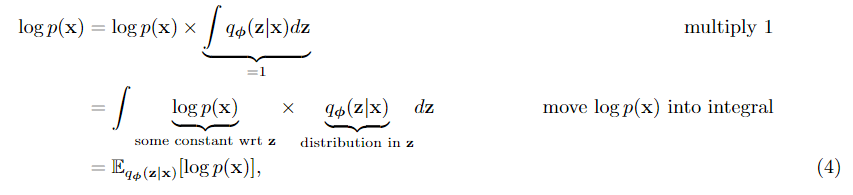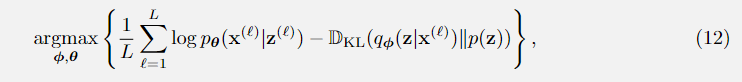1.The Basics: Variational Auto-Encoder
1.1 VAE Setting

自动编码器有一个输入变量x和一个潜在变量z
Example. 获得图像的潜在表现并不是一件陌生的事情。回到jpeg压缩,使用离散余弦变换(dct)基φn对图像的底层图像/块进行编码。如果你给我们一个imagex,我们会给你一个系数向量z。从z我们可以做逆变换来恢复(即解码)图像。因此,系数向量z是潜在码。编码器是dct变换,解码器是逆dct变换
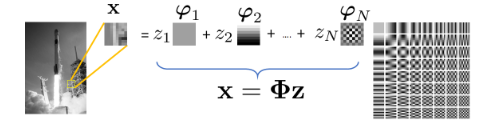
变分 variational 这个名字来源于我们用概率分布来描述x和z的因子。我们更感兴趣的不是求助于将x转换为z的确定性过程,而是确保分布p(x)可以映射到所需的分布p(z),并向后返回到p(x)
- p(x):x的分布。如果我们知道的话,我们早就成为亿万富翁了。整个星系的扩散模型都是为了找到从p(x)中提取样本的方法
- p(z):潜在变量的分布。因为我们都很懒惰,所以让我们把它设为零均值单位方差高斯p(z)=n(0,i)
- p(z|x):与编码器相关的条件分布,它告诉我们给定x时z的可能性,我们无法访问它。P (z|x)本身不是编码器,但编码器必须做一些事情,以便它与P (z|x)保持一致
- p(x|z):与解码器相关的条件分布,它告诉我们在给定z的情况下得到x的后验概率,同样,我们无法访问它。
Example.
考虑根据高斯混合模型分布的随机变量x,其中潜变量z∈{1,…,k}表示簇恒等式,使得 for k=1...k.我们假设
。那么,如果我们被告知只需要看第k个簇,给定z的x的条件分布是
x的边际分布可以用总概率定律找到
因此,如果我们从px(x)开始,编码器的设计问题是构建一个神奇的编码器,使得对于每个样本x~px(x,潜在编码将是z∈{1,…,k},分布为z~pz(k)。为了说明编码器和解码器是如何工作的,让我们假设均值和方差是已知的并且是固定的。否则,我们将需要通过em算法来估计均值和方差。这是可行的,但繁琐的方程会破坏本说明的目的
Encoder:我们如何从x中获得z?这很容易,因为在编码器处,我们知道px(x)和z(k)。假设你只有两个类z∈{1,2}。实际上,你只是在做一个二进制决定,决定样本x应该属于哪里。有很多方法可以做二进制决定。最大后验maximum-a-posteriori: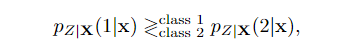
Decoder:在解码器方面,如果我们得到一个潜在代码z∈{1,…,k},神奇的解码器只需要返回一个样本x,它是从中提取的。不同的z将给出k个混合物组分中的一个。如果我们有足够的样本,总体分布将遵循高斯混合。
如果我们想找到神奇的编码器和解码器,我们必须有办法找到这两个条件分布
在vae的文献中,人们提出了一个考虑以下两种代替分布 proxy distributions 的想法:
:p(z|x)的代理。我们将使它成为高斯。为什么是高斯的?没有特别好的理由。
:p(x|z)的代理。信不信由你,我们也会把它变成高斯的。但这个高斯的作用与高斯
略有不同。虽然我们需要估计高斯
的均值和方差,但我们不需要估计高斯
的任何值。相反,我们将需要一个解码器神经网络来将z转换为x。高斯
将用于通知我们生成的图像x有多好。
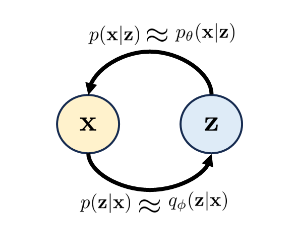
“正向 forward ”关系由p(z|x)指定(并由qφ(z|x)近似),而“反向”关系由p(x|z)指定(且由pθ(x|z)近似)。
Example.
假设我们有一个随机变量x和一个潜变量z:
我们的目标是建造一个VAE。(什么?!这个问题有一个平凡的解,其中z=(x−μ)/σ,x=μ+σz。你是绝对正确的。但请遵循我们的推导,看看VAE框架是否合理。)

我们的意思是要构造两个映射“encode”和“decode”。为了简单起见,我们假设这两个映射都是仿射变换 affine transformations:
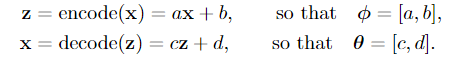
我们懒得找出联合分布p(x,z),也懒得找出条件分布p(x|z)和p(z|x)。但我们可以构造代理分布qφ(z|x)和pθ(x|z)。既然我们可以自由选择qφ和pθ应该是什么样子,那么我们考虑下面两个高斯如何
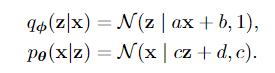
对于qφ(z|x):如果给定x,我们当然希望编码器根据我们选择的结构对分布进行编码。由于编码器结构是ax+b,所以qφ(z|x)的自然选择是具有平均值ax+b。方差被选择为1,因为我们知道编码样本z应该是单位方差。
类似地,对于pθ(x|z):如果我们给定z,解码器必须采用cz+d的形式,因为这就是我们设置解码器的方式。方差是c,这是我们需要计算的一个参数。
1.2 Evidence Lower Bound
我们如何使用这两个代理分布来实现确定编码器和解码器的目标?如果我们将φ和θ作为优化变量,那么我们需要一个目标函数(或损失函数),以便我们可以通过训练样本来优化φ和θ。为此,我们需要建立一个关于φ和θ的损失函数。我们在这里使用的损失函数被称为证据下界 Evidence Lower BOund(ELBO)

让我们看看elbo是什么意思以及它是如何派生的
简而言之,elbo是先前分布log p(x)的下界,因为我们可以证明

其中不等式源自kl散度总是非负的事实。因此,elbo是logp(x)的有效下界。由于我们从来没有访问过logp(x),如果我们以某种方式访问过elbo,并且elbo是一个很好的下界,那么我们可以有效地最大化elbo,以实现最大化logp(x)的目标,这是黄金标准。
正如你从方程和图2中看到的,当我们的代理qφ(z|x)可以精确地匹配真实分布p(z|x)时,不等式将变成等式。因此,游戏的一部分是确保qφ(z|x)接近p(z|x)。

Proof of Eqn (3).
这里的全部技巧是使用我们的神奇代理qφ(z|x)来绕过p(x)并导出边界。
最后一个等式:
对于任意随机变量Z和标量a,有
我们已经得到了方程
。只需多走几步。让我们使用bayes定理,该定理指出
:
我们现在有elbo。但是这个elbo仍然不太有用,因为它涉及p(x,z),这是我们无法访问的
让我们仔细看看elbo: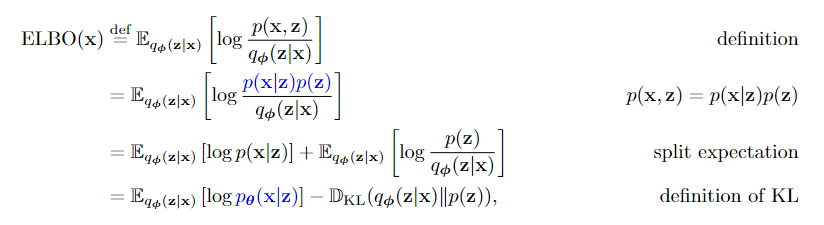
其中我们不可访问的p(x|z)替换为其代理

在方程(6)中存在两个项:
- Reconstruction 重建:关于解码器,如果我们将潜在的z馈送到解码器中,我们希望解码器产生好的图像x。因此,我们希望最大化log pθ(x|z)。它类似于最大似然,其中我们想要找到模型参数以最大化观察图像的似然。这里的期望是关于样本z(以x为条件)而取的。这并不奇怪,因为样本z用于评估解码器的质量。它不能是任意的噪声矢量,而是有意义的潜在矢量。因此,z需要从
中采样
- Prior Matching 先验匹配:第二项是编码器的kl散度。我们希望编码器将x转换为潜在向量z,这样潜在向量将遵循我们选择的分布
。为了更一般,我们将p(z)写为目标分布。因为kl是一个距离(当两个分布变得更不相似时它会增加),我们需要在前面加一个负号,这样当两个分布变得更相似时它就会增加
Example.
我们从之前的推导中知道

为了确定θ和φ,我们需要最小化先验匹配误差并最大化重建项。对于先前的匹配,我们知道
![]() ,
,![]()
![]() 使KL散度最小,因此,
使KL散度最小,因此,![]()
对于reconstruction项,我们知道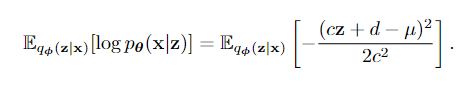
由于e[z] = 0, var[z] = 1,因此当c = σ, d = μ时,项最大(负的项分数最小)。综上所述,编码器和解码器参数为
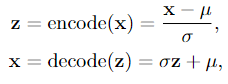
重构项和先验匹配项如图3所示。在这两种情况下,在训练过程中,我们假设我们可以访问z和x,其中z需要从qφ(z|x)中采样。然后,对于重建,我们估计θ以最大化pθ (x|z)。对于先验匹配,我们找到φ以最小化kl散度。优化可能具有挑战性,因为如果更新φ,分布qφ(z|x)将发生变化

1.3 Training VAE
既然我们理解了elbo的含义,我们就可以讨论如何训练vae了。为了训练vae,我们需要地面真值对(x,z)。我们知道如何得到x;它只是来自数据集的图像。但相应地,z应该是什么?
让我们来谈谈编码器。我们知道z是由分布qφ(z|x)生成的。我们还知道qφ(z|x)是高斯的。假设这个高斯有一个均值μ和一个协方差矩阵(哈!又是我们的懒惰!我们不使用一般的协方差矩阵,而是假设方差相等)。
棘手的部分是如何从输入图像x中确定μ和。我们构建了一个深度神经网络,这样

因此,样本z(ℓ)(ℓ 表示训练集中的第ℓ个训练样本)可以从高斯分布中采样
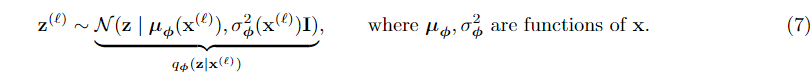
这个想法总结在图4中,我们使用神经网络来估计高斯参数,并从高斯中提取样本。注意 和
是x的函数(ℓ). 因此,对于不同的
我们将有一个不同的高斯

Remark.
对于任何高维高斯分布
,采样过程都可以通过白噪声的变换来完成
半矩阵 half matrix
可以通过特征分解或cholesky分解得到。对于对角矩阵
,以上简化为
我们来谈谈解码器。该解码器通过神经网络实现。为简便起见,我们将其定义为,其中θ表示网络参数。解码器网络的工作是取一个潜在变量z并生成一个图像
:
![]()
现在让我们再做一个(疯狂的)假设:解码图像和真实图像x之间的误差是高斯分布的。(等等,又是高斯分布?!)我们假设:
![]()
那么,可以得出分布pθ (x|z)为

D是x的维数
这个方程表明,elbo中似然项的最大值实际上就是解码图像和真实图像之间的l2损失。其思想如图5所示。

1.4 Loss Function
一旦你理解了编码器和解码器的结构,损失函数就很容易理解了。我们通过蒙特卡罗模拟近似期望:

其中是训练集中的第L个样本,
是从
采样的,分布qθ是
![]()
Training loss of VAE:
其中
为训练数据集中的地面真值图像,
从式(7)中采样。
kl散度项中的z不取决于ℓ 因为我们正在测量两个分布之间的kl散度。这里的变量z是一个伪变量。
我们需要澄清的最后一点是kl散度。由于![]() 和
和![]() ,我们本质上得到两个高斯分布;如果你去维基百科,你可以看到两个d维高斯分布
,我们本质上得到两个高斯分布;如果你去维基百科,你可以看到两个d维高斯分布![]() 的kl散度是
的kl散度是
 通过考虑
通过考虑![]() 我们可以证明kl散度有一个解析表达式
我们可以证明kl散度有一个解析表达式
![]() 其中d是向量z的维数。因此,总损失函数eqn(12)是可微的。因此,我们可以通过反向传播梯度来端到端地训练编码器和解码器
其中d是向量z的维数。因此,总损失函数eqn(12)是可微的。因此,我们可以通过反向传播梯度来端到端地训练编码器和解码器
1.5 Inference with VAE
为了进行推理,我们可以简单地将潜在向量z(从采样)放入解码器
中,得到图像x;见图6。


2 Denoising Diffusion Probabilistic Model (DDPM)
您只需要了解以下摘要:
扩散模型是增量更新,其中整体的组装为我们提供了编码器-解码器结构。从一种状态到另一种状态的转换是通过去噪器实现的。