标签

• 树
• 深度优先搜索
• 递归

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡的二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

原题：LeetCode 110.平衡二叉树

思路及实现

方法一：自顶向下递归（纯递归）

思路

定义函数 height\texttt{height}height，用于计算二叉树中的任意一个节点 ppp 的高度：

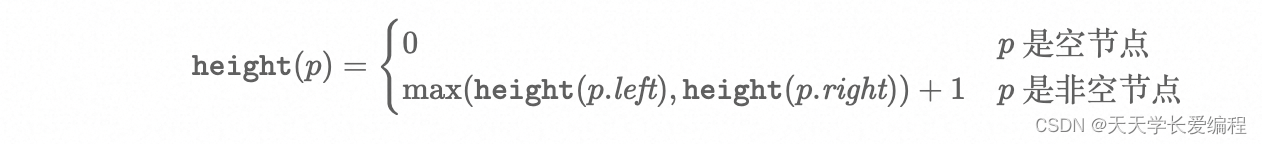
为了判断二叉树是否平衡，我们可以采用一个自顶向下的递归方法。该方法通过计算每个节点左右子树的高度差，并与 1 进行比较来判断当前子树是否平衡。如果当前子树平衡，则继续递归检查其子节点。

代码实现

Java版本

class Solution {  
  
    // 判断二叉树是否平衡  
    public boolean isBalanced(TreeNode root) {  
  
        // 如果根节点为空（即树为空），则树是平衡的  
        if (root == null) {  
            return true;  
        }  
        // 否则，判断当前节点的左右子树高度差是否不超过1，并且左右子树都是平衡的  
        else {  
            return Math.abs(height(root.left) - height(root.right)) <= 1 &&   
                   isBalanced(root.left) && // 递归判断左子树是否平衡  
                   isBalanced(root.right);  // 递归判断右子树是否平衡  
        }  
  
    }  
  
    // 计算树的高度  
    public int height(TreeNode root) {  
  
        // 如果根节点为空（即树为空或到达叶子节点的下一层），则返回高度为0  
        if (root == null) {  
            return 0;  
        }  
        // 否则，返回当前节点左子树和右子树中的较大高度加1（当前节点的高度为其子树的最大高度加1）  
        else {  
            return Math.max(height(root.left), height(root.right)) + 1;  
        }  
  
    }  
  
    // TreeNode类（假设已经在外部定义）  
    // class TreeNode {  
    //     int Val;  
    //     TreeNode Left;  
    //     TreeNode Right;  
    //     TreeNode(int val) { Val = val; }  
    // }  
  
}

说明：isBalanced 方法检查树是否平衡，同时递归地计算左右子树的高度。height 方法返回树的高度。

C语言版本

int height(struct TreeNode* root) {
    if (root == NULL) {
        return 0;
    } else {
        return fmax(height(root->left), height(root->right)) + 1;
    }
}

bool isBalanced(struct TreeNode* root) {
    if (root == NULL) {
        return true;
    } else {
        return fabs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
}

说明：在C语言中，我们使用了fmax函数来计算两个整数中的较大值，并且fabs函数用于计算绝对值。

Python3版本

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def height(root: TreeNode) -> int:
            if not root:
                return 0
            return max(height(root.left), height(root.right)) + 1

        if not root:
            return True
        return abs(height(root.left) - height(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

说明：在Python中，我们约定如果子树不平衡，则height函数返回-1，这样可以在isBalanced中直接利用返回值进行判断。

Golang版本

package main

import (
	"math"
)

func isBalanced(root *TreeNode) bool {
    if root == nil {
        return true
    }
    return abs(height(root.Left) - height(root.Right)) <= 1 && isBalanced(root.Left) && isBalanced(root.Right)
}

func height(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return max(height(root.Left), height(root.Right)) + 1
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

func abs(x int) int {
    if x < 0 {
        return -1 * x
    }
    return x
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/balanced-binary-tree/solutions/377216/ping-heng-er-cha-shu-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

说明：在Golang版本中，我们使用了一个辅助函数dfs来进行深度优先搜索，该函数返回子树的高度和是否平衡两个值。如果子树不平衡，则dfs返回-1和false。abs和max是辅助函数，分别用于计算绝对值和取两个整数中的较大值。

复杂度分析

• 时间复杂度
  时间复杂度为 O(n)，其中 n 是二叉树中的节点数。这是因为在递归的过程中，我们需要访问每一个节点来计算其左右子树的高度，并且对每个节点都要执行一次判断是否平衡的操作（比较高度差以及递归检查子树是否平衡）。每个节点最多被访问一次，因此总的时间复杂度是线性的。

• 空间复杂度
  空间复杂度取决于递归调用的深度，也就是树的深度。在最坏的情况下，当树完全不平衡时（例如每个节点都只有左子节点或右子节点），递归的深度会达到树的高度，也就是 O(n)。此时，递归调用栈需要存储 O(n) 个节点信息。

然而，在平均情况下，二叉树是平衡的，其深度通常是对数级别的，即 O(log n)。因此，在平均情况下，空间复杂度是 O(log n)。

但需要注意的是，空间复杂度并不只包括递归调用栈的开销，还包括系统为函数调用分配的其他资源（如局部变量等）。但在判断二叉树是否平衡的问题中，这些开销通常相对较小，可以忽略不计。

• 总结
  时间复杂度：O(n)
  空间复杂度（最坏情况）：O(n)
  空间复杂度（平均情况）：O(log n)
  其中，n 是二叉树中的节点数。

方法一：自顶向下递归（带后序遍历）

思路

方法一由于是自顶向下递归，因此对于同一个节点，函数 height 会被重复调用，导致时间复杂度较高。如果使用自底向上的做法，则对于每个节点，函数 height 只会被调用一次。

自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回 −1-1−1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。

方式二：带后序遍历的递归方法（自底向上）

思路

带后序遍历的递归方法（自底向上）在遍历到每个节点时，首先递归地检查其左右子树是否平衡，并返回子树的高度。如果子树不平衡（即高度差大于1），则立即返回-1表示不平衡，并向上传递这个信息。如果子树平衡，则返回其高度，继续向上传递。这样，在遍历到根节点时，就可以知道整棵树是否平衡。

代码实现

Java版本

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) != -1;
    }

    private int height(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftHeight = height(node.left);
        if (leftHeight == -1) {
            return -1;
        }
        int rightHeight = height(node.right);
        if (rightHeight == -1) {
            return -1;
        }
        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

说明：在Java版本中，isBalanced方法调用height方法来判断树是否平衡。height方法递归地计算每个节点的高度，并在发现不平衡时返回-1。

C语言版本

#include <limits.h>

typedef struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

int height(TreeNode* node) {
    if (node == NULL) {
        return 0;
    }
    int leftHeight = height(node->left);
    if (leftHeight == -1) {
        return -1;
    }
    int rightHeight = height(node->right);
    if (rightHeight == -1) {
        return -1;
    }
    if (abs(leftHeight - rightHeight) > 1) {
        return -1;
    }
    return MAX(leftHeight, rightHeight) + 1;
}

bool isBalanced(TreeNode* root) {
    return height(root) != -1;
}

说明：在C语言版本中，同样使用height函数来计算节点高度并判断平衡性。注意这里使用了limits.h中的INT_MIN来表示-1的整数类型（但在这个例子中我们直接返回-1），以及自定义的MAX宏来获取两个数中的较大值（或者可以使用#include <stdlib.h>中的max函数，如果存在的话）。

Python3版本

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def isBalanced(root):
    def height(node):
        if not node:
            return 0
        leftHeight = height(node.left)
        if leftHeight == -1:
            return -1
        rightHeight = height(node.right)
        if rightHeight == -1:
            return -1
        if abs(leftHeight - rightHeight) > 1:
            return -1
        return max(leftHeight, rightHeight) + 1
    
    return height(root) != -1

说明：在Python3版本中，我们定义了一个嵌套函数height来计算节点高度，并在isBalanced函数中调用它。Python中没有类型定义，所以我们直接使用类定义来创建树节点。

Golang版本

package main  
  
import (  
	"fmt"  
	"math"  
)  
  
type TreeNode struct {  
	Val   int  
	Left  *TreeNode  
	Right *TreeNode  
}  
  
func isBalanced(root *TreeNode) bool {  
	return height(root) != -1  
}  
  
func height(node *TreeNode) int {  
	if node == nil {  
		return 0  
	}  
	leftHeight := height(node.Left)  
	if leftHeight == -1 {  
		return -1  
	}  
	rightHeight := height(node.Right)  
	if rightHeight == -1 {  
		return -1  
	}  
	if math.Abs(float64(leftHeight-rightHeight)) > 1 {  
		return -1  
	}  
	return int(math.Max(float64(leftHeight), float64(rightHeight))) + 1  
}  
  

复杂度分析

• 时间复杂度：O(n)，其中n是二叉树中的节点数。每个节点最多被访问一次，因此总的时间复杂度是线性的。
• 空间复杂度：O(h)，其中h是二叉树的高度。这是由递归调用栈的深度决定的。在最坏的情况下（树完全不平衡），空间复杂度为O(n)。然而，在平均情况下，二叉树是平衡的，其高度通常是对数级别的，即O(log n)。但需要注意的是，这里的空间复杂度不包括可能由操作系统分配的系统

总结

针对上面提到的自顶向下递归（方式一）和自底向上递归（方式二）的二叉树平衡性检查方法，我们可以进行如下总结：

方式	优点	缺点	时间复杂度	空间复杂度
方式一（自顶向下递归）	直观易理解，直接根据定义判断	可能产生大量重复计算，效率较低	O(n)	O(h)（h为树的高度，最坏情况下为O(n)）
方式二（自底向上递归）	利用后序遍历减少重复计算，效率高	依赖于递归和高度差的比较，可能难以理解	O(n)	O(h)（h为树的高度，最坏情况下为O(n)）

注意：在方式二中，虽然空间复杂度在最坏情况下为O(n)，但这是因为递归调用栈的深度可能达到n。在平均情况下，对于平衡树，空间复杂度为O(log n)。

相似题目

以下是一些与判断二叉树平衡性相关的相似题目，它们涉及树的遍历、深度或高度的计算等概念：

相似题目	难度	链接
LeetCode 104 二叉树的最大深度	简单	LeetCode-104
LeetCode 110 平衡二叉树	简单	LeetCode-110
LeetCode 111 二叉树的最小深度	简单	LeetCode-111
LeetCode 543 二叉树的直径	简单	LeetCode-543
LeetCode 124 二叉树中的最大路径和	困难	LeetCode-124

这些题目都涉及到对二叉树的遍历和深度/高度的计算，可以通过递归或迭代的方式解决。其中，LeetCode 110题目与本文讨论的二叉树平衡性检查最为相似。