【 1. 线性卷积 】

• f(n) 的长度为 P，g(n) 的长度为 Q，则 $f(n)\ast g(n)$ 的长度为 L=P+Q-1。
  $$线性卷积：f(n)\ast g(n)=\sum _{k=0}^{L-1}f(k)g(n-k)=\sum _{k=0}^{L-1}g(k)f(n-k)=g(n)\ast f(n)$$

1.1 图解分析

• 假设 f(n) 和 g(n) 如下图所示：
  f(n)=[3,1,4,5]，n=0,1,2,3
  g(n)=[1,2,3]，n=0,1,2
  
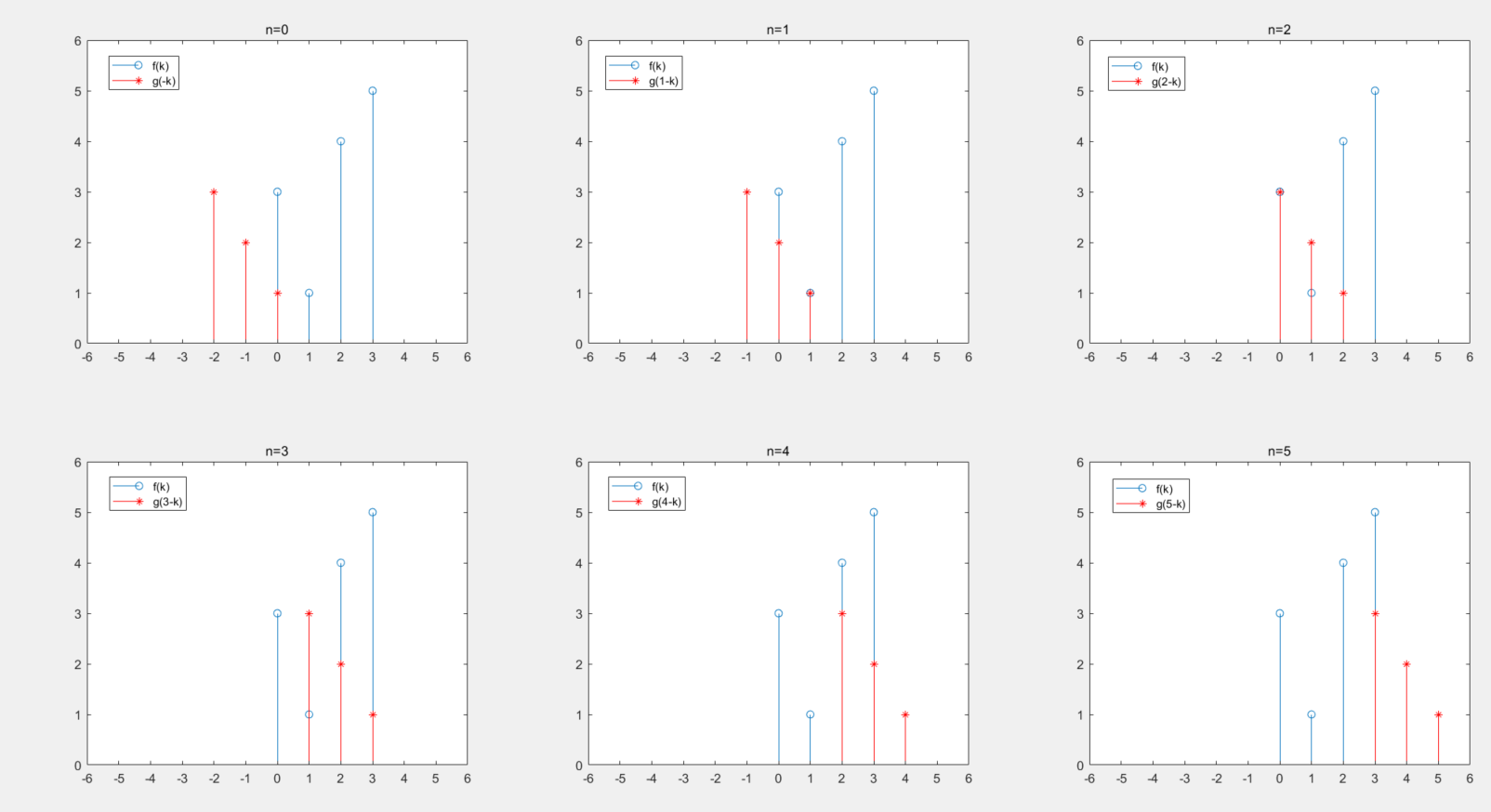
• 将 g(n) 和 h(n) 变换坐标为 g(k) 和 f(k)。 g(k) 翻转为 g(-k)，再向右滑动 n 变为 g(-(k-n))=g(n-k)，然后将对应相同位置的 g(n-k) 和 f(k) 相乘，最后将所有的乘积结果求和得到卷积结果 $g(n)\ast f(n)$。
  y(0)=1x3+2x0+3x0=3
  y(1)=1x1+2x3+3x0=7
  y(2)=1x4+2x1+3x3=15
  y(3)=1x5+2x4+3x1=16
  y(4)=1x0+2x5+3x4=22
  y(5)=1x0+2x0+3x5=15
  

1.2 矩阵相乘实现线性卷积

• 假设求信号 R（长度为P） 和信号 G（长度为Q） 的 线性卷积，则将两个信号都尾补零到长度 L（L=P+Q-1），然后按照如下矩阵相乘的方式进行线性卷积的运算。

$\{\begin{array}{cccc}{r}_1& 0& 0& \cdots \\ r_2& r_1& 0& \cdots \\ r_3& r_2& r_1& \cdots \\ ⋮& ⋮& ⋮& ⋮\\ r_L& r_{L-1}& \cdots & r_2\end{array}$