Deep Learning Part Five RNNLM的学习和评价-24.4.30

news2024/11/24 11:41:44

准备好RNNLM所需要的层，我们现在来实现RNNLM，并对其进行训练，然后再评价一下它的结果的。

5.5.1 RNNLM的实现

这里我们将RNNLM使用的网络实现为SimpleRnnlm类，其层结构如下：

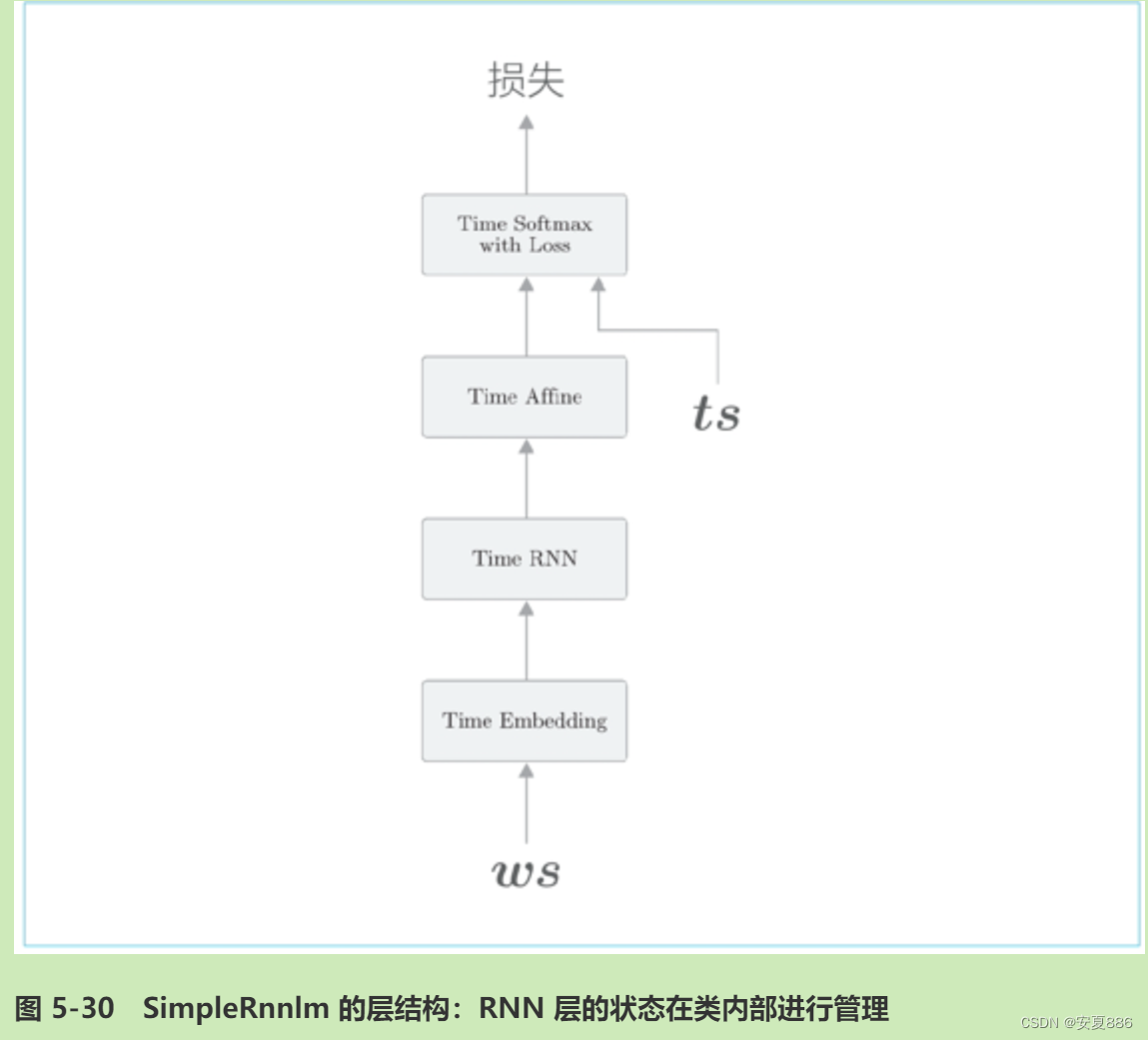
如图 5-30 所示，SimpleRnnlm 类是一个堆叠了 4 个 Time 层的神经网络。我们先来看一下初始化的代码:

import sys
sys.path.append('..')
import numpy as np
from common.time_layers import *

class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 初始化权重
        embed_W = (rn(V, D) / 100).astype('f')
        rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # 生成层
        self.layers = [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W, affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1]

        # 将所有的权重和梯度整理到列表中
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

拓展：

接着，我们来实现 forward() 方法、backward() 方法和 reset_state() 方法。

def forward(self, xs, ts):
    for layer in self.layers:
        xs = layer.forward(xs)
    loss = self.loss_layer.forward(xs, ts)
    return loss

def backward(self, dout=1):
    dout = self.loss_layer.backward(dout)
    for layer in reversed(self.layers):
        dout = layer.backward(dout)
    return dout

def reset_state(self):
    self.rnn_layer.reset_state()

从上述中，可以看出实现非常简单。在各个层中，正向传播和反向传播都正确地进行了实现。因此，我们只要以正确的顺序调用 forward()（或者 backward()）即可。方便起见，这里将重设网络状态的方法实现为 reset_state()。以上就是对 SimpleRnnlm 类的说明。

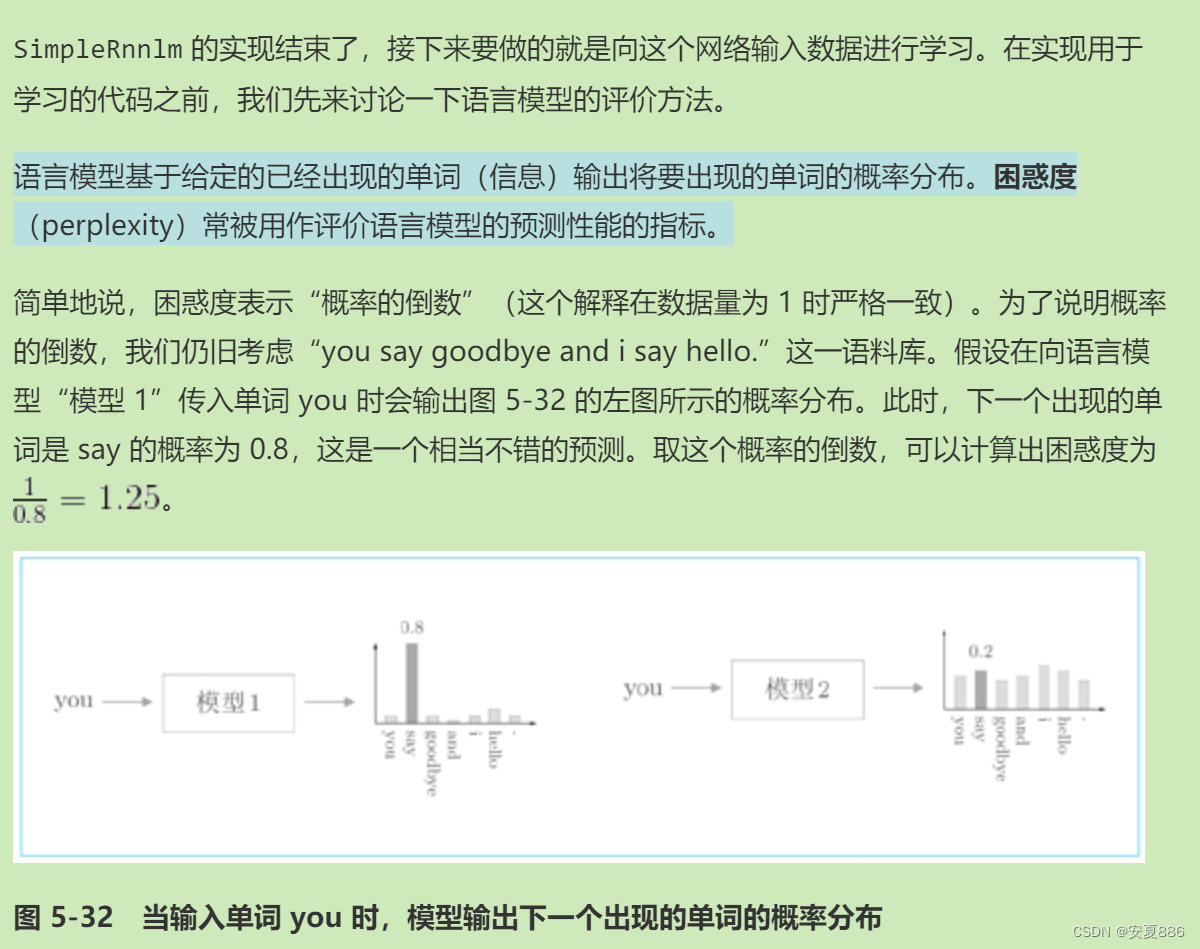
5.5.2　语言模型的评价

5.5.3 RNNLM的学习代码

下面，我们使用 PTB 数据集进行学习，不过这里仅使用 PTB 数据集（训练数据）的前 1000 个单词。这是因为在本节实现的 RNNLM 中，即便使用所有的训练数据，也得不出好的结果。下一章我们将对它进行改进。

import sys
sys.path.append('..')
import matplotlib.pyplot as plt
import numpy as np
from common.optimizer import SGD
from dataset import ptb
from simple_rnnlm import SimpleRnnlm


# 设定超参数
batch_size = 10
wordvec_size = 100
hidden_size = 100 # RNN的隐藏状态向量的元素个数
time_size = 5 # Truncated BPTT的时间跨度大小
lr = 0.1
max_epoch = 100

# 读入训练数据（缩小了数据集）
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)

xs = corpus[:-1] # 输入
ts = corpus[1:] # 输出（监督标签）
data_size = len(xs)
print('corpus size: %d, vocabulary size: %d' % (corpus_size, vocab_size))

# 学习用的参数
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []

# 生成模型
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)

# ❶ 计算读入mini-batch的各笔样本数据的开始位置
jump = (corpus_size - 1) // batch_size
offsets = [i * jump for i in range(batch_size)]

for epoch in range(max_epoch):
    for iter in range(max_iters):
        # ❷ 获取mini-batch
        batch_x = np.empty((batch_size, time_size), dtype='i')
        batch_t = np.empty((batch_size, time_size), dtype='i')
        for t in range(time_size):
            for i, offset in enumerate(offsets):
                batch_x[i, t] = xs[(offset + time_idx) % data_size]
                batch_t[i, t] = ts[(offset + time_idx) % data_size]
            time_idx += 1

        # 计算梯度，更新参数
        loss = model.forward(batch_x, batch_t)
        model.backward()
        optimizer.update(model.params, model.grads)
        total_loss += loss
        loss_count += 1

    # ❸ 各个epoch的困惑度评价
    ppl = np.exp(total_loss / loss_count)
    print('| epoch %d | perplexity %.2f'
          % (epoch+1, ppl))
    ppl_list.append(float(ppl))
    total_loss, loss_count = 0, 0

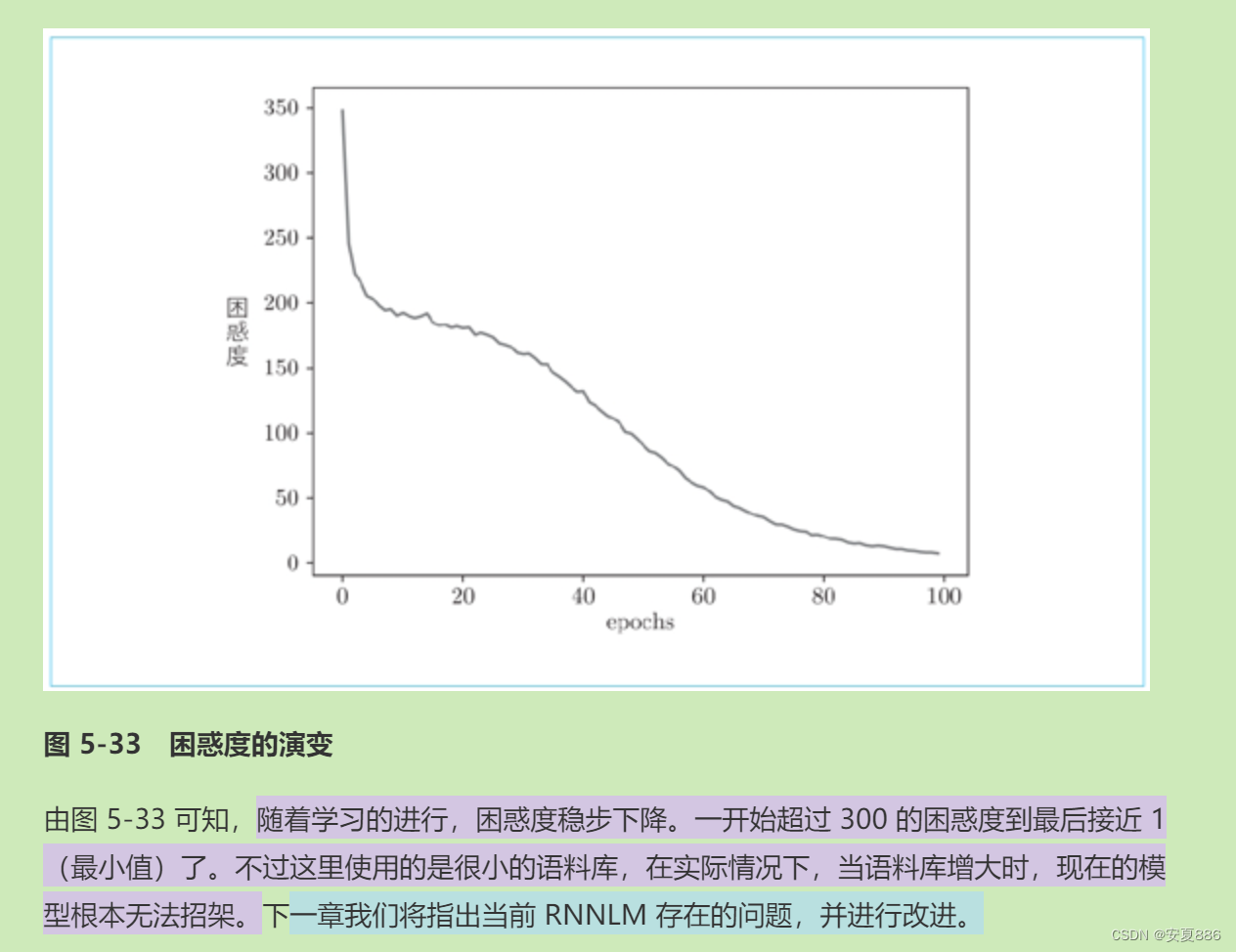
5.5.4　RNNLM 的 Trainer 类

只摘录了核心：

...
from common.trainer import RnnlmTrainer

...
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)

trainer.fit(xs, ts, max_epoch, batch_size, time_size)

如上所示，首先使用 model 和 optimizer 初始化 RnnlmTrainer 类，然后调用 fit()，完成学习。此时，RnnlmTrainer 类的内部将执行上一节进行的一系列操作，具体如下所示。

按顺序生成 mini-batch
调用模型的正向传播和反向传播
使用优化器更新权重
评价困惑度

使用Trainer的好处：

使用 RnnlmTrainer 类，可以避免每次写重复的代码。本书的剩余部分都将使用 RnnlmTrainer 类学习 RNNLM。

5.6 小结

本章的主题是 RNN。RNN 通过数据的循环，从过去继承数据并传递到现在和未来。如此，RNN 层的内部获得了记忆隐藏状态的能力。本书中我们花了很多时间说明 RNN 层的结构，并实现了 RNN 层（和 Time RNN 层）。

本章还利用 RNN 创建了语言模型。语言模型给单词序列赋概率值。特别地，条件语言模型从已经出现的单词序列计算下一个将要出现的单词的概率。通过构成利用了 RNN 的神经网络，理论上无论多么长的时序数据，都可以将它的重要信息记录在 RNN 的隐藏状态中。但是，在实际问题中，这样一来，许多情况下学习将无法顺利进行。下一章我们将指出 RNN 存在的问题，并研究替代 RNN 的 LSTM 层或 GRU 层。这些层在处理时序数据方面非常重要，被广泛用于前沿研究。

本章所学的内容

RNN 具有环路，因此可以在内部记忆隐藏状态
通过展开 RNN 的循环，可以将其解释为多个 RNN 层连接起来的神经网络，可以通过常规的误差反向传播法进行学习（= BPTT）
在学习长时序数据时，要生成长度适中的数据块，进行以块为单位的 BPTT 学习（= Truncated BPTT）
Truncated BPTT 只截断反向传播的连接
在 Truncated BPTT 中，为了维持正向传播的连接，需要按顺序输入数据
语言模型将单词序列解释为概率
理论上，使用 RNN 层的条件语言模型可以记忆所有已出现单词的信息