欢迎来CILMY23的博客
本篇主题为 贪心算法:零钱兑换的奇妙之旅
个人主页:CILMY23-CSDN博客
个人专栏: Python | C++ | C语言 | 数据结构与算法
上一篇C++博客:掌握C++函数重载和引用开启代码优化的新篇章
感谢观看,支持的可以给个一键三连,点赞评论+收藏。
一、贪心算法介绍
贪心算法(greedy algorithm,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
贪心算法我们也说它是一个贪心策略,贪心策略是一种简单、高效的求解最优化问题的策略,通过局部最优选择来寻找整体的最优选择。
贪心算法的步骤:
我们通常会把问题拆解分成很多步,解决每一步的时候,我们都会追求每一步的“最优”解法,然后通过每一步的解法,我们希望得到全局的最优解。
二、贪心算法应用
应用一、零钱找零问题
假设我们有46块钱,现在的金钱面额有20元的,10元的,5元的,1元的。如何用最少的张数凑够46块钱,那所以我们凑零钱肯定是先从20块的开始找,然后找到1块钱的。这就是贪心策略,在选择钱的时候,我们总会选择当前的最优选择。

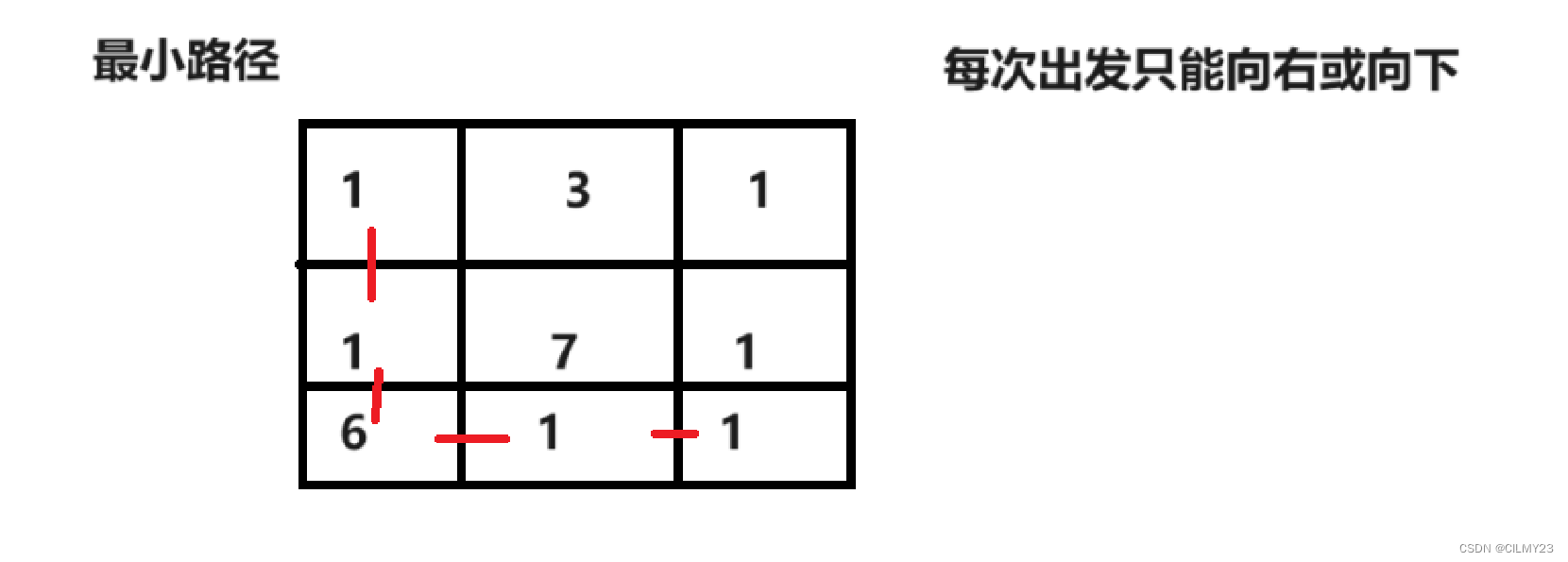
应用二、最小路径和
我们需要找最小路径,从左上角走到右下角,我们只能向右或向下,当我们走第一步的时候,只能在1和3选择,我们选择1向下,然后我们从6和7才选到这个6,这就是贪心策略。但是当我们走到底的时候未必是全局最优解,按照目前的贪心策略得到的结果是10。
应用三、背包问题
假设现在有三个物品1,2,3,背包中有一个容量,最大体积是9,如果只按照体积来看,我们会选择装最多的3号物品,装了九个3号物品。如果只考虑价值,我们会装了一个物品1,和2个物品 3. 这就是贪心策略的应用,在解决问题的时候,只考虑每步的“最优”选择。当然,这题我们也可以考虑单位体积的价值。

三、贪心算法的特点
3.1 贪心策略的提出
- 贪心策略的提出是没有标准和模板的
- 可能每一道题的贪心策略都是不同的
3.2 贪心策略的正确性
因为有可能在局部推算最优解的时候,贪心策略是一个“错误”的方法,正确的贪心策略我们是需要“证明”的。证明它是错的只需要一个反例,但是证明它是正确的,我们所采用的证明方法:范围是数学中所有的证明方法
证明 零钱找零 贪心策略是最优解:
如何用最少的张数换到零钱?
假设我们现在做最优解的选择,20面额的有A张,10块钱的有B张,5块钱的有C张,1块钱的有D张。当其余面额都满足上一张面值的时候,我们就会对其进行兑换。所以两张五块的我们就会换成一张十块的。我们按照这样去推测最优解,最终得到A可以有n张,B小于等于1张,C也小于等于1张,D小于等于4张。
然后我们看贪心策略 20面额的有a张,10块钱的有b张,5块钱的有c张,1块钱的有d张,而在贪心策略中,我们是能用a就用a,用不了a才用b,所以其余的张数绝对是符合,b小于等于1张,c也小于等于1张,d小于等于4张这个条件的,也因此a绝对不可能大于A,同理,b也不可能大于B,c不可能大于C,d不可能大于D。

感谢各位同伴的支持,本期贪心算法篇就讲解到这啦,如果你觉得写的不错的话,可以给个一键三连,点赞关注+收藏,若有不足,欢迎各位在评论区讨论。