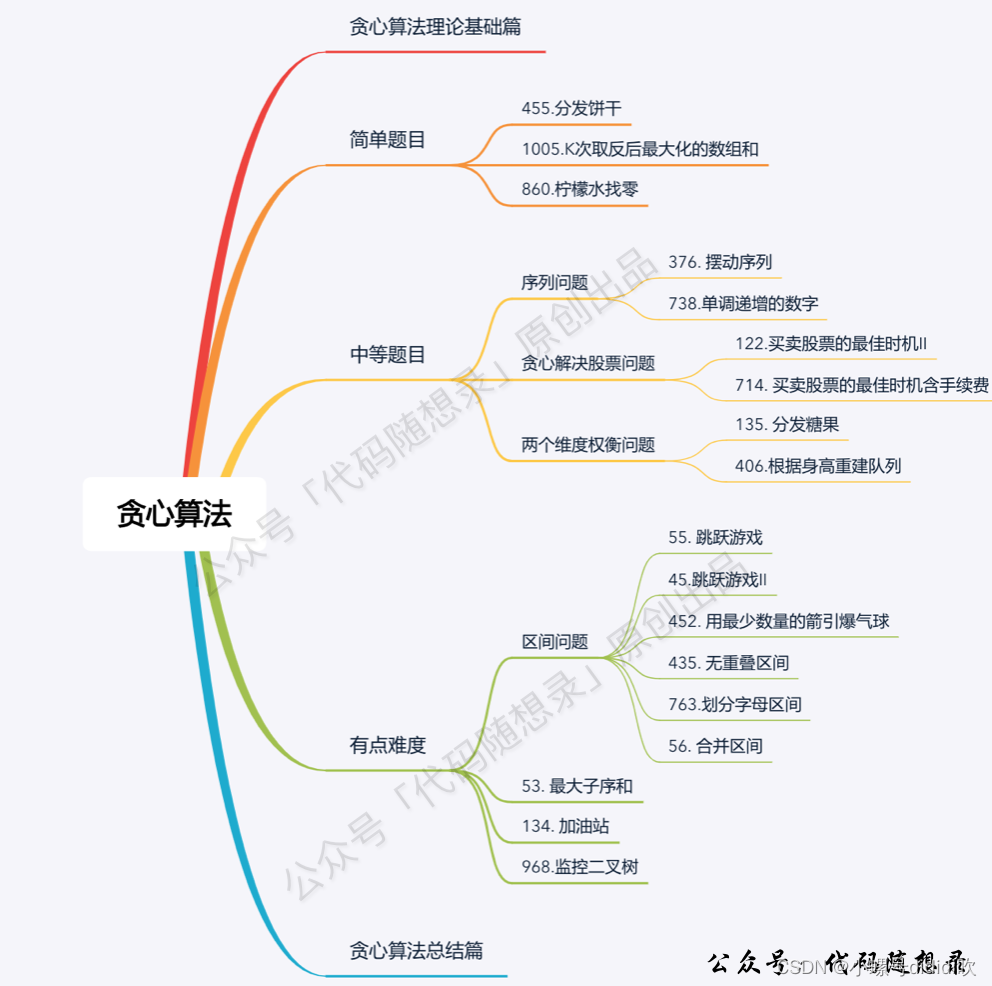
目录
理论基础
一、简单贪心
LeetCode455:分发饼干
二、中等贪心
2.1 序列问题
LeetCode376:摆动序列
2.2 贪心股票问题
LeetCode121:买卖股票的最佳时机
LeetCode121:买卖股票的最佳时机ii
2.3 两个维度权衡问题
LeetCode135:分发糖果
三、较难问题
区间问题
LeetCode55:跳跃游戏i
LeetCode55:跳跃游戏ii
LeetCode452:用最少数量的箭引爆气球
LeetCode435:无重叠区间
LeetCode763:划分字母区间
LeetCode56:合并区间
其他
LeetCode53:最大子序和
贪心算法其实就是没有什么规律可言,所以大家了解贪心算法 就了解它没有规律的本质就够了。 不用花心思去研究其规律, 没有思路就立刻看题解。基本贪心的题目 有两个极端,要不就是特简单,要不就是死活想不出来。
学完贪心之后再去看动态规划,就会了解贪心和动规的区别。
理论基础
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
举例:有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿?指定每次拿最大的,最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。
再举一个例子如果是 有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
什么时候用贪心呢?没有固定的套路。刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
一、简单贪心
LeetCode455:分发饼干
思路:这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,
全局最优就是喂饱尽可能多的小孩。
所以可以尝试使用贪心策略,先将饼干数组和小孩数组排序。然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。

class Solution {
// 思路:优先考虑胃口,先喂饱大胃口
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int start = s.length - 1;
// 遍历胃口
for (int index = g.length - 1; index >= 0; index--) {
if(start >= 0 && g[index] <= s[start]) {
start--;
count++;
}
}
return count;
}
}二、中等贪心
2.1 序列问题
LeetCode376:摆动序列
思路:局部最优是删除连续坡度上的节点,保证这个坡度有两个局部峰值
整体最优是整个序列拥有最多的局部峰值
在实际操作上,实际连删除都不用做,只需添加数组的局部峰值即可
本题的难度在于要考虑多种情况:(curdiff代表后一个坡度,prediff代表前一个坡度)
即单调有平坡、上下中间有平坡和只有两个数的情况,具体分析见代码随想录
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) {
return nums.length;
}
//当前差值
int curDiff = 0;
//上一个差值
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
//得到当前差值
curDiff = nums[i] - nums[i - 1];
//如果当前差值和上一个差值为一正一负
//等于0的情况表示初始时的preDiff
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
}这道题还可以用动态规划来做,这里就不讲了。之后可以试着做一做。
2.2 贪心股票问题
LeetCode121:买卖股票的最佳时机
思路:局部最优即左界最小,在局部最优的基础上要求的全局最优即右界最大,也就是差值最大。
class Solution {
public int maxProfit(int[] prices) {
int max = 0;
int low = Integer.MAX_VALUE; //保留左侧最小值
for (int i = 0; i < prices.length; i++) {
low = Math.min(low, prices[i]); // 取最左最小价格,确定左界
max = Math.max(max, prices[i] - low); // 寻找右侧最大值
}
return max;
}
}LeetCode121:买卖股票的最佳时机ii
思路:局部最优即在区间中寻找所有的最大递增子区间,且子区间之间不能重叠
整体最优:取所有最大的递增子区间,最后利润和也最大。
由于最后只要求利润,该题可以变成只要收集每天的正利润,而无需考虑区间的左右界。
// 贪心思路
class Solution {
public int maxProfit(int[] prices) {
int result = 0;
for (int i = 1; i < prices.length; i++) {
result += Math.max(prices[i] - prices[i - 1], 0);
}
return result;
}
}2.3 两个维度权衡问题
LeetCode135:分发糖果
思路:本题需要先确定一遍后,在确定另一边,从左到右的局部最优即:只要右边评分比左边大,右边的孩子就多一个糖果。全局最优:评分高的右边孩子比左边孩子糖果更多。
本题需要先从左到右更新,再从右到左,这样才能满足相邻条件。从右到左局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
class Solution {
/**
分两个阶段
1、起点下标1 从左往右,只要 右边 比 左边 大,右边的糖果=左边 + 1,不大于就取最小糖果数1;
2、起点下标 ratings.length - 2 从右往左, 只要左边 比 右边 大,此时 左边的糖果应该 取本身的糖果数(符合比它左边大) 和 右边糖果数 + 1 二者的最大值,这样才符合 它比它左边的大,也比它右边大
*/
public int candy(int[] ratings) {
int len = ratings.length;
int[] candyVec = new int[len];
candyVec[0] = 1;
for (int i = 1; i < len; i++) {
candyVec[i] = (ratings[i] > ratings[i - 1]) ? candyVec[i - 1] + 1 : 1;
}
for (int i = len - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
}
}
int ans = 0;
for (int num : candyVec) {
ans += num;
}
return ans;
}
}三、较难问题
区间问题
LeetCode55:跳跃游戏i
思路:总共要跳nums.length-1步才能到达终点,局部解即取最大跳跃步数max,每次循环以第一轮的max为起点再次计算max的覆盖范围
整体解即所有的最大跳跃步数范围是否能覆盖到终点。
class Solution {
public boolean canJump(int[] nums) {
int max = 0;
for(int i=0;i<=max;i++){ //这里注意是小于等于max,max更新等于以新一轮覆盖点为起点再次覆盖
max = Math.max(i+nums[i],max);
if(max>=nums.length-1) return true;
}
return false;
}
}LeetCode55:跳跃游戏ii
思路:局部解即每次的跳转步数尽可能最大,这样跳跃次数就最小
整体解即范围覆盖到终点且跳跃次数最小
本题的关键在于什么时候对步数进行+1?用到两个变量curIndex和preIndex来确定位置
class Solution {
public int jump(int[] nums) {
int nextIndex = 0;
int curIndex = 0;
int count = 0;
for(int i=0; i<=nums.length;i++){
nextIndex = Math.max(nextIndex,i+nums[i]);
if(i == curIndex){ //当走到当前的最大覆盖范围时,判断是否到终点
count++; //如果没到,就要跳一步
curIndex = nextIndex; //跳到更新过的下一坐标
if(nextIndex >= nums.length - 1) break; //如果到了则走完了
}
}
return count;
}
}LeetCode452:用最少数量的箭引爆气球
思路:写了435,这道题就很容易了
class Solution {
public int findMinArrowShots(int[][] points) {
int count = 1;
Arrays.sort(points, (x,y)->Integer.compare(x[1],y[1]));
int end = points[0][1];
for(int i=1;i<points.length;i++){
//只要右界排序,记录不重叠的情况就可以了,每次不重叠就需要多一支箭
if(end < points[i][0]){
count++;
end = points[i][1];
}
}
return count;
}
}LeetCode435:无重叠区间
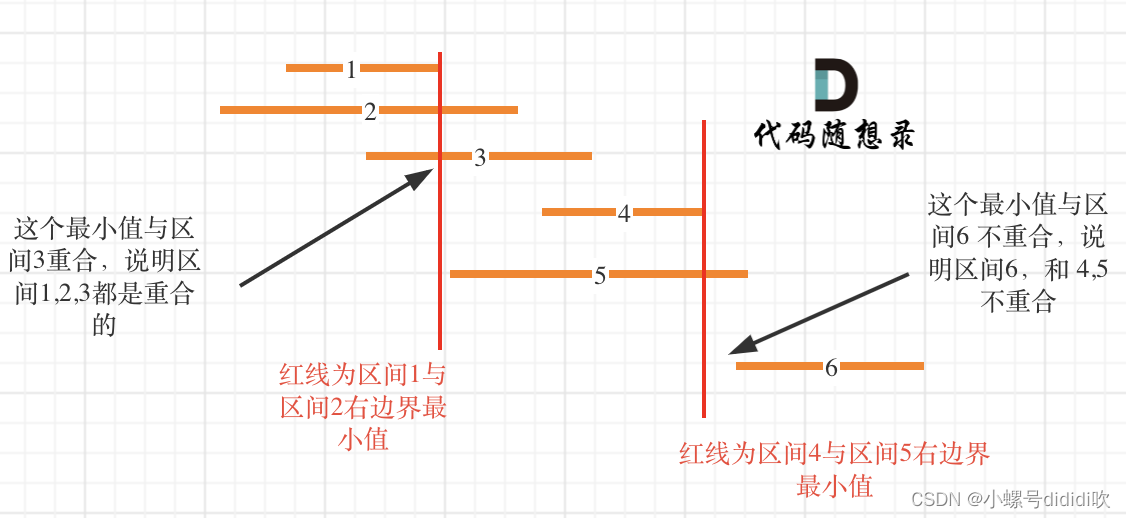
思路:重叠区间问题通常有两种思路:要么是按左边界排序,要么是按右边界
1. 按右边界升序排列,从左向右可以记录非重叠区间的个数,总数-非重叠个数=重叠个数
非重叠只要判断end和上一区间的左区间的关系
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a,b)-> {
return Integer.compare(a[1],b[1]);
});
int count = 1; //记录非重叠区间的个数
int end = intervals[0][1];
for(int i = 1;i < intervals.length;i++){
if(end <= intervals[i][0]){ //无重叠区间,count++,更新end
count++;
end = intervals[i][1];
}
}
return intervals.length-count;
}
}2. 按左边界升序排序,向左到右可以记录重叠的区间个数,直接得到重叠个数就是移除个数
非重叠和重叠都要更新end,之所以count取end和右界的较小值是因为,可能会出现>=3个区间重叠的情况。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a,b)-> {
return Integer.compare(a[0],b[0]);
});
int count = 0; //记录重叠区间的个数
int end = intervals[0][1];
for(int i = 1;i < intervals.length;i++){
if(end <= intervals[i][0]){ //无重叠区间,更新end
end = intervals[i][1];
}else{
count++;
end = Math.min(end, intervals[i][1]); //重叠区间的end
}
}
return count;
}
}LeetCode763:划分字母区间
思路:首先遍历计算每个字母的最后出现下标,然后从头开始遍历,并更新最远出现下标,当到达最后序号时进行一次分割
class Solution {
public List<Integer> partitionLabels(String s) {
List<Integer> list = new ArrayList<>();
int[] record = new int[26];
//首先记录字母最后一次出现的下标
for(int i=0;i<s.length();i++){
record[s.charAt(i)-'a'] = i;
}
int idx = 0;
int last = -1;
//然后当遍历下标等于最后一次的下标时,添加字符串长度
for(int i=0;i<s.length();i++){
idx = Math.max(idx, record[s.charAt(i)-'a']);
if(i == idx){
list.add(idx-last); //先添加结果到list,再更新
last = idx;
}
}
return list;
}
}LeetCode56:合并区间
思路:同样首先按照左边界先排序,然后判断左边界和最右边界
(记得判断=到底属于那种情况)
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new LinkedList<>();
Arrays.sort(intervals, (x,y)->Integer.compare(x[0],y[0]));
int left = intervals[0][0];
int right = intervals[0][1];
for(int i = 1; i<intervals.length; i++){
if(right >= intervals[i][0]){ //重叠,合并
right = Math.max(right, intervals[i][1]);
}else{ //不重叠,添加旧区间,更新left、right
res.add(new int[]{left, right});
left = intervals[i][0];
right = intervals[i][1];
}
}
res.add(new int[]{left, right});
return res.toArray(new int[res.size()][2]);
}
}其他
LeetCode53:最大子序和
思路:连续子数组局部最优,即遇到连续和count为负数,则立刻放弃当前count,置0,相当于从当前位置重新开始计算连续子数组和。整体最优即用sum来计算循环中count的最大值。
class Solution {
public int maxSubArray(int[] nums) {
if (nums.length == 1){
return nums[0];
}
int sum = Integer.MIN_VALUE;
int count = 0;
for (int i = 0; i < nums.length; i++){
count += nums[i];
sum = Math.max(sum, count); // 取区间累计的最大值(相当于不断确定最大子序终止位置)
if (count <= 0){
count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
}
return sum;
}
}