在当今这个数据驱动的时代,机器学习以其强大的学习和预测能力,成为了推动科技进步的重要力量。而在机器学习的背后,数学原理,尤其是导数的应用,为其提供了坚实的理论支撑。本文将详细探讨导数在机器学习中的体现,揭开其背后的微变奥秘。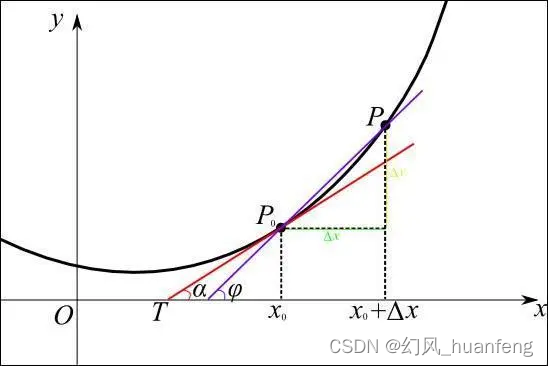
一、导数的概念及其在机器学习中的作用
导数,作为微积分学中的核心概念,描述了函数在某一点的切线斜率,即函数值随自变量变化的快慢程度。在机器学习中,导数被广泛应用于优化算法、损失函数、梯度下降等多个方面,为模型的学习和调整提供了重要的数学工具。
- 优化算法中的导数
机器学习模型的训练过程本质上是一个优化问题,即寻找一组参数使得模型在训练数据上的性能达到最优。这通常通过定义一个损失函数来衡量模型的预测误差,并使用优化算法来不断调整参数,使得损失函数值逐渐减小。而优化算法的关键就在于利用导数信息来指导参数的更新方向。
例如,在梯度下降算法中,我们通过计算损失函数关于模型参数的梯度(即导数向量)来确定参数更新的方向。具体来说,梯度下降算法会沿着损失函数值下降最快的方向(即负梯度方向)来更新参数,从而逐步减小损失函数值。这种基于导数信息的优化方法使得机器学习模型能够高效地找到最优解。
- 损失函数中的导数
损失函数是机器学习中用于衡量模型预测误差的函数。不同的损失函数对应着不同的误差度量方式,如均方误差、交叉熵误差等。而在实际应用中,我们通常选择那些易于计算导数的损失函数,以便在优化过程中能够高效地计算梯度信息。
例如,在线性回归问题中,我们通常使用均方误差作为损失函数。均方误差函数关于模型参数的导数易于计算,且具有良好的数学性质(如凸性等),这使得梯度下降算法能够快速地收敛到最优解。而在分类问题中,交叉熵误差则是一个常用的损失函数。通过计算交叉熵误差关于模型参数的导数,我们可以得到每个类别的预测概率与真实标签之间的差异程度,从而指导模型进行参数更新。
二、导数在机器学习中的具体应用
在机器学习的各个领域中,导数都发挥着不可或缺的作用。下面我们将从神经网络、支持向量机、决策树等方面来介绍导数在机器学习中的具体应用。
- 神经网络中的反向传播算法
神经网络是机器学习中最具代表性的模型之一。在神经网络的训练过程中,反向传播算法是一个至关重要的步骤。该算法通过计算损失函数关于网络参数的梯度来指导参数的更新方向。具体来说,反向传播算法首先通过前向传播计算网络在每个节点的输出值以及最终的损失函数值;然后利用链式法则逐层计算损失函数关于网络参数的梯度;最后根据梯度信息更新网络参数以减小损失函数值。这种基于导数信息的优化方法使得神经网络能够自动地调整其内部结构以适应不同的任务需求。
- 支持向量机中的核函数与梯度下降
支持向量机是一种广泛应用于分类问题的机器学习算法。在支持向量机中,核函数被用于将原始数据映射到高维空间以增加数据的可分性。而核函数的选择则直接影响到支持向量机的性能。为了选择合适的核函数参数以及支持向量机的其他超参数(如惩罚项系数等),我们可以使用梯度下降等优化算法来最小化损失函数值。通过计算损失函数关于超参数的梯度并更新超参数值以减小损失函数值我们可以得到一组最优的超参数配置使得支持向量机在训练数据上达到最优的性能表现。
- 决策树中的信息增益与梯度提升决策树
决策树是一种基于树形结构的机器学习模型它通过递归地选择最优特征进行划分来构建一棵树形结构以实现分类或回归任务在决策树的构建过程中信息增益是一个重要的评价指标它衡量了使用某个特征进行划分后能够减少的不纯度(即分类误差或回归误差)的程度信息增益越大说明使用该特征进行划分后能够获得的分类或回归效果越好因此我们应该选择信息增益最大的特征进行划分在决策树的构建过程中我们也可以利用导数信息来指导特征的选择和划分点的确定例如通过计算损失函数关于特征值的梯度来确定最佳的划分点或者使用梯度提升决策树等算法来进一步提高模型的性能表现。