目录
1.课题概述
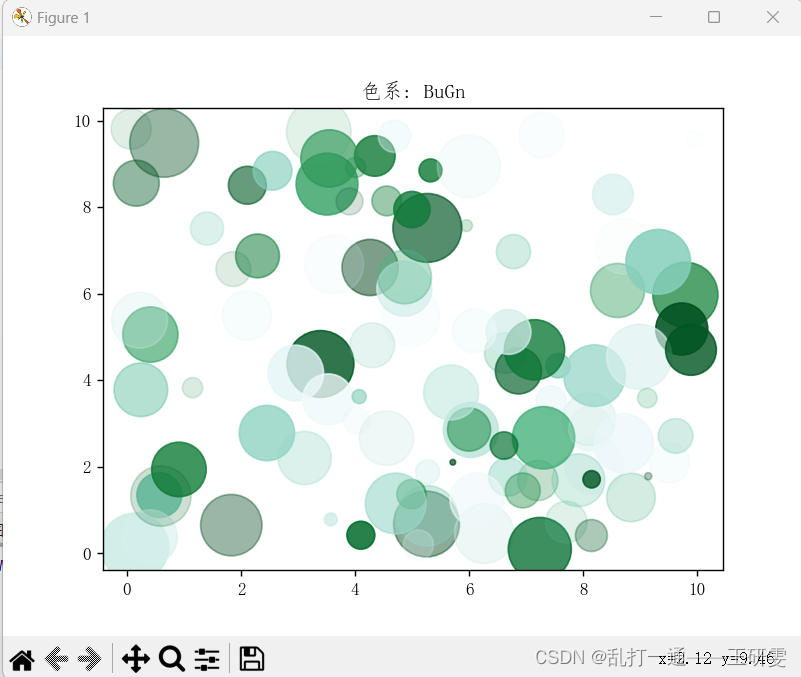
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
4.1 粒子滤波器基础
4.2 电池剩余使用寿命建模与预测
4.3 粒子滤波器在电池寿命预测中的应用
5.完整工程文件
1.课题概述
基于粒子滤波器的电池剩余使用寿命计算。根据已知的数据,预测未来的数据。
2.系统仿真结果



3.核心程序与模型
版本:MATLAB2022a
............................................................
%开始粒子滤波过程
for k=2:N
% 状态转移方程
for i=1:M
% 使用连续时间状态方程更新粒子
Xnoise(1,i,k)=Xnoise(1,i,k-1)*exp(Xnoise(2,i,k-1)*(k-(k-1)))+sqrt(Xvar)*randn();
Xnoise(2,i,k)=Xnoise(2,i,k-1)+sqrt(Bvar)*randn();
end
% 更新粒子示例矩阵以便绘制
if mod(k,25)==0 && k<=begin
ind = size(Xidx,2);
Xc(:,ind+1) = (datasample(Xnoise(1,:,k),10))';
Xidx(:,ind+1) = k;
end
% 计算粒子权重
for i=1:M
% 使用观测模型计算期望测量值
Znoise(1,i,k) = Xnoise(1,i,k)+ Zstd*randn(); % 加上测量噪声
Weight(k,i) = exp(-(Ym(1,k)-Znoise(1,i,k))^2/2/R)+1e-99; % 计算每个粒子的权重
end
end
Xs = Xnoise(1,:,1);
Bs = Xnoise(2,:,1);
Xvar = 0.1;
Bvar = 1e-10;
x_initial = X0(1);
b_initial = X0(2);
for l=1:length(Xs)
x_pdf(l)=normpdf(Xs(l),x_initial,sqrt(Xvar));
end
for l=1:length(Bs)
b_pdf(l)=normpdf(Bs(l),b_initial,sqrt(Bvar));
end
figure;
subplot(121);
plot(Xs,x_pdf,'b.');
xlabel('x');
ylabel('概率分布');
subplot(122);
plot(Bs,b_pdf,'b.');
xlabel('b');
ylabel('概率分布');
48
4.系统原理简介
在电池管理系统(Battery Management System, BMS)中,预测电池的剩余使用寿命(Remaining Useful Life, RUL)是一项重要的任务,而粒子滤波器作为一种有效的概率状态估计方法,在此领域得到了广泛应用。粒子滤波器利用蒙特卡洛方法模拟随机过程,能够处理非线性和非高斯问题,特别适用于复杂动力学系统的状态估计,例如锂离子电池老化模型。
4.1 粒子滤波器基础
粒子滤波器是一种递推贝叶斯估计方法,它通过一组随机样本(称为粒子)及其对应的权重来近似后验概率分布。每个粒子代表系统的一个潜在状态,权重反映了该状态出现的可能性。粒子滤波器主要包括两个核心步骤:预测和更新。

4.2 电池剩余使用寿命建模与预测
电池的健康状态(State of Health, SOH)通常被定义为其初始容量与当前容量的比值,用于表征电池的衰退程度。电池剩余使用寿命可以通过电池SOH的变化趋势进行预测。
假设我们有一个反映电池老化的非线性动力学模型:
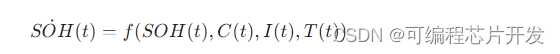
其中,SOH(t) 表示时间 t 时的电池健康状态,C(t) 是电池的荷电状态,I(t) 是充电/放电电流,T(t) 是环境温度等影响因素。
通过粒子滤波器估计出的连续SOH序列,可以结合经验阈值或者基于寿命曲线拟合的方法,计算出电池预计达到某个终止SOH(如80%)的时间,从而得到剩余使用寿命:
4.3 粒子滤波器在电池寿命预测中的应用
-
状态空间模型构建 设计适合电池衰减过程的动力学模型,并建立观测模型以从测量数据中提取与SOH相关的信息。
-
初始化粒子集 随机生成一组代表初始SOH状态的粒子。
-
循环执行预测与更新 每个时间步,根据电池的实际运行条件和模型,对粒子进行预测并更新其权重;随后进行重采样以保持粒子的有效性和多样性。
-
RUL预测 根据估计出的SOH随时间演变的趋势,预测未来某时刻的SOH值,并据此计算剩余使用寿命。
5.完整工程文件
v