写在前面

本专栏专注于分析与讲解【面试经典150】算法，两到三天更新一篇文章，欢迎催更……

专栏内容以分析题目为主，并附带一些对于本题涉及到的数据结构等内容进行回顾与总结，文章结构大致如下，部分内容会有增删：

• Tag：介绍本题牵涉到的知识点、数据结构；
• 题目来源：贴上题目的链接，方便大家查找题目并完成练习；
• 题目解读：复述题目（确保自己真的理解题目意思），并强调一些题目重点信息；
• 解题思路：介绍一些解题思路，每种解题思路包括思路讲解、实现代码以及复杂度分析；
• 知识回忆：针对今天介绍的题目中的重点内容、数据结构进行回顾总结。

---

Tag

【二叉搜索树】【建树】

---

题目来源

108. 将有序数组转换为二叉搜索树

---

解题思路

给定一个二叉搜索树的中序遍历结果，是否可以唯一地确定二叉搜索树呢？答案是否定的。因为没有其他的条件限制，每一个节点都可以作为二叉搜索树的根节点，所以可能的二叉搜索树会有好多个。

如果增加一个要求二叉搜索树高度平衡（左、右子树的高度差不超过 1）的限制条件，是否可以唯一地确定二叉搜索树？依然无法确定。比如二叉搜索树的中序遍历结果为 [-10, -3, 0, 5, 9]，对应的二叉搜索树有如下几种可能：

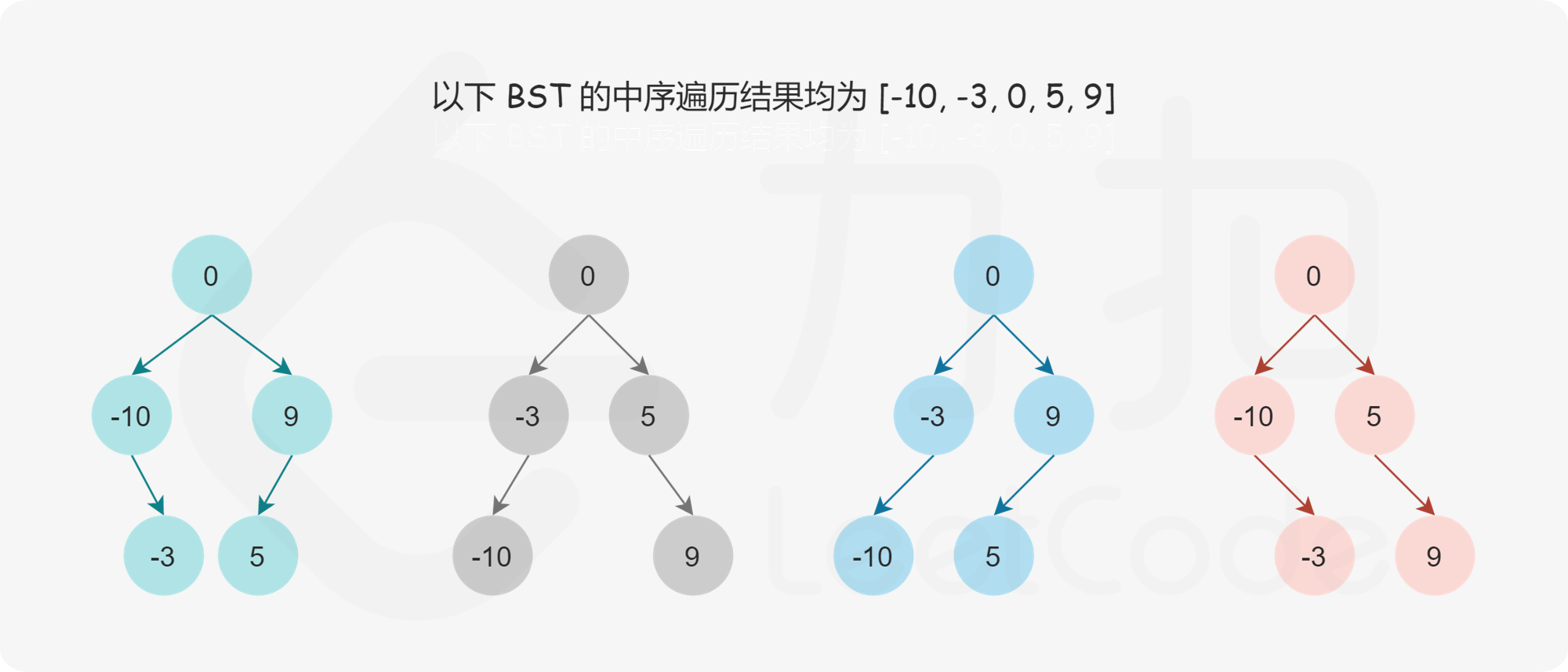
虽然增加了一个限制条件，但是根据数组转换成的二叉搜索树仍不唯一，但是根据高度平衡的限制，二叉搜索树的根节点必须选择数组的中间节点。数组长度为奇数的话直接选择数组最中间的节点作为二叉搜索树的根节点。数组长度为偶数的话可以选择中间位置的左边数字或者右边数字作为二叉搜索树的根节点。

偶数情况为什么可以二选一？因为题目要求是平衡二叉搜索树，即只要求左右子树的高度差不超过 1 就行。偶数情况的二选一就是让左右子树的高度差为 1，如此转化成的二叉搜索树是有效的平衡树。

确定平衡二叉搜索树的根节点之后，其余的数字分别位于平衡二叉搜索树的左子树和右子树中，左子树和右子树分别也是平衡二叉搜索树，因此可以通过递归的方式创建平衡二叉搜索树。

根据选择数组中的哪一个节点作为根节点，此题有三种解题策略：

• 中序遍历，总是选择中间位置左边的数字作为根节点
• 中序遍历，总是选择中间位置右边的数字作为根节点
• 中序遍历，选择任意一个中间位置数字作为根节点

三种解题策略代码实现过程几乎一致，只有一点点的不同。

方法一：中序遍历递归建树

以下第一种解题策略的实现代码，将 ① 处代码分别替换为 ②、③ 处代码即可实现第二、三中解题代码。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    TreeNode* helper(vector<int>& nums, int left, int right){
        if(left > right){
            return nullptr;
        }

        int mid = (left + right) >> 1;              // ①
        /*
        int mid = (left + right + 1) >> 1;          // ②
        int mid = (left + right + rand() % 2) >> 1; // ③
        */
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid-1);
        root->right = helper(nums, mid+1, right);
        return root;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1);
    }
};

复杂度分析

时间复杂度：$O(n)$，$n$ 是数组 nums 的长度，数组中的每个数字只会访问一次。

空间复杂度：$O(logn)$。空间复杂度主要取决于递归站的深度。

---

写在最后

如果您发现文章有任何错误或者对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度的方法，欢迎评论区交流。

最后，感谢您的阅读，如果有所收获的话可以给我点一个 👍 哦。